Draw and discuss the graph of f(x)=x2/3−x4/3
Video Solution
Text Solution
We have f(x)=x2/3−x4/3
Clearly, the domain of the function is R.
f(x)=x2/3(1−x2/3)=x2/3(1−x1/3)(1+x1/3)
Sign of scheme of y=f(x) is as follows:

f′(x)=23x−13−43x13
=231−2x2/3x1/3
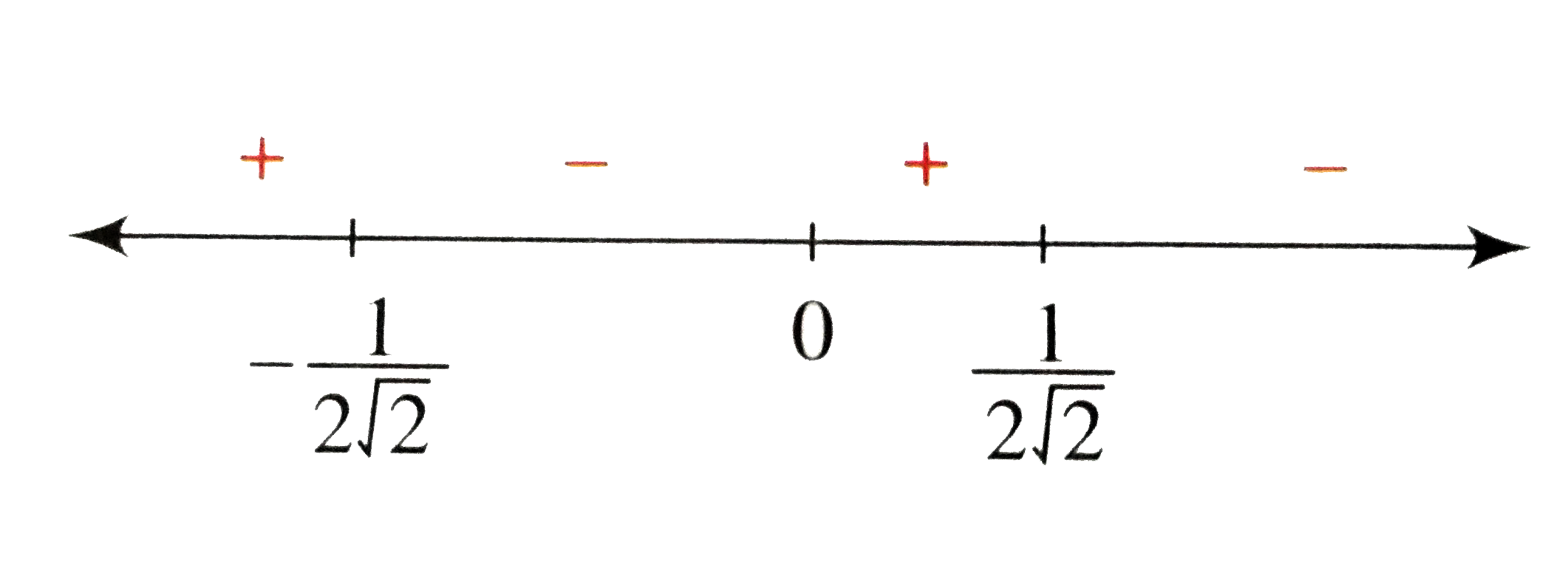
=−43(x1/3−1√2)x13+1√2x13
f′(x)=0∴x=±12√2
Also, f′(x) does not exist at x=0
it is also a critical point.
Sign scheme of f′(x) is as follows:

Thus, x=0 is the point of minima and x=±12√2 are the points of maxima.
f(0)=0,f(x)=0∴x=0,±1
f(±1)=0
Also when, x→±∞,f(x)→−∞
y=f(x) is an even function, so the graph is symmetrical about the y-axis.
At x=0, the graph has vertical tangent line x=0, where the function is non-differentiable.
From the above discussion, the graph of the function is as shown in the following figure.

|
Topper's Solved these Questions
Similar Questions
Draw and discuss the graph of f(x)=x+√x−1
View SolutionDraw the graph of f(x)=12x43−6x13
View SolutionDraw and discuss the graph of the function f(x)=e1/x
View SolutionDraw the graph of f(x)=sgn(x3−x).
View SolutionDraw the graph of f(x)=x|x|.
View SolutionDraw the graph of f(x)=x3−xx2−1.
View SolutionDiscuss the extremum of f(x)=2x+3x23
View SolutionDiscuss the extremum of f(x)=2x+3x23
View SolutionDraw the graph of f(x)=esinx.
View SolutionDraw the graph of f(x)=√1−e−x2
View Solution
