In parallelogram ABCD, ∠A=3cm times ∠B. Find all the angles of the parallelogram. In the same parallelogram, if AB=5x-7 and CD=3x+1, find the length of CD.
The correct Answer is:135∘,45∘,135∘and45∘, CD=13 units.
To solve the problem step by step, we will follow the given information about the parallelogram ABCD, where angle A is three times angle B. We will also find the length of side CD based on the expressions provided.
Step 1: Set up the equations for angles
Given that angle A is three times angle B, we can express this relationship mathematically:
- Let angle B = x
- Then angle A = 3x
Step 2: Use the properties of a parallelogram
In a parallelogram, opposite angles are equal, and the sum of all angles is 360 degrees. Therefore:
- Angle C = angle A = 3x
- Angle D = angle B = x
The equation for the sum of the angles in the parallelogram is:
Angle A+Angle B+Angle C+Angle D=360∘
Substituting the values we have:
3x+x+3x+x=360∘
Step 3: Simplify the equation
Combine like terms:
8x=360∘
Step 4: Solve for x
To find the value of x, divide both sides by 8:
x=360∘8=45∘
Step 5: Find angles A, B, C, and D
Now that we have x, we can find the angles:
- Angle B = x = 45°
- Angle A = 3x = 3(45°) = 135°
- Angle C = angle A = 135°
- Angle D = angle B = 45°
Thus, the angles of the parallelogram are:
- Angle A = 135°
- Angle B = 45°
- Angle C = 135°
- Angle D = 45°
Step 6: Set up the equation for the sides
We are given:
- AB = 5x - 7
- CD = 3x + 1
Since AB = CD in a parallelogram, we can set up the equation:
5x−7=3x+1
Step 7: Solve for x
Rearranging the equation gives:
5x−3x=1+7
2x=8
x=4
Step 8: Find the length of CD
Now substitute x back into the expression for CD:
CD=3x+1=3(4)+1=12+1=13
Final Answer
The angles of the parallelogram ABCD are:
- Angle A = 135°
- Angle B = 45°
- Angle C = 135°
- Angle D = 45°
The length of CD is:
- CD = 13 units
Given that angle A is three times angle B, we can express this relationship mathematically:
- Let angle B = x
- Then angle A = 3x
In a parallelogram, opposite angles are equal, and the sum of all angles is 360 degrees. Therefore:
- Angle C = angle A = 3x
- Angle D = angle B = x
Angle A+Angle B+Angle C+Angle D=360∘
Substituting the values we have:
3x+x+3x+x=360∘
Combine like terms:
8x=360∘
To find the value of x, divide both sides by 8:
x=360∘8=45∘
Now that we have x, we can find the angles:
- Angle B = x = 45°
- Angle A = 3x = 3(45°) = 135°
- Angle C = angle A = 135°
- Angle D = angle B = 45°
- Angle A = 135°
- Angle B = 45°
- Angle C = 135°
- Angle D = 45°
We are given:
- AB = 5x - 7
- CD = 3x + 1
5x−7=3x+1
Rearranging the equation gives:
5x−3x=1+7
2x=8
x=4
Now substitute x back into the expression for CD:
CD=3x+1=3(4)+1=12+1=13
The angles of the parallelogram ABCD are:
- Angle A = 135°
- Angle B = 45°
- Angle C = 135°
- Angle D = 45°
- CD = 13 units
Topper's Solved these Questions
Similar Questions
Knowledge Check

In parallelogram ABCD above, AC=3 and AD=5. What is the area of ABCD?A12B15C18D20
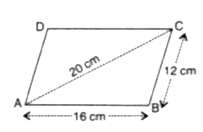
In parallelogram ABCD, AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram.
View SolutionFind the angles of the parallelogram ABCD, if
∠C=23∠D
View SolutionIf the adjacent angles of a parallelogram are in the ratio 13:12. Find all the angles of parallelogram.
View SolutionIn the given figure, AB∣∣CD,AB=7cm,BD=25cmandCD=17cm, find the length of side BC.

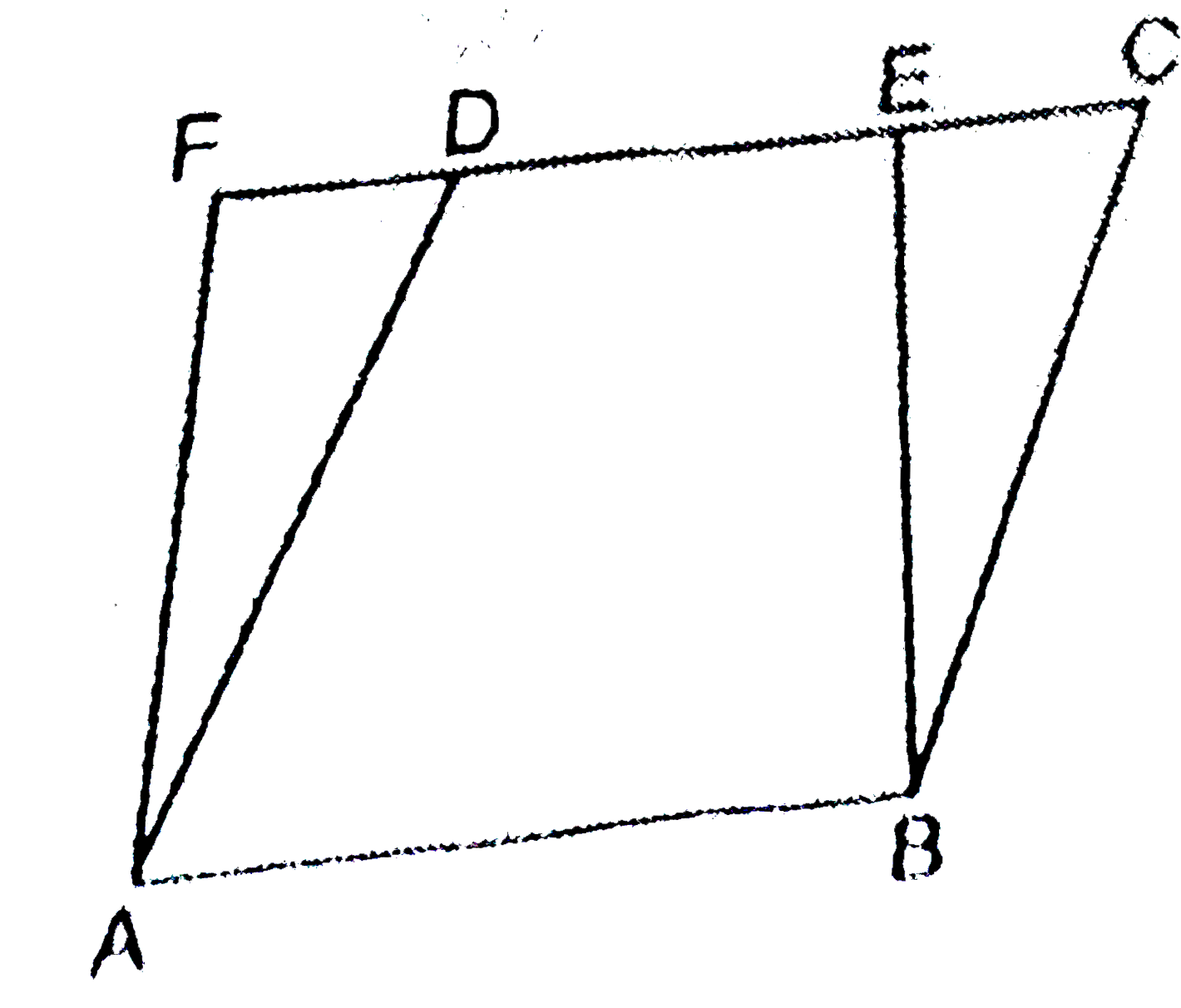
View SolutionIn the given figure, if the area of parallelogram ABCD is 40cm2, find the area of parallelogram ABEF
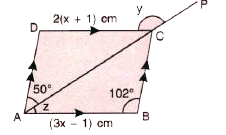
View SolutionIn the given figure, ABCD is a parallelogram. Find the values of x, y and z
View SolutionThree vertices of a parallelogram ABCD taken in order are A (3, 6), B (5, 10) and C (3, 2) find :
(ii) length of diagonal BD.
View Solution
