In parallelogram ABCD, points P and Q lie on side BC and trisect it. Prove that :
ar.(ΔAPQ)=ar.(ΔDPQ)
=16×ar. (Parallelogram ABCD)
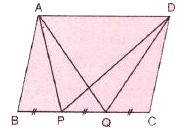
Step by step video & image solution for In parallelogram ABCD, points P and Q lie on side BC and trisect it. Prove that : ar.(DeltaAPQ)=ar.(DeltaDPQ) =(1)/(6)xxar. (Parallelogram ABCD) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(A)
36 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(B)
16 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
Similar Questions
Given a parallelogram ABCD where X and Y are the mid-points of the sides BC and CD respectively . Prove that:
ar (ΔAXY)=38×ar(/gm)ABCD
View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= 18 of the area of parallelogram ABCD.
View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= 18 of the area of parallelogram ABCD.
View SolutionIn parallelogram ABCD, P is a point on side AB and Q is a ponit on side BC.
Prove that :
(i) ΔCPD and ΔAQD are equal in area.
(ii) Area (ΔAQD)
=Area(ΔAPD)+Area(ΔCPB)
View SolutionIn parallelogram ABCD, P is a point on side AB and Q is a ponit on side BC.
Prove that :
(i) ΔCPD and ΔAQD are equal in area.
(ii) Area (ΔAQD)
=Area(ΔAPD)+Area(ΔCPB)
View SolutionThe diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
View SolutionABCD is a parallelogram. Two points P and Q are taken on sides AD and BC respectively such that AP 13ADandCQ=13BC. Prove that □AQCP is a parallelogram.
View SolutionIn parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that

BC= BE
View SolutionIn a parallelogram ABCD, X and Y are points on diagonal BD such that DX=BY. Prove that AXCY is a parallelogram.
View Solution
