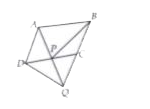
In parallelogram ABCD two points P and Q are taken on diagonal BD such that DP = BQ (set figure). Show that:
(i)ΔAPD≅CQB(ii)AP=CQ(iii)ΔAQB≅ΔCPD(iv)AQ=CP(v)APCQis a parallelogram. ltbegt 
Step by step video & image solution for In parallelogram ABCD two points P and Q are taken on diagonal BD such that DP = BQ (set figure). Show that: {:((i)DeltaAPD~=CQB,(ii)AP=CQ),((iii)DeltaAQB~=DeltaCPD,(iv)AQ=CP),((v)APCQ "is a parallelogram.",):} ltbegt by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - NCERT SECTION (Exercise 8.2 )
11 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Multiple Choice Questions) (LEVEL-1 )
35 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - SOLVED EXAMPLES
12 Videos
- PROBABILITYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ. Show that:
(i) ΔAPD≅ΔCQB
(ii) AP=CQ
(iii) ΔABC
(iv) AQ=CP
(v) APCQ is a parallelogram.
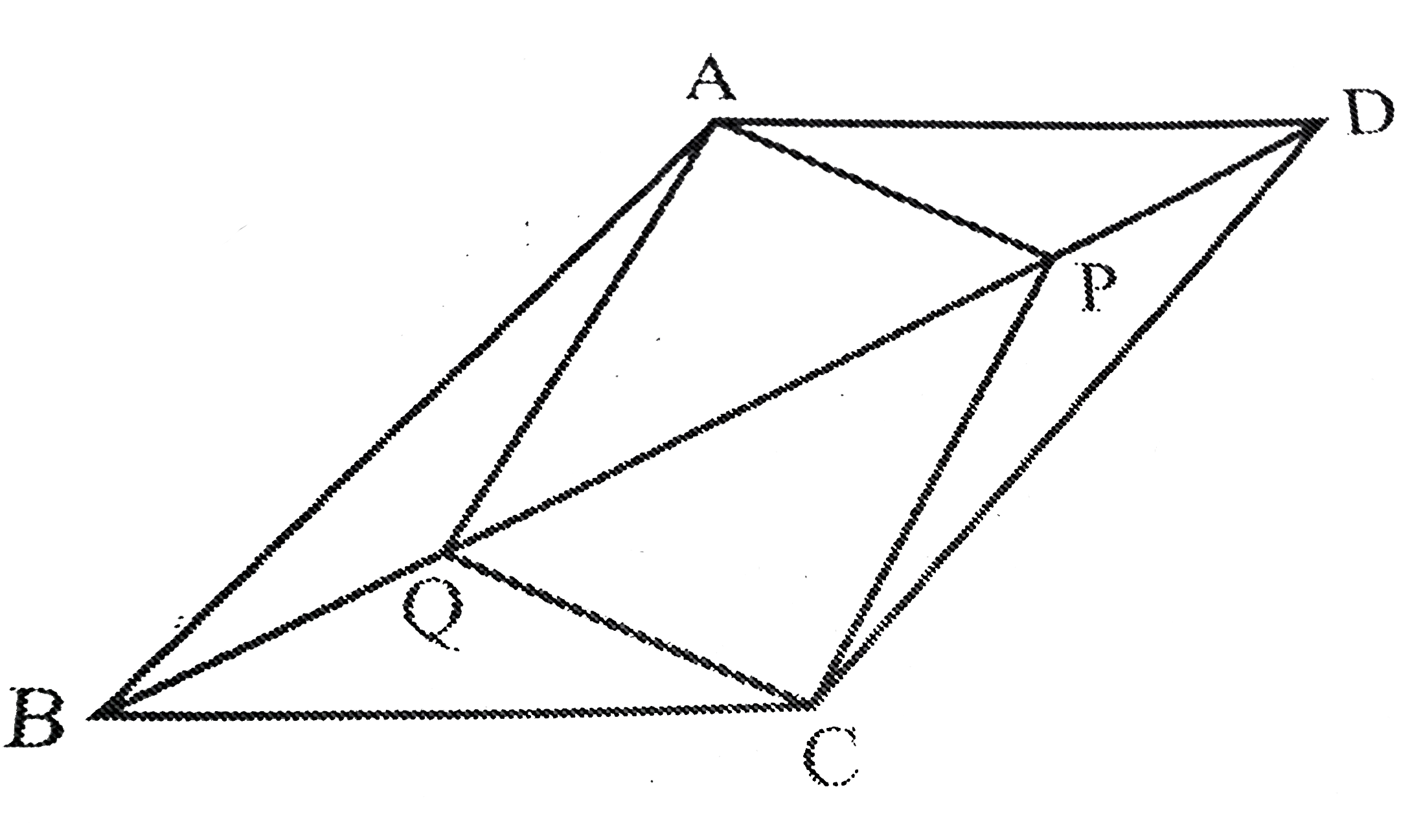
View SolutionIn a parallelogram ABCD, points P and Q are points of trisection of diagonal BD. Prove that CQ is parallel to AP.
View SolutionABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD . Show that
(i) ΔAPB≅ ΔCQD
(ii) AP = CQ
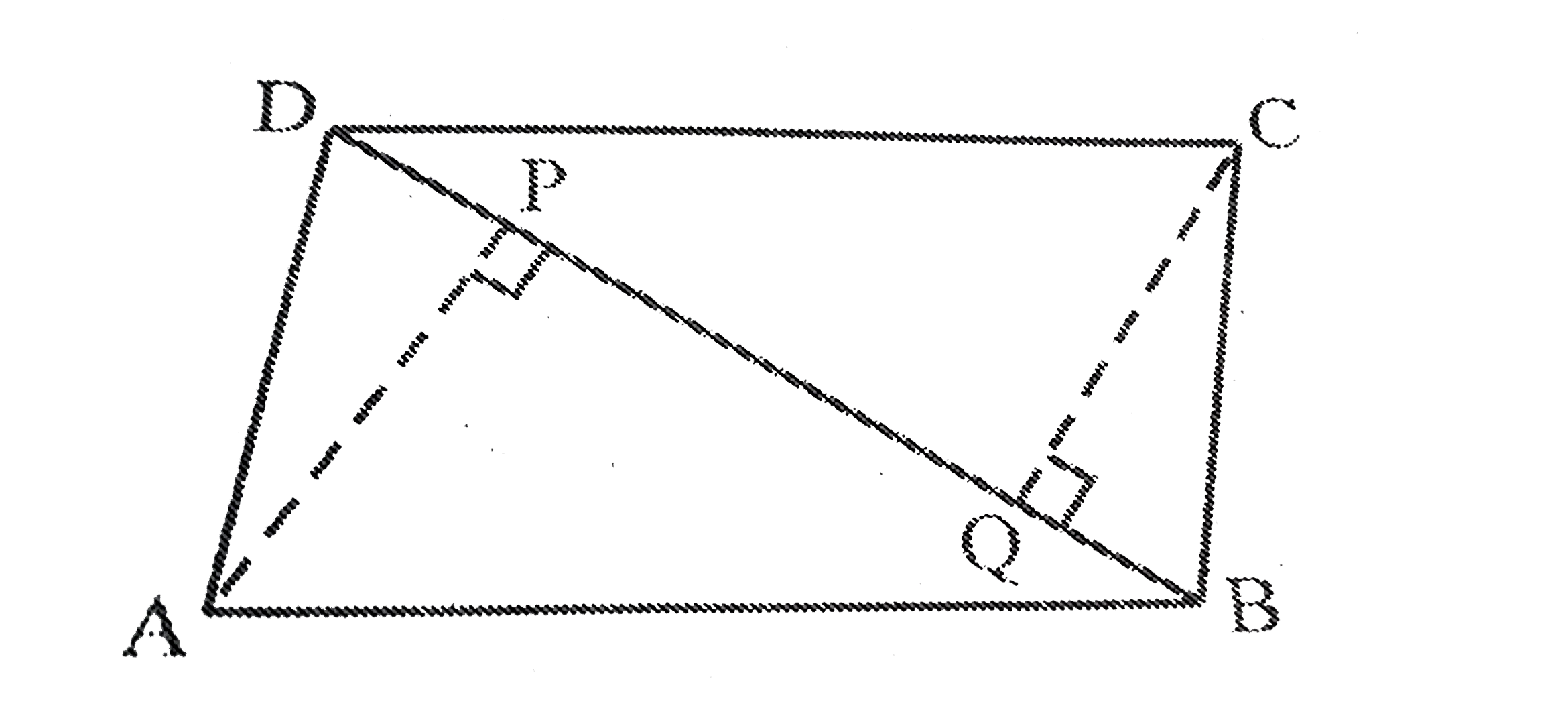
View SolutionIn the given figure, ABCD is a parallelogram in which AN and CP are perpendiculars on diagonal BD. Prove that :
(i) ΔADN=ΔCBP
(ii)AN=CP
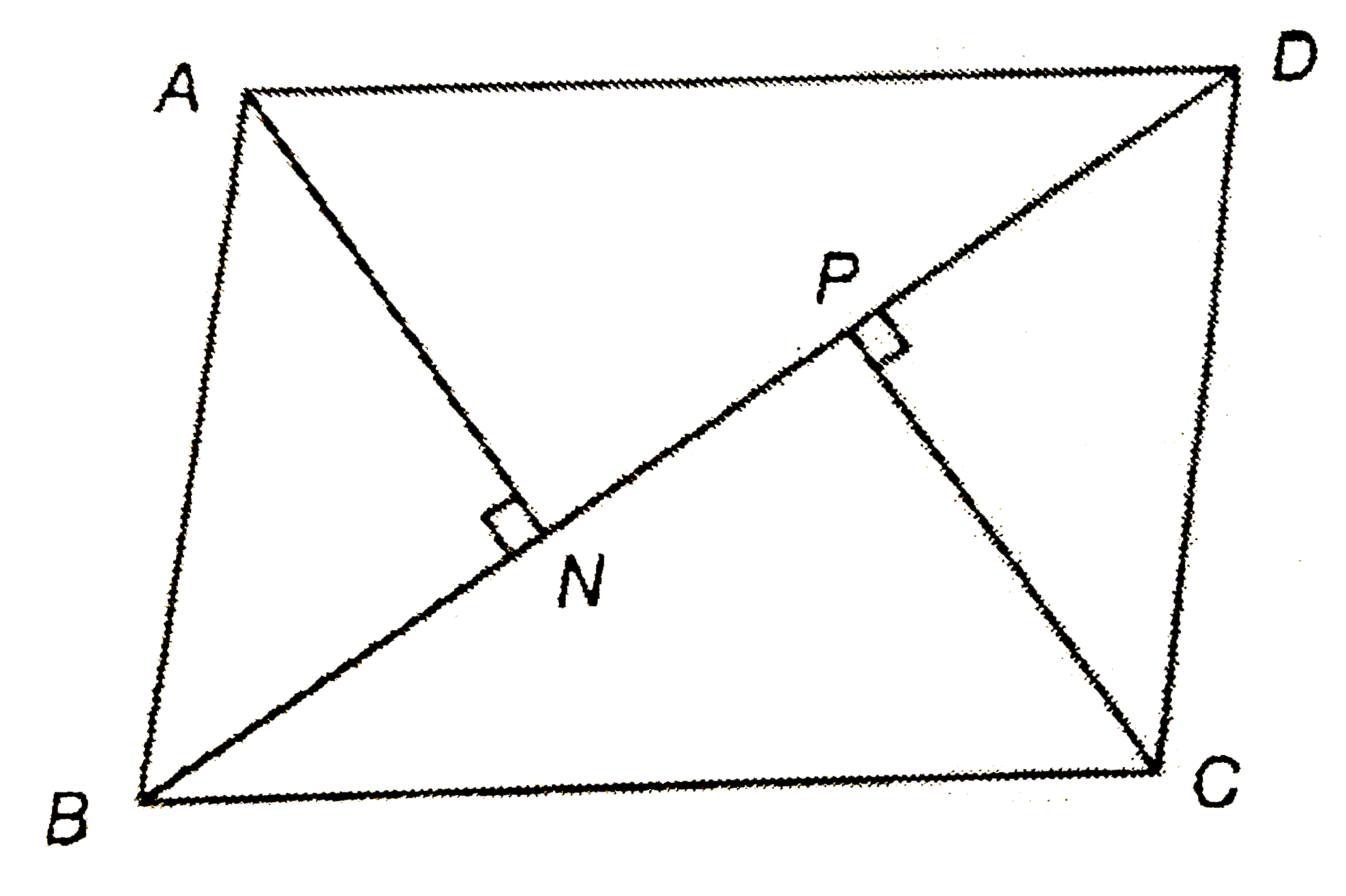
View SolutionIn the figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar(ΔBPC) = ar(ΔDPQ).
View SolutionABCD is a parallelogram. Tow points P and Q are taken on sides AD and BC respectively such that AP 13ADandCQ=13BC. Prove that □AQCP is a parallelogram.
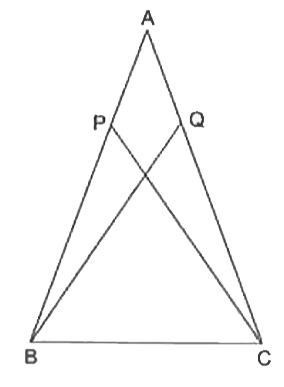
View SolutionIn the adjoining figure, P and Q are two points on equal sides AB and AC of an isosceles triangle ABC such that AP = AQ. Prove that BQ = CP.
View SolutionABCD is a parallelogram in which P and Q are midpoints of opposite sides AB and CD respectively (see figure). If AQ intersects DP at S and BQ intersects CP at R, show that:
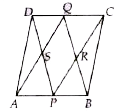
(i) APCQ is a parallelogram.
View SolutionABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and CD (see Fig. 8.18). If AQ intersects DP at S and BQ intersects CP at R, show that: (i) APCQ is a parallelogram.(ii) DPBQ is a parallelogram.(iii) PSQR is a parallelogram
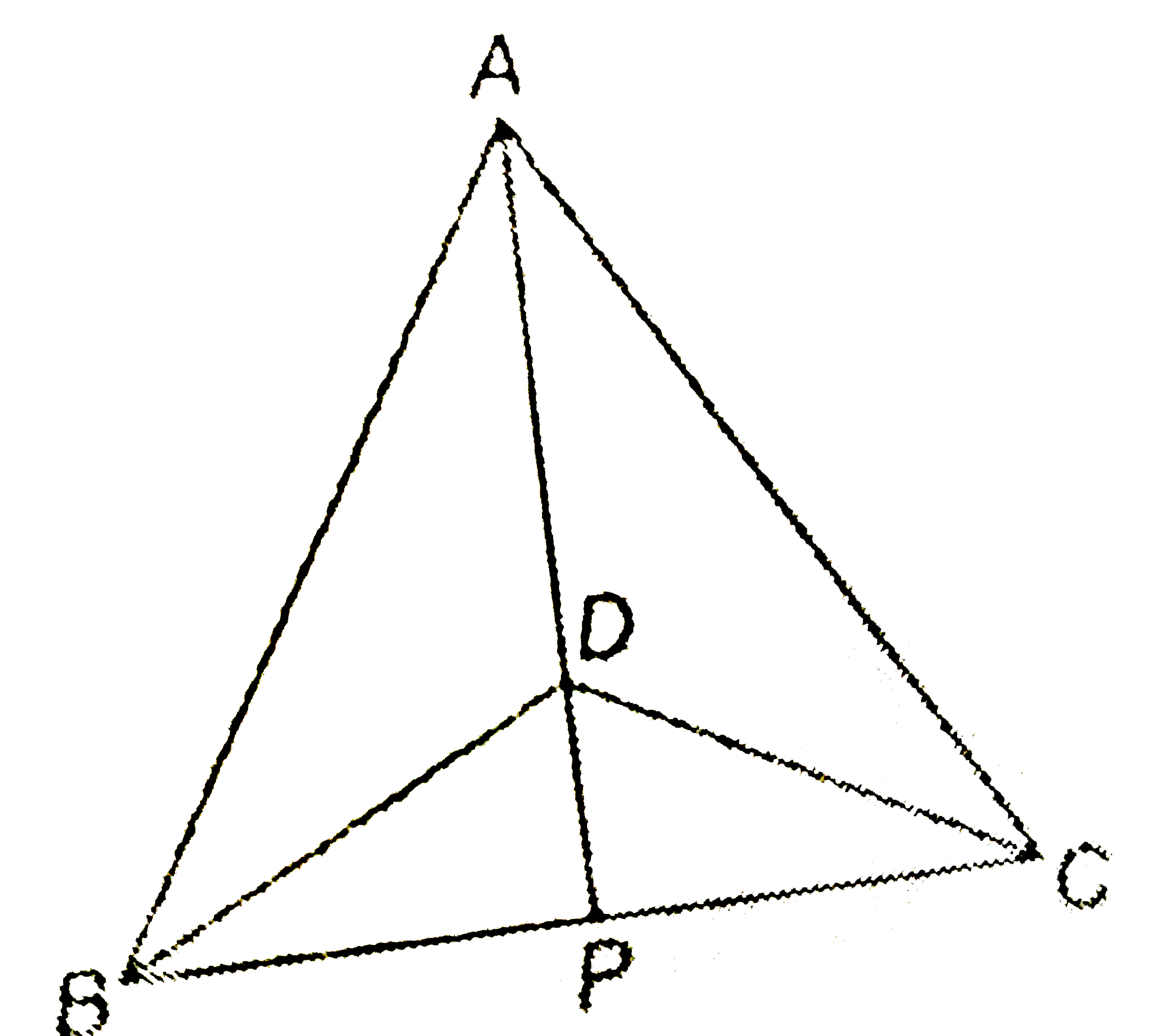
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that :
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
View Solution
