In parallelogram ABCD, X and Y are mid-points of opposite sides AB and DC respectively. Prove that:
(i) AX=YC.
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
To solve the problem, we will follow the steps outlined in the video transcript to prove each part of the question regarding the parallelogram ABCD with midpoints X and Y on sides AB and CD, respectively.
1. Identify the Given Information:
- We have a parallelogram ABCD.
- X is the midpoint of side AB.
- Y is the midpoint of side CD.
2. Prove that AX = YC:
- Since X is the midpoint of AB, we can say:
AX=12AB
- Similarly, since Y is the midpoint of CD, we can say:
YC=12CD
- In a parallelogram, opposite sides are equal, so:
AB=CD
- Therefore, we can conclude:
AX=12AB=12CD=YC
- Hence, we have proved that:
AX=YC
3. Prove that AX is parallel to YC:
- In a parallelogram, opposite sides are parallel. Since AB is parallel to CD, we can say:
AB∥CD
- Since X and Y are midpoints, the segments AX and YC are half of the lengths of AB and CD respectively. Thus:
AX∥YC
- Hence, we have proved that:
AX∥YC
4. Prove that AXCY is a Parallelogram:
- We have already established that AX is equal to YC and that AX is parallel to YC.
- According to the properties of a parallelogram, if one pair of opposite sides is both equal and parallel, then the figure formed is a parallelogram.
- Therefore, since:
AX=YCandAX∥YC
- We conclude that AXCY is a parallelogram.
Final Conclusion:
We have successfully proved all three parts:
1. AX=YC
2. AX∥YC
3. AXCY is a parallelogram.
- We have a parallelogram ABCD.
- X is the midpoint of side AB.
- Y is the midpoint of side CD.
- Since X is the midpoint of AB, we can say:
AX=12AB
- Similarly, since Y is the midpoint of CD, we can say:
YC=12CD
- In a parallelogram, opposite sides are equal, so:
AB=CD
- Therefore, we can conclude:
AX=12AB=12CD=YC
- Hence, we have proved that:
AX=YC
- In a parallelogram, opposite sides are parallel. Since AB is parallel to CD, we can say:
AB∥CD
- Since X and Y are midpoints, the segments AX and YC are half of the lengths of AB and CD respectively. Thus:
AX∥YC
- Hence, we have proved that:
AX∥YC
- We have already established that AX is equal to YC and that AX is parallel to YC.
- According to the properties of a parallelogram, if one pair of opposite sides is both equal and parallel, then the figure formed is a parallelogram.
- Therefore, since:
AX=YCandAX∥YC
- We conclude that AXCY is a parallelogram.
We have successfully proved all three parts:
1. AX=YC
2. AX∥YC
3. AXCY is a parallelogram.
Topper's Solved these Questions
Similar Questions
Given a parallelogram ABCD where X and Y are the mid-points of the sides BC and CD respectively . Prove that:
ar (ΔAXY)=38×ar(/gm)ABCD
View SolutionIn a parallelogram ABCD, AX and CY are the bisectors of ∠Aand∠C respectively. Prove that AX||CY.
View SolutionIn triangle ABC, D and E are mid-points of sides AB and BC respectively. Also, F is a point in side AC so that DF is parallel to BC
(i) Prove that DBEF is a parallelogram.
View SolutionIn parallelogram ABCD, E is the mid-point of side AB and CE bisect angle BCD. Prove that :
(i) AE=AD
(ii) DE bisect ∠ADC and
(iii) Angle DEC is a right angle.
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid-points of sides AB and DC respectively. Show that AXCY is a parallelogram.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.
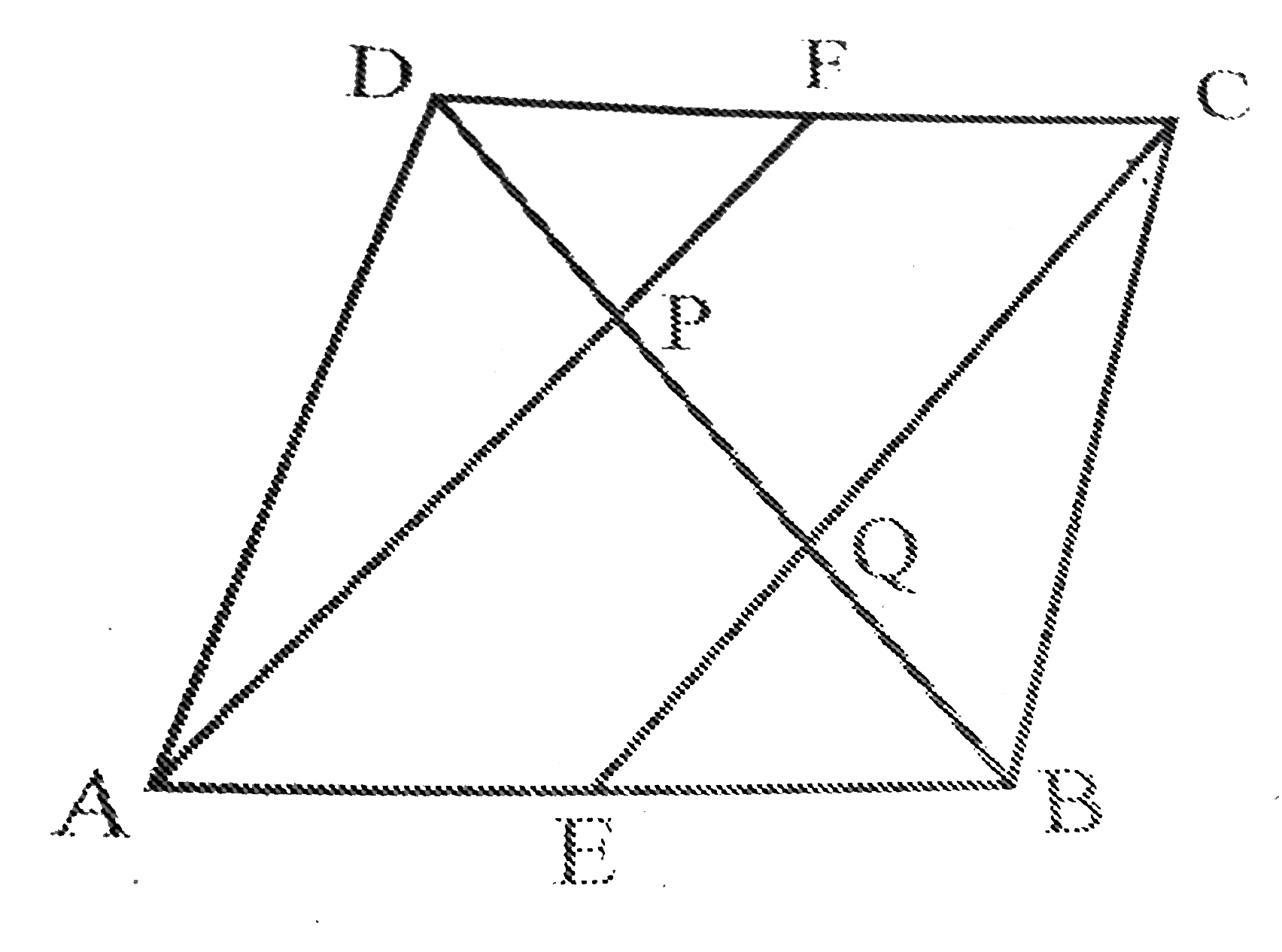
View SolutionX and Y are the mid-points of the opposite sides AB and DC of a parallelogram ABCD. Prove that □AXCY is a parallelogram.
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram. Figure
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides BC and AD respectively. Show that the line segment BF and ED trisect the diagonal AC.
View Solution
