In , if and , then is equal to
To solve the problem, we need to find the measure of angle R in triangle PQR, given that PQ = QR and ∠Q = 100°.
1. Identify the properties of the triangle:
Since PQ = QR, triangle PQR is an isosceles triangle. In an isosceles triangle, the angles opposite the equal sides are equal.
Hint: Remember that in an isosceles triangle, the angles opposite the equal sides are equal.
2. Set up the equation for angles:
Let angle R = angle P (since PQ = QR). We can denote both angles as x. Therefore, we have:
- ∠P = x
- ∠R = x
Hint: Use a variable to represent the equal angles for easier calculations.
3. Use the angle sum property of triangles:
The sum of the angles in any triangle is 180°. Therefore, we can write the equation:
∠P+∠Q+∠R=180°
Substituting the known values:
x+100°+x=180°
Hint: Always remember the angle sum property when dealing with triangles.
4. Combine like terms:
Combine the x terms:
2x+100°=180°
Hint: Combine similar terms to simplify the equation.
5. Isolate the variable:
Subtract 100° from both sides:
2x=180°−100°
2x=80°
Hint: Isolating the variable helps in finding its value more easily.
6. Solve for x:
Divide both sides by 2:
x=80°2=40°
Hint: When you divide, make sure to perform the operation on both sides of the equation.
7. Conclusion:
Since x represents both ∠P and ∠R, we find that:
∠R=40°
Therefore, the measure of angle R is 40°.
Final Answer:
∠R = 40°
Since PQ = QR, triangle PQR is an isosceles triangle. In an isosceles triangle, the angles opposite the equal sides are equal.
Let angle R = angle P (since PQ = QR). We can denote both angles as x. Therefore, we have:
- ∠P = x
- ∠R = x
The sum of the angles in any triangle is 180°. Therefore, we can write the equation:
∠P+∠Q+∠R=180°
Substituting the known values:
x+100°+x=180°
Combine the x terms:
2x+100°=180°
Subtract 100° from both sides:
2x=180°−100°
2x=80°
Divide both sides by 2:
x=80°2=40°
Since x represents both ∠P and ∠R, we find that:
∠R=40°
∠R = 40°
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT EXEMPLARCHAPTER - TRIANGLESEXERCISE - EXERCISE FILL IN THE BLANKS
2 Videos
- TRIANGLESBOOK - NCERT EXEMPLARCHAPTER - TRIANGLESEXERCISE - EXERCISE TRUE OR FALSE
69 Videos
- TRIANGLESBOOK - NCERT EXEMPLARCHAPTER - TRIANGLESEXERCISE - THINK AND DISCUSS
4 Videos
- SIMPLE EQUATIONSBOOK - NCERT EXEMPLARCHAPTER - SIMPLE EQUATIONSEXERCISE - Thick and Discuss
6 Videos
Similar Questions
In ΔPQR, if ∠P=60°,and∠Q=40°, then the exterior angle formed by producing QR is equal to
View SolutionTriangle PQR is a right-angled at Q. If PQ=6 cm , PR=10 cm, then QR is equal to:
त्रिभुज PQR एक समकोण त्रिभुज है जिसमें Q समकोण है | यदि PQ = 6 सेमी, PR = 10 सेमी है, तो QR किसके बराबर होगा ?
View Solution
Knowledge Check
△PQR and △JWN are similar. If 3PQ = JW and WN = 9 cm, then QR is equal to
A3 cmB6cmC9 cmD12 cmIn the figure given below, ∠PQR=90∘andQL is a median, PQ=5cmandQR=12cm. Then QL is equal to
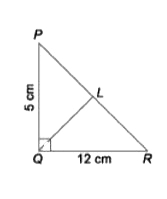 A5 cmB5.5 cmC6 cmD6.5 cm
A5 cmB5.5 cmC6 cmD6.5 cmIn ΔPQR,Q is a right angle, PQ = 3 and QR = 4. If ∠P=αandR=β, then tan β is equal to
A43B34C35D53
In ΔPQR,Q is a right angle, PQ=3andQR=4. If ∠P=αandR=β, then tanβ is equal to
View SolutionIf p:q=3:2 and q:r=6:5 then p:q:r is equal to
View SolutionIn a triangle PQR,PQ=PR and ∠Q is twice that of ∠P. Then ∠Q Is equal to
View SolutionIf P: Q =8.15 and Q:R =3:2 , then find P:Q:R
View SolutionIn triangle PQR, points A,B, and C are taken on PQ, PR and QR respectively such that QC=AC and CR=CB . If ∠QPR=40∘ then ∠ACB is equal to :
View Solution
