In rhombus ABCD:
(i) if ∠A=74∘, find ∠Band∠C.
(ii) if AD=7⋅5cm, find BC and CD.
The correct Answer is:(i) 106∘and74∘
(ii) BC=CD=7.5 cm.
To solve the problem step by step, we will address each part of the question separately.
Part (i): Finding angles B and C
1. Identify the properties of a rhombus: In a rhombus, opposite angles are equal, and the sum of all angles is 360 degrees.
2. Given information: We know that angle A = 74 degrees.
3. Set up the equation for the angles:
- Since angle A = angle C (opposite angles) and angle B = angle D (opposite angles), we can express the sum of the angles as:
angle A+angle B+angle C+angle D=360∘
- This can be rewritten using the known values:
74∘+angle B+74∘+angle B=360∘
4. Combine like terms:
- This simplifies to:
148∘+2×angle B=360∘
5. Isolate angle B:
- Subtract 148 degrees from both sides:
2×angle B=360∘−148∘
2×angle B=212∘
6. Divide by 2 to find angle B:
- Therefore:
angle B=212∘2=106∘
7. Find angle C: Since angle C = angle A, we have:
- angle C=74∘
Summary of Part (i):
- Angle B = 106 degrees
- Angle C = 74 degrees
Part (ii): Finding sides BC and CD
1. Given information: We know that AD = 7.5 cm.
2. Properties of a rhombus: All sides of a rhombus are equal, meaning:
- AB = BC = CD = AD
3. Since AD = 7.5 cm:
- Therefore, BC = 7.5 cm and CD = 7.5 cm.
Summary of Part (ii):
- BC = 7.5 cm
- CD = 7.5 cm
Final Answers:
- (i) Angle B = 106 degrees, Angle C = 74 degrees.
- (ii) BC = 7.5 cm, CD = 7.5 cm.
2. Given information: We know that angle A = 74 degrees.
- Since angle A = angle C (opposite angles) and angle B = angle D (opposite angles), we can express the sum of the angles as:
angle A+angle B+angle C+angle D=360∘
- This can be rewritten using the known values:
74∘+angle B+74∘+angle B=360∘
- This simplifies to:
148∘+2×angle B=360∘
- Subtract 148 degrees from both sides:
2×angle B=360∘−148∘
2×angle B=212∘
- Therefore:
angle B=212∘2=106∘
- angle C=74∘
- Angle B = 106 degrees
- Angle C = 74 degrees
- AB = BC = CD = AD
- Therefore, BC = 7.5 cm and CD = 7.5 cm.
- BC = 7.5 cm
- CD = 7.5 cm
- (i) Angle B = 106 degrees, Angle C = 74 degrees.
- (ii) BC = 7.5 cm, CD = 7.5 cm.
Topper's Solved these Questions
Similar Questions
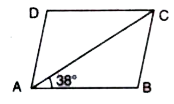
ABCD is a rhombus. If ∠BAC=38∘, find:
(i) ∠ACB
(ii) ∠DAC
(iii) ∠ADC.
View SolutionConstruct a rhombus ABCD, if:
(i) AB=4 cm and ∠B=120∘.
(ii) BC=4.7cmand∠B=75∘.
(iii) CD=5cm and diagonal BD=8.5cm.
View SolutionIn the figure if AB || CD and AD||BC, find ∠Aand∠D
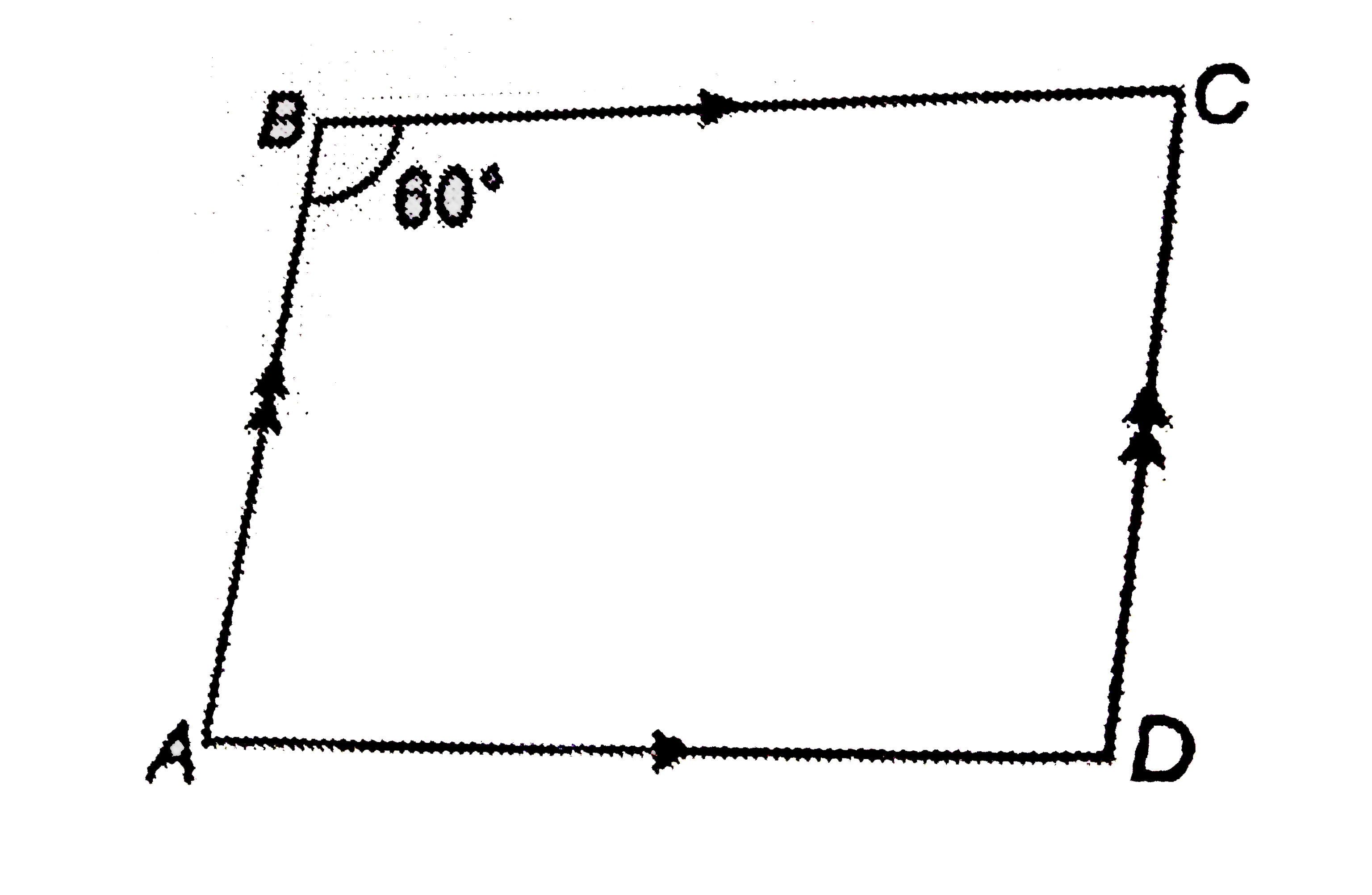
View SolutionIn a ΔABC, if ∠A=45∘.∠B=60∘and∠C=75∘, find the ratio of its sides.
View SolutionIn △ABC,AB=10cm,∠A=45∘ and ∠C=60∘. Find BC.
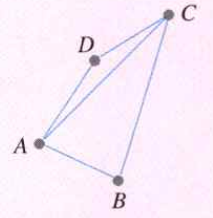
View SolutionFind ∠A+∠B+∠C+∠D
View SolutionIn ΔABC,∠B=90∘,∠A=30∘,b=20cm, find a and c.
View SolutionIn ΔABC,∠A=x+15∘,∠B=xand∠C=2x−35∘ find, each angle of the triangle.
View SolutionIn in △ABC,∠C=105∘,∠B=45∘ and a=2 cm, then find the value of b.
View SolutionIn the adjoining figure, ABCD is a rhombus and ABE is an equilateral triangle. If ∠BCD=70∘, find
(a)∠ADE (b)∠BDE (c)∠BED

View Solution
