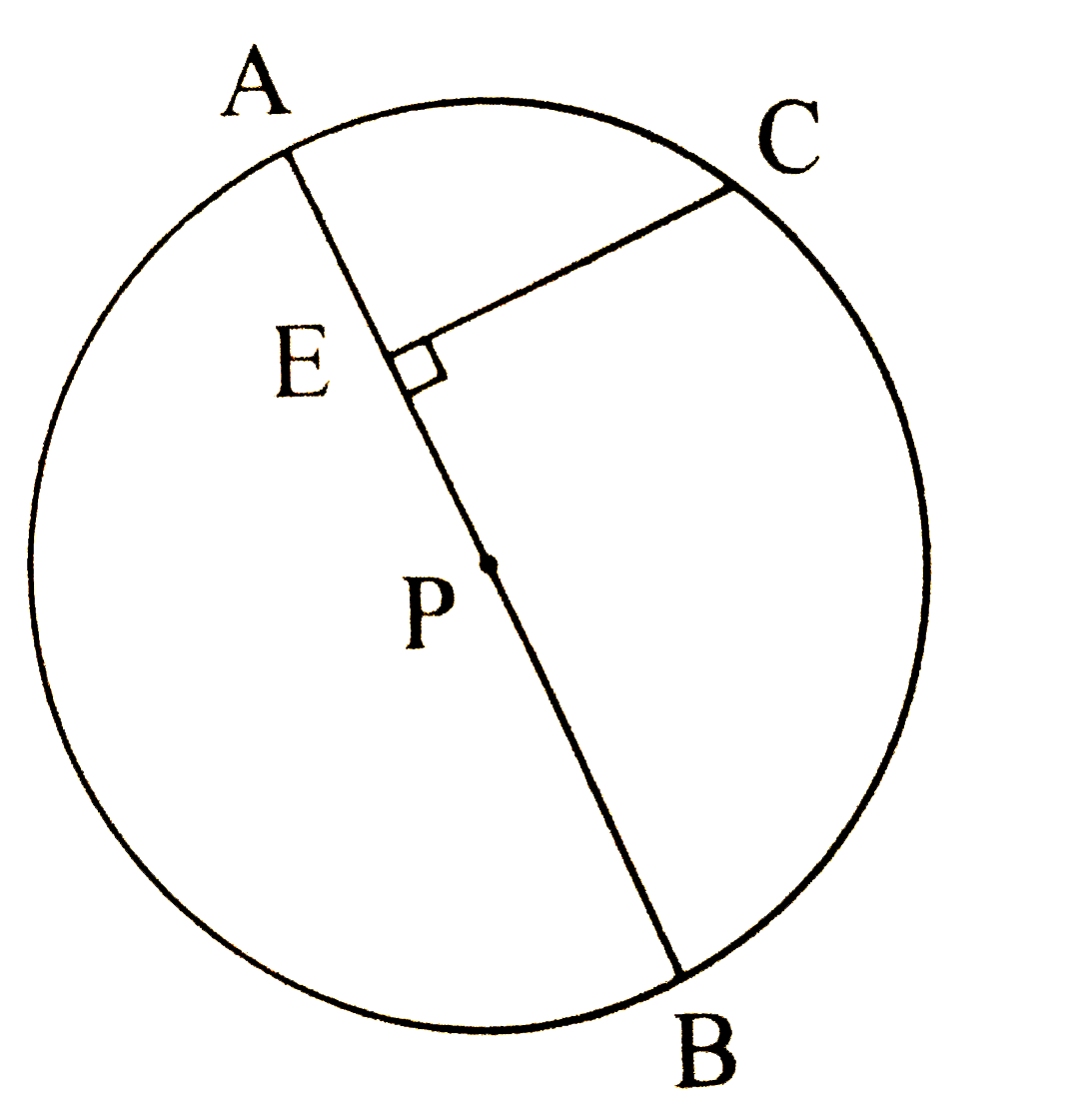
In the above figure, seg AB is a diameter of a circle with centre P.C is any point on the circle. Seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of folloing steps:
(a) Draw ray CE. It intersects the circle at D.
(b) Show that CE = ED.
Write the result using theorem of intersection of chords insides a circle.
(d) Using CE = ED, complete the proof.
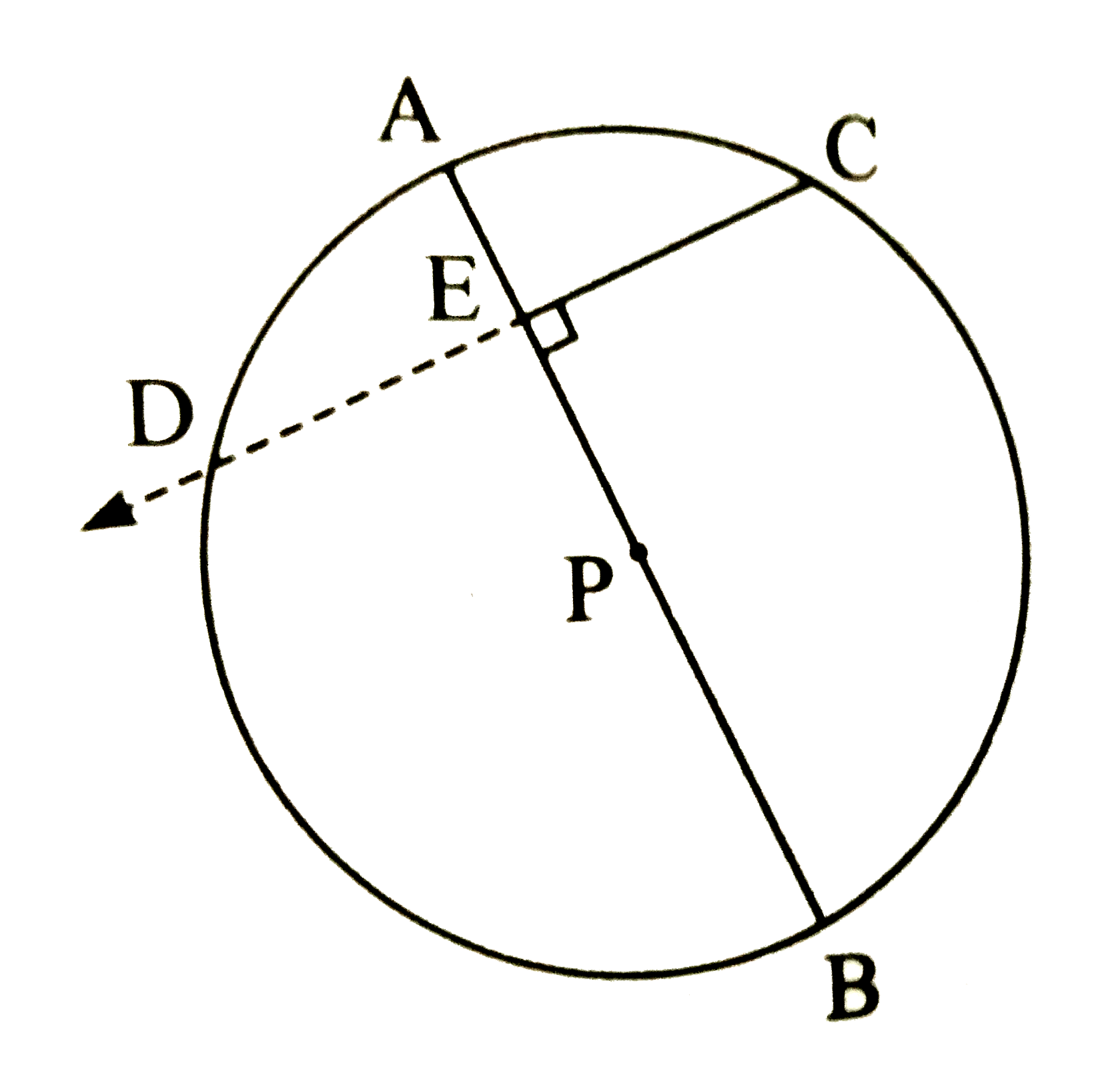
In circle with centre p,AB is a diameter and seg CE ⊥ seg AB ….(Given)
∴ seg PE ⊥ chord CD (Construction)
∴ sec CE ≅ seg DE….(i)
(Perpendicular drawn from centre of the circle to the chord bisects the chord)
seg AB and seg CD are two chords intersecting inside the circle a point E
∴AE×BE=CE×DE
(Theorem of internal division of chords)
AE×BE=CE×CE .... (From i)
AE×BE=CE2
∴CE2=AE×BE
Hence it is proved that CE is the geometric mean of AE and EB.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MODEL QUESTION PAPEREXERCISE - SOLVE ANY TWO THE FOLLOWIN SUBQUESTIONS:3videos
MODEL QUESTION PAPER
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MENSURATIONEXERCISE - Assignment 8.58videos
MENSURATION
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PRACTICE QUESTION BASEDEXERCISE - STATISTICS13videos
PRACTICE QUESTION BASED
Similar Questions
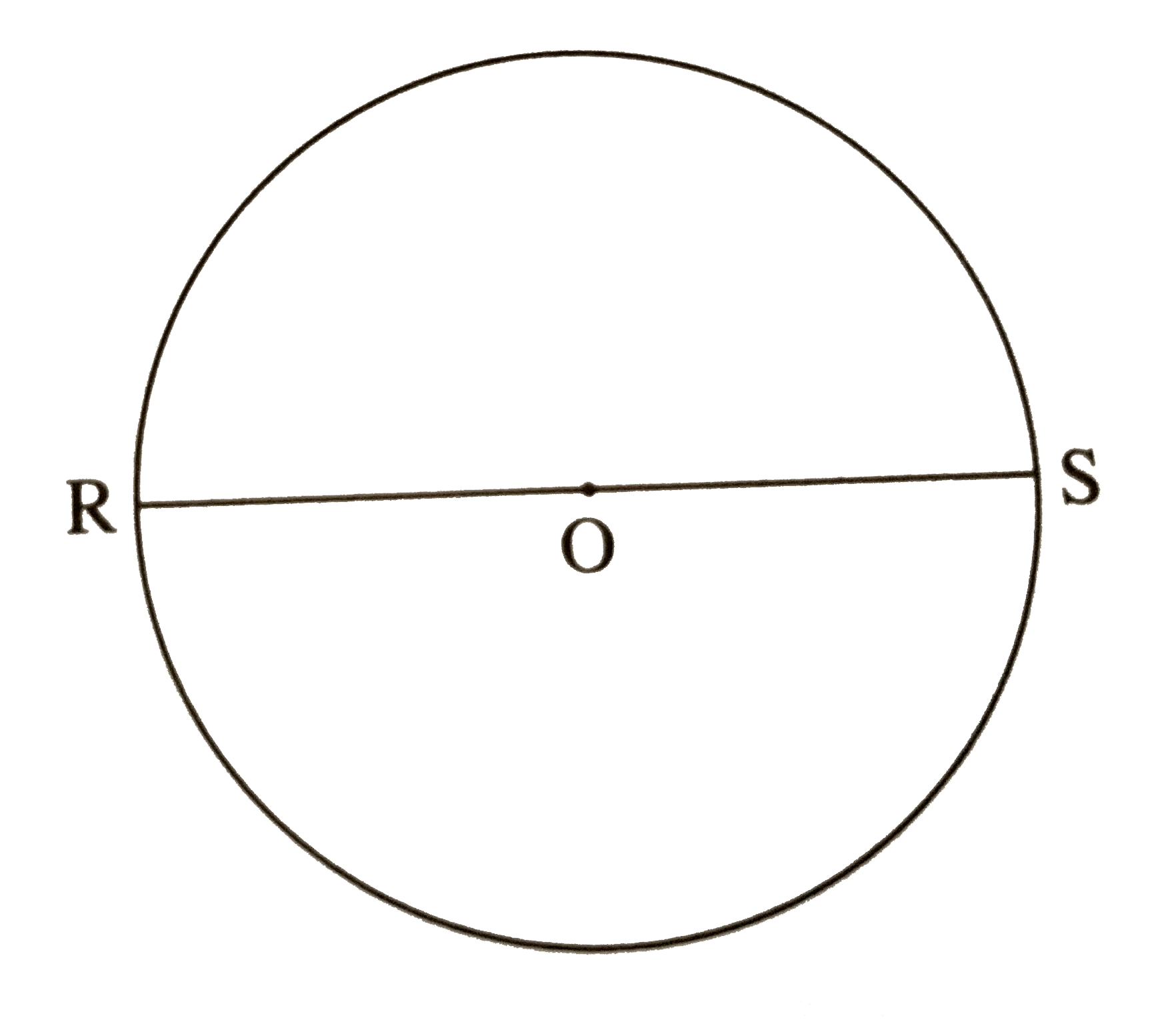
In figure, seg RS is a diameter of the circle with centre O. Point T lines in the exterior of the circle. Prove that ∠RTS is an acute angle.
 View Solution
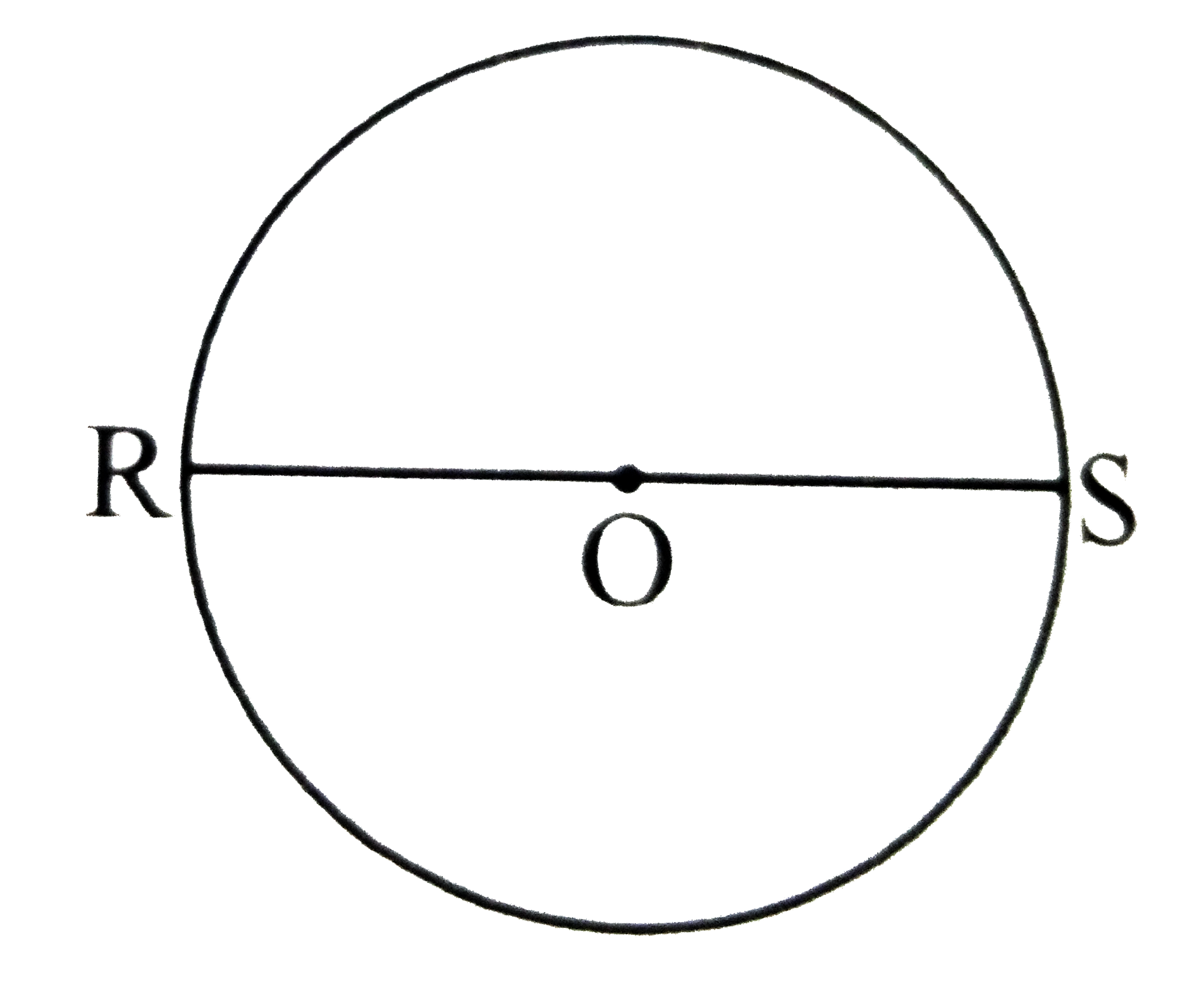
View SolutionIn the adjoining figure, seg RS is a diameter of the circle with centre O. Point T lies in the exterior of the circle. Prove that ∠RTS is an acute angle.
 View Solution
View SolutionIn the adjoining figure, seg AB is a diameter of a circle with centre O. the bisector of ∠ACB intersects the circle at point D. Prove that ,seg AD≅segBD. Complete the following proof by filling the blanks.
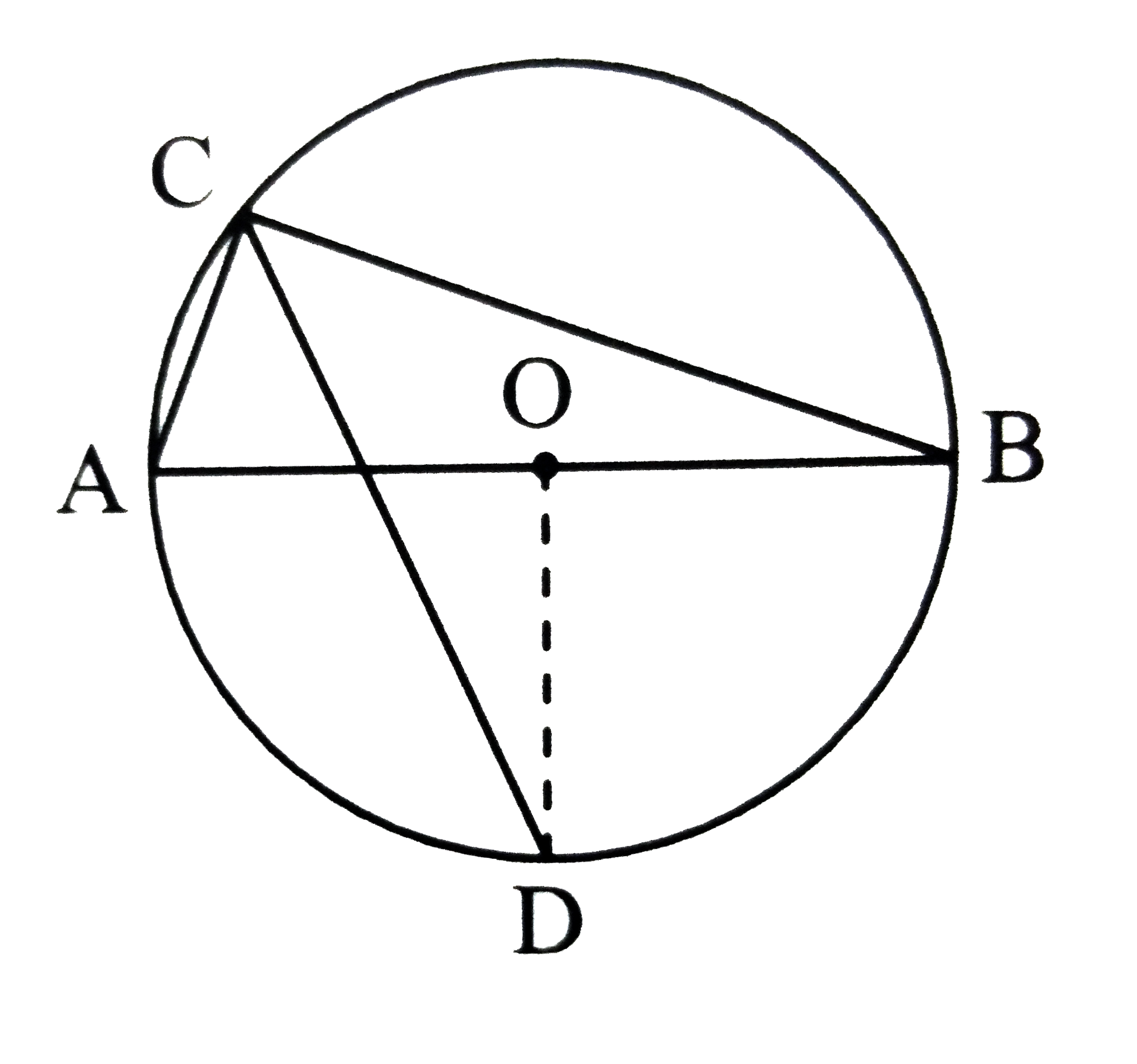 View Solution
View SolutionIn figure, seg AB is a diameter of a circle with centre O. The bisector of ∠ACB intersects the circle at point D. Prove that seg AD ≅ seg BD. Complete the following proof by filling in the blanks
 View Solution
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP⊥ line PQ and seg BQ⊥ line PQ.
Prove that, seg CP≅ seg CQ.
 View Solution
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent, which touches the circle at point T. seg AP ⊥ line PQ and seg BQ ⊥ line PQ. Prove that, seg CP ≅ seg CQ.
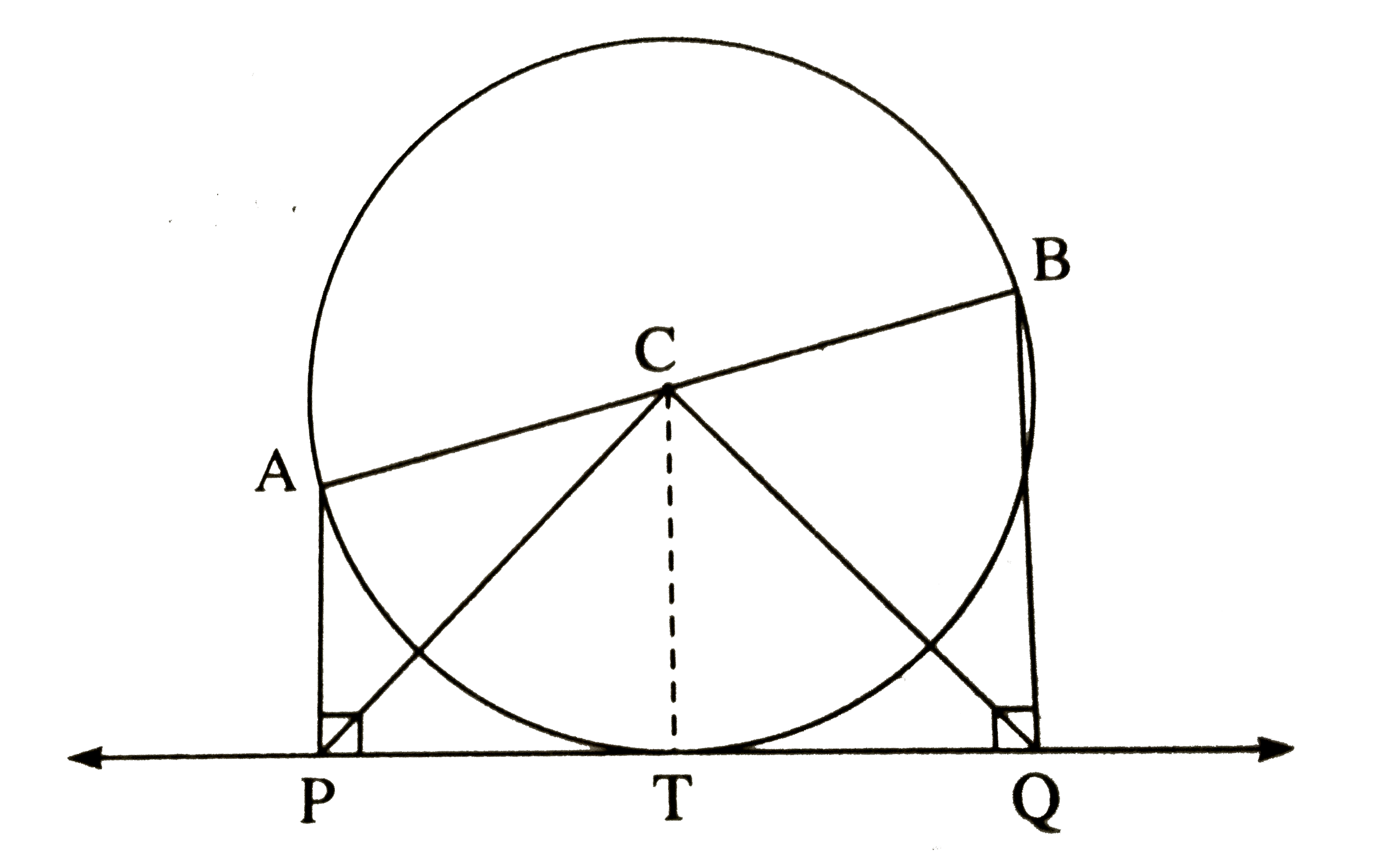 View Solution
View SolutionIn the figure , seg AB is the chord of the circle with centre O. if AM =4 cm then find MB and AB. State your reason.
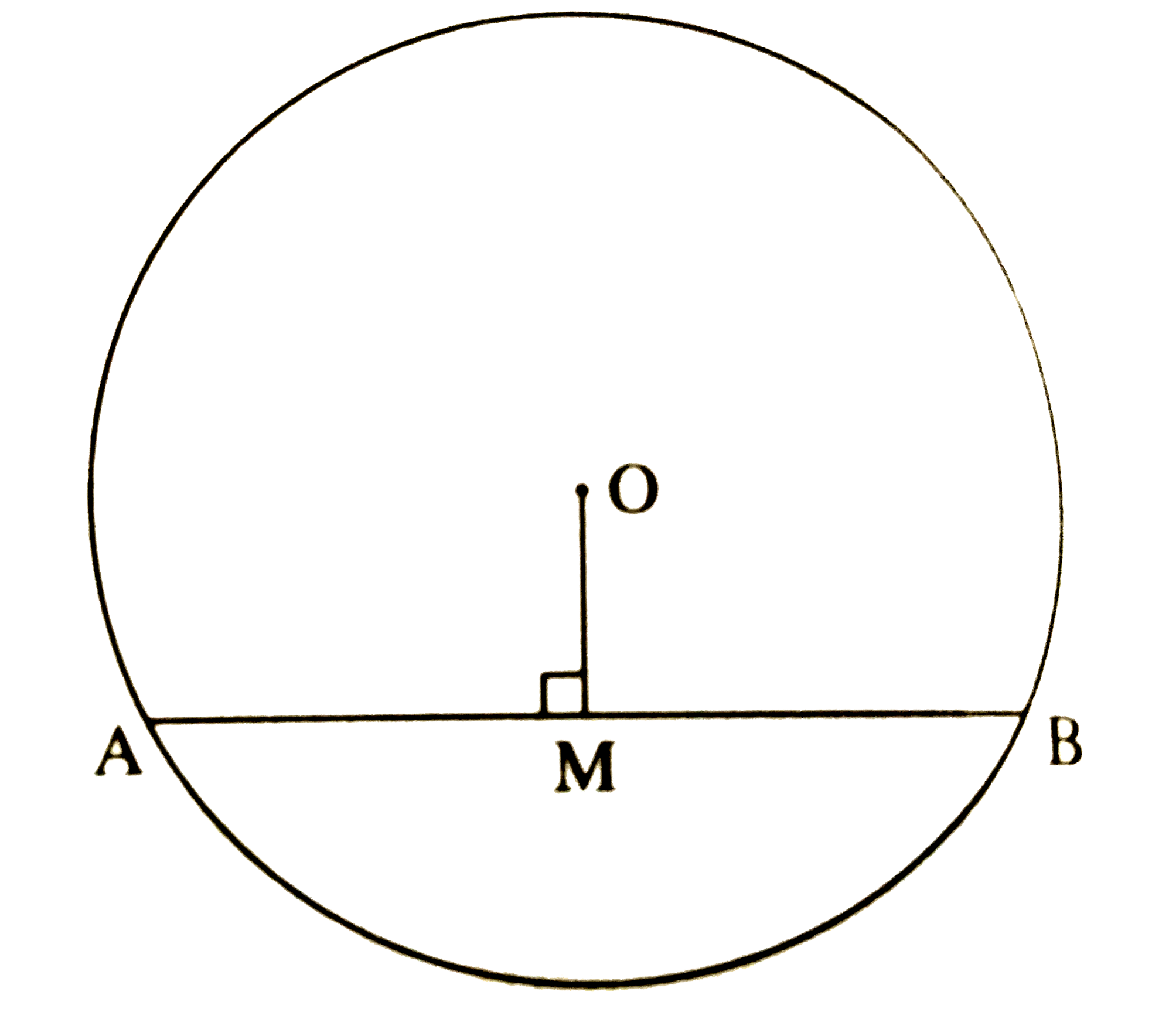 View Solution
View SolutionIn the adjoining figure , seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE×GE=4r2.
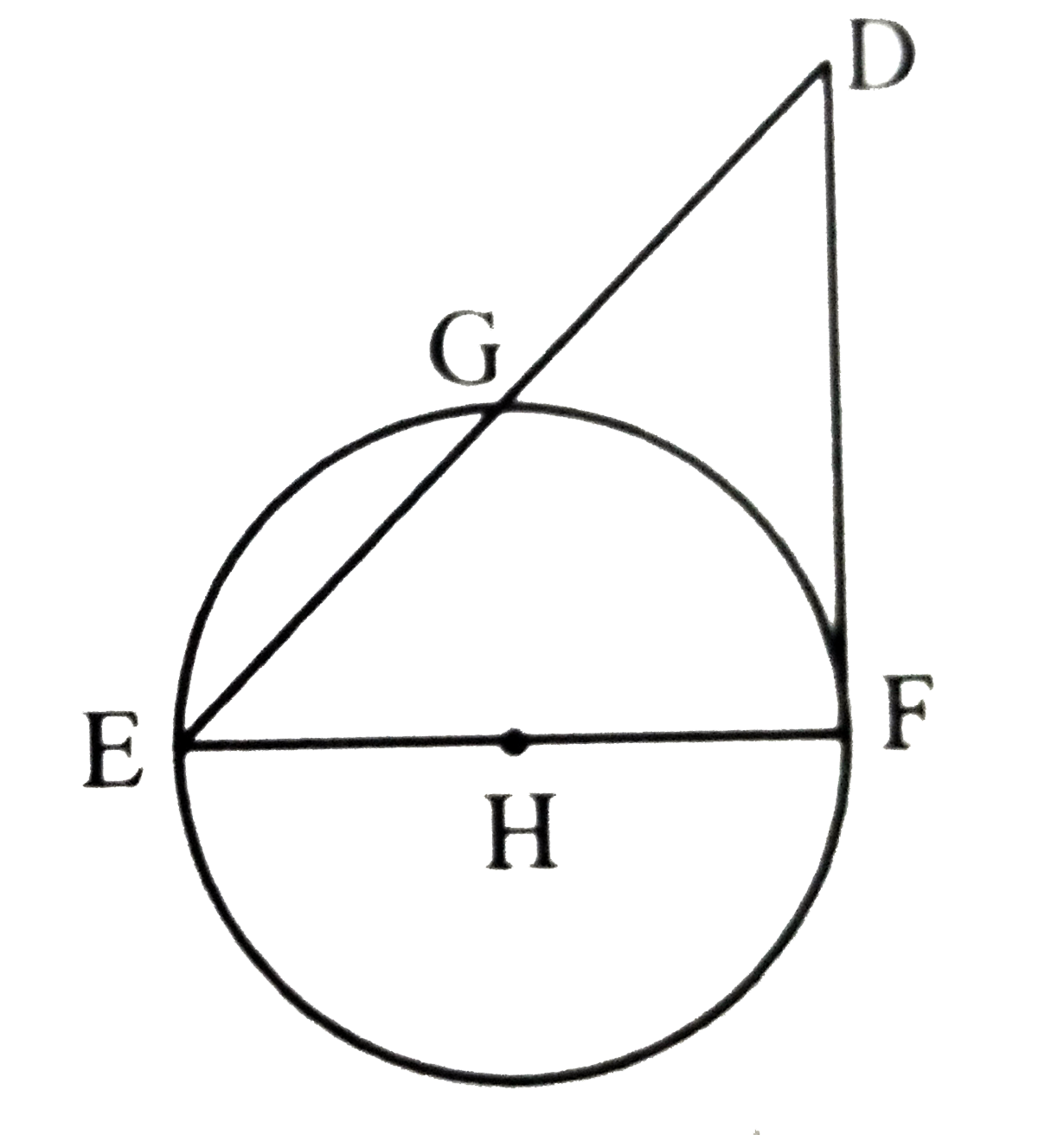 View Solution
View SolutionIn figure, seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE×GE=4r2.
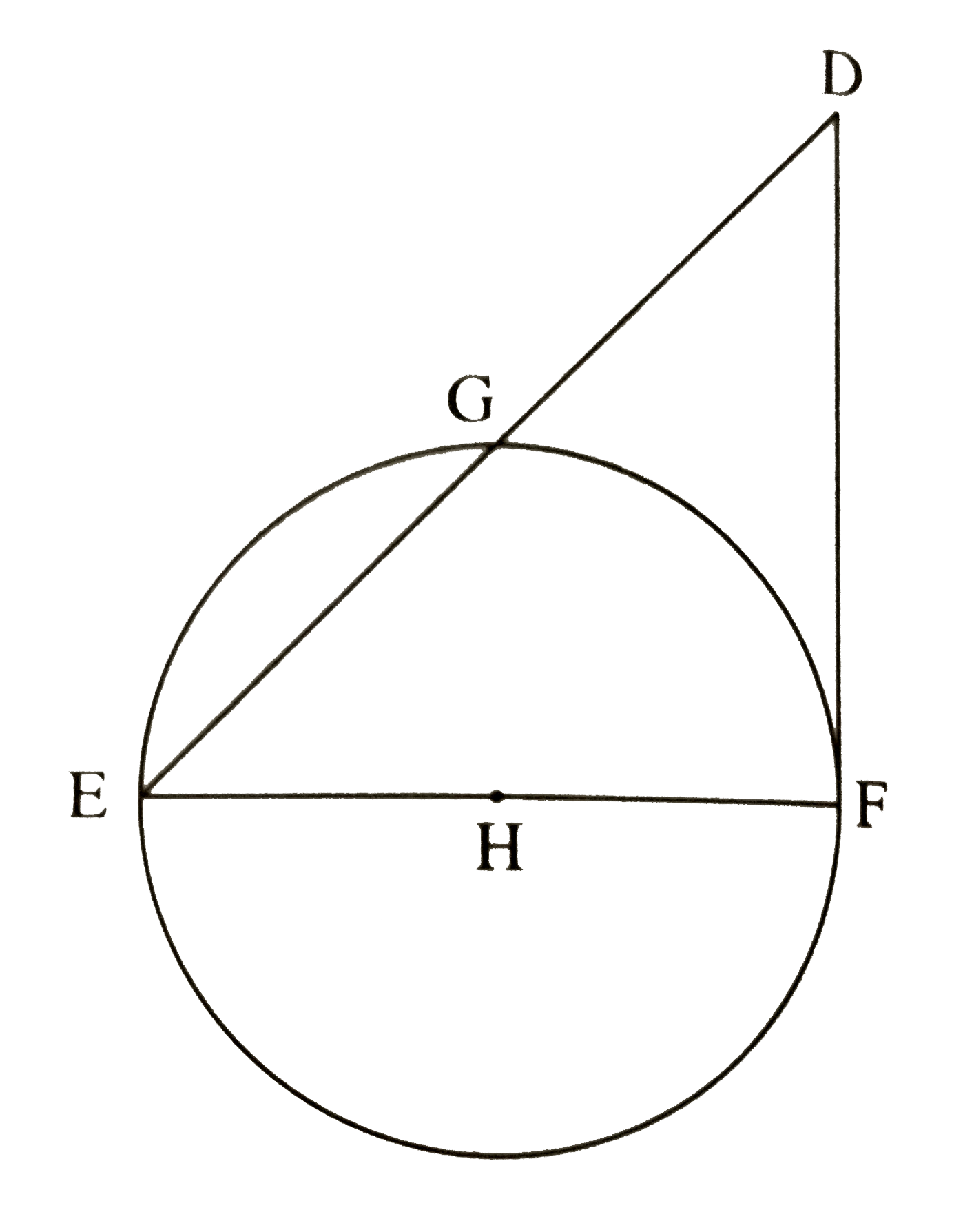 View Solution
View SolutionAB is a chord of a circle with O as centre. C is a point on the circle such that OC is perpendicular to AB and OC intersects AB at P. If PC = 2 cm and AB = 6 cm then the diameter of the circle is
View Solution

