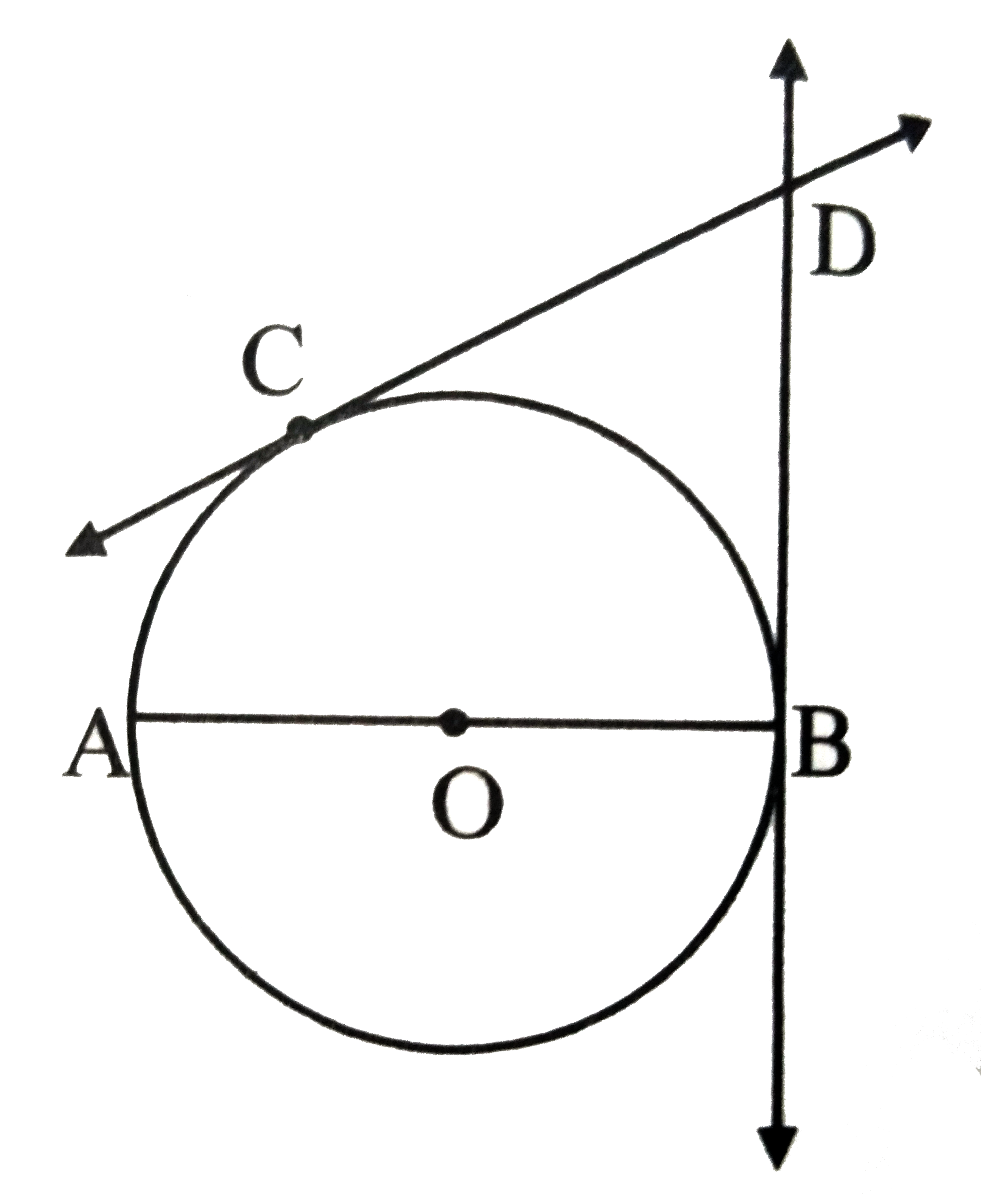
In the adjoining figure , seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE×GE=4r2.
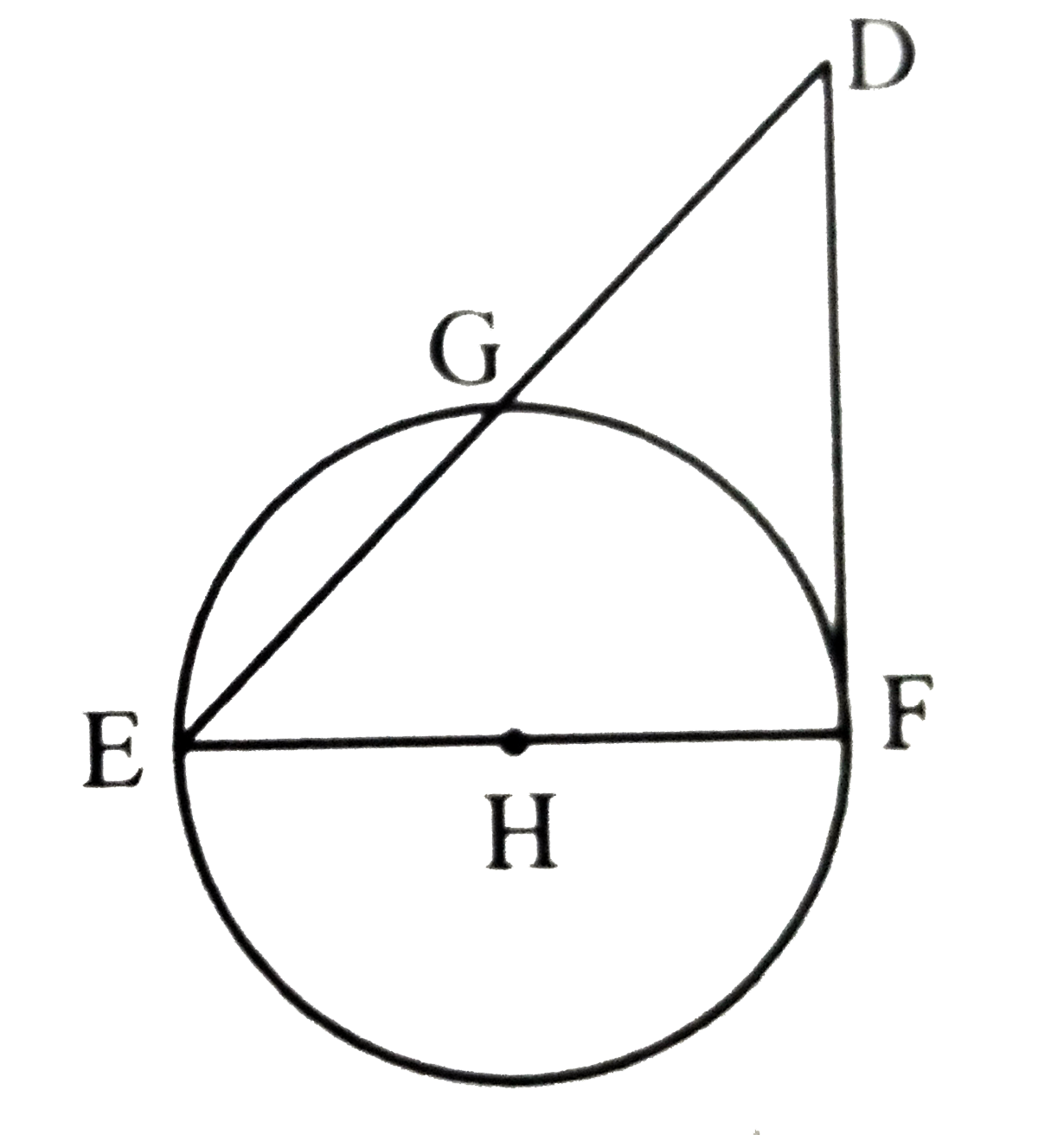
The correct Answer is:∴DE×GE=4r2
Step by step video & image solution for In the adjoining figure , seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DEtimesGE=4r^2. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Problem Set-325videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Activities for Practice4videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Practice Set 3.46videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Chapter 6: Statistics4videos
CHALLENGING QUESTIONS
- BOOK - TARGET PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - CHAPTER ASSESSMENT19videos
CO-ORDINATE GEOMETRY
Similar Questions
In figure, seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE×GE=4r2.
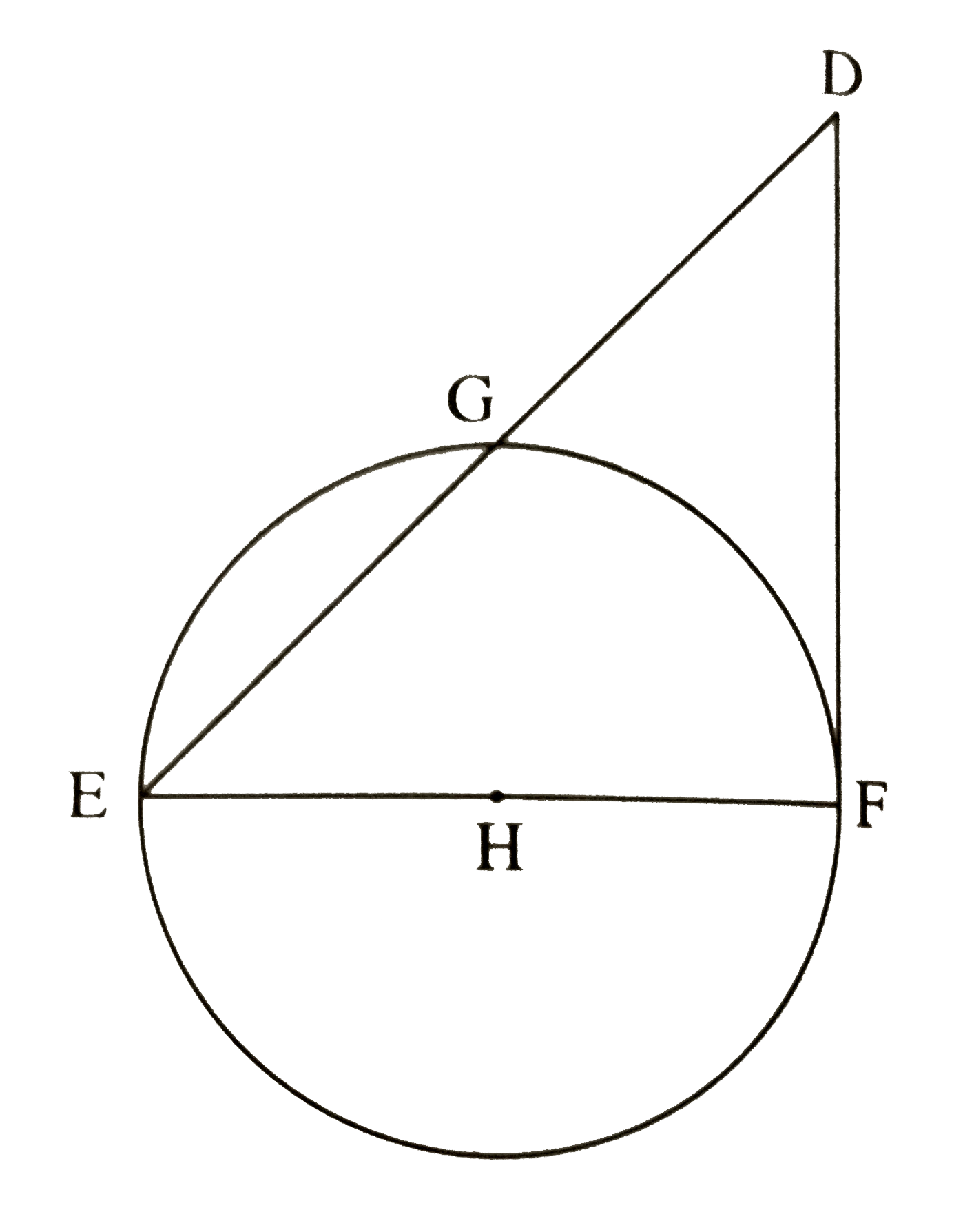 View Solution
View SolutionIn the adjoining figure, O is the centre of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB)=r. Prove that , □ ABOC is a square.
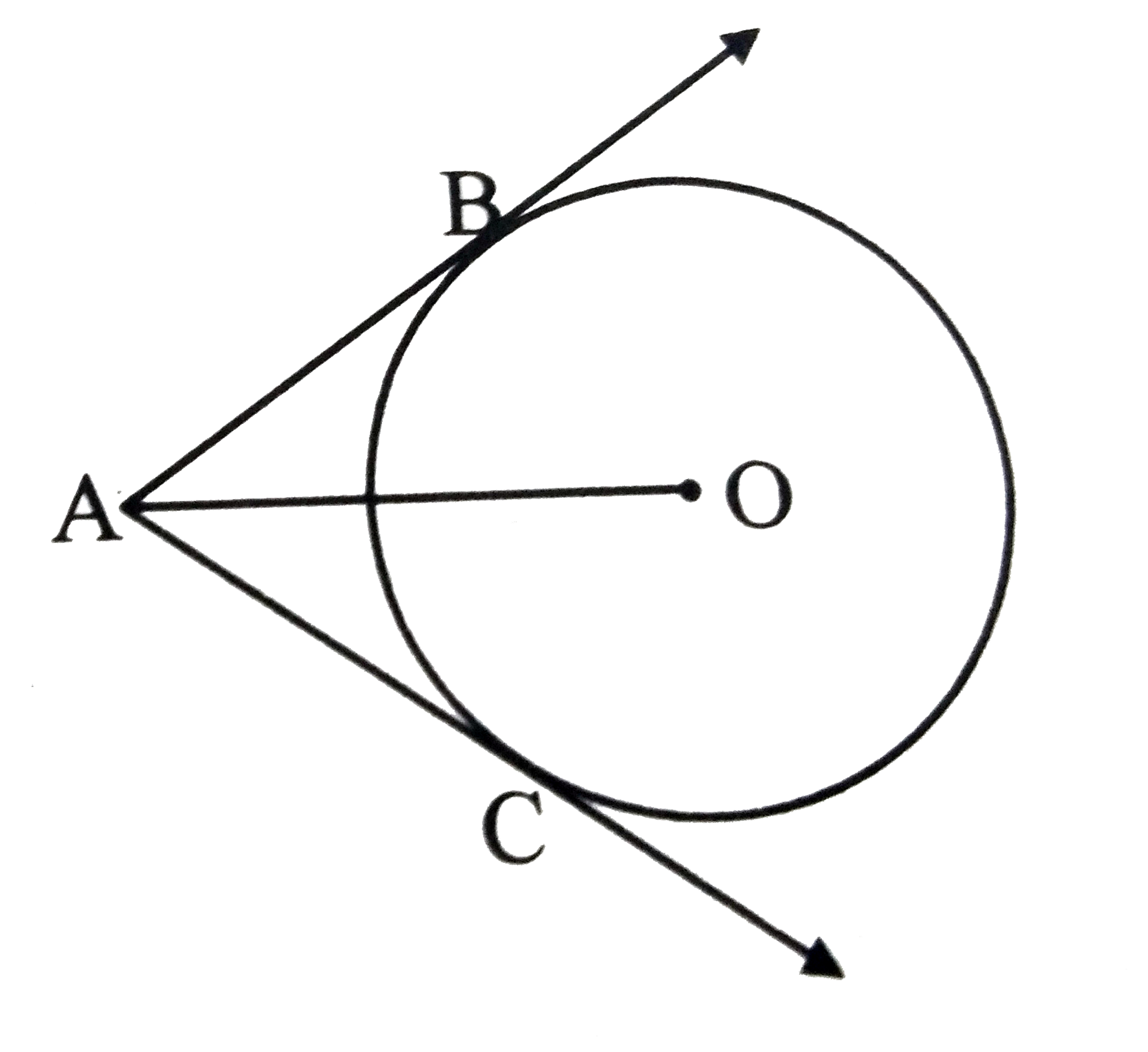 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the adjoining figure , AB is the diameter of a semicircle of maximum possible area . If the radius of the larger circle ( i.e, semicircle ) is r , the area of the inscribed circle is :
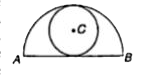 A5r2πB2π√3r2Cπr24Dnone of these
A5r2πB2π√3r2Cπr24Dnone of these
In the adjoining figure, seg RS is a diameter of the circle with centre O. Point T lies in the exterior of the circle. Prove that ∠RTS is an acute angle.
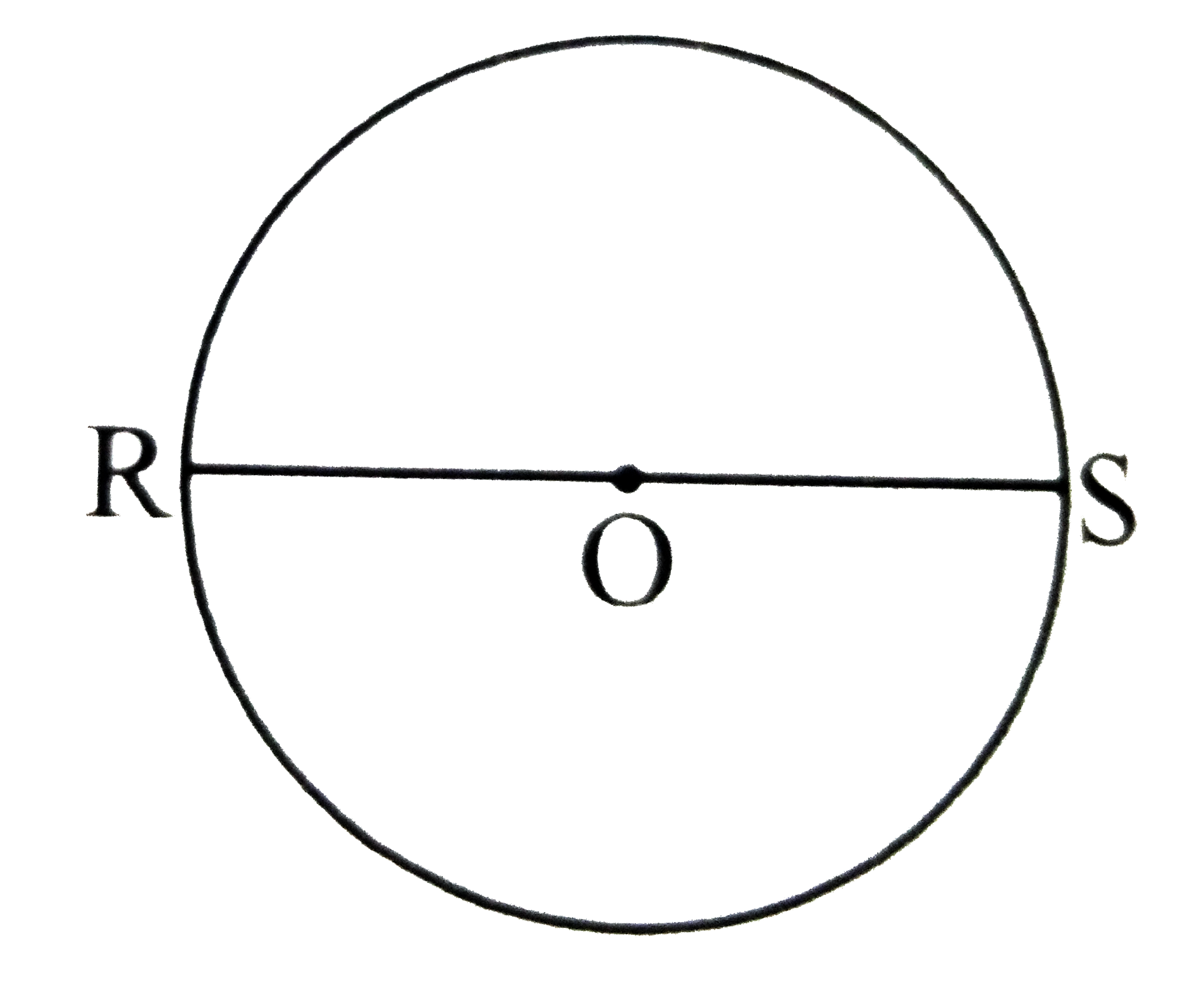 View Solution
View SolutionIn the adjoining figure, seg AB is a diameter of a circle with centre O. the bisector of ∠ACB intersects the circle at point D. Prove that ,seg AD≅segBD. Complete the following proof by filling the blanks.
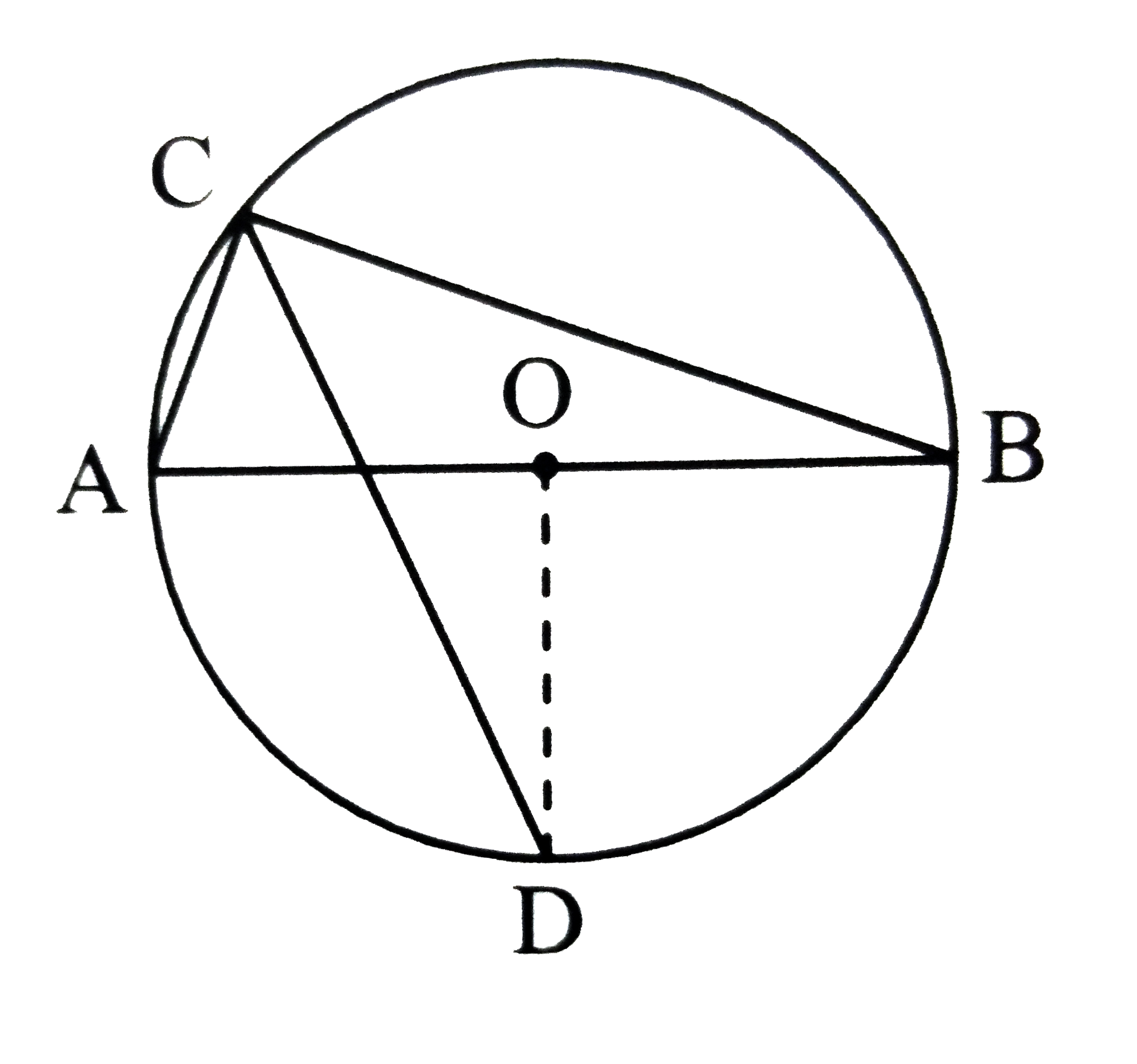 View Solution
View Solution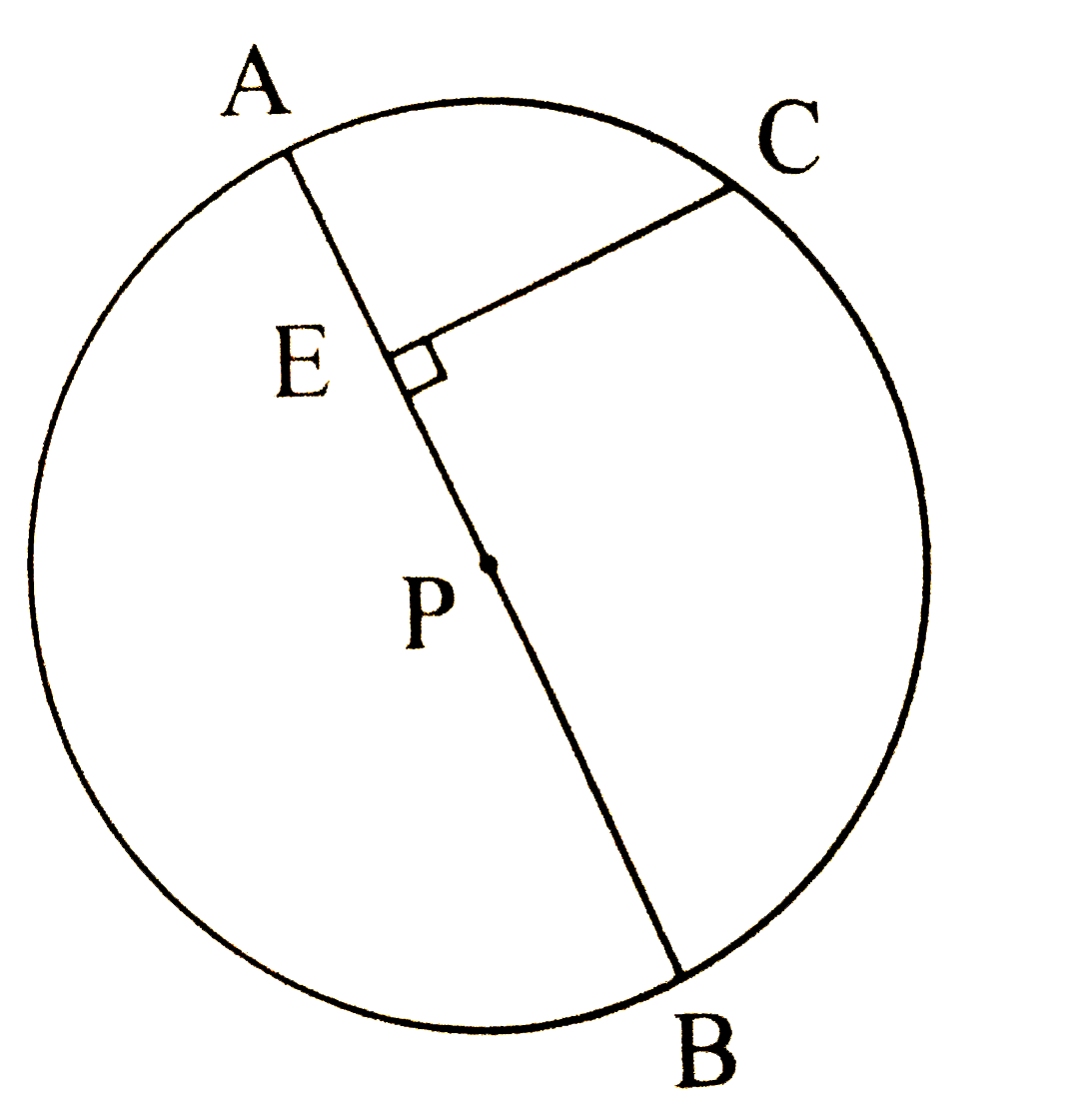
In the above figure, seg AB is a diameter of a circle with centre P.C is any point on the circle. Seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of folloing steps:
(a) Draw ray CE. It intersects the circle at D.
(b) Show that CE = ED.
Write the result using theorem of intersection of chords insides a circle.
(d) Using CE = ED, complete the proof.View SolutionThe diameter of a circle is a line which joins two points on the circle and also passes through the centre of the circle. (In the adjoining figure, AB is a diameter of the circle, C is its centre.) Express the diameter of the circle (d) in terms of its radius (r).
 View Solution
View SolutionIn the figure, O is the centre of the circle of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB)=r. Prove that, □ABOC is a square.
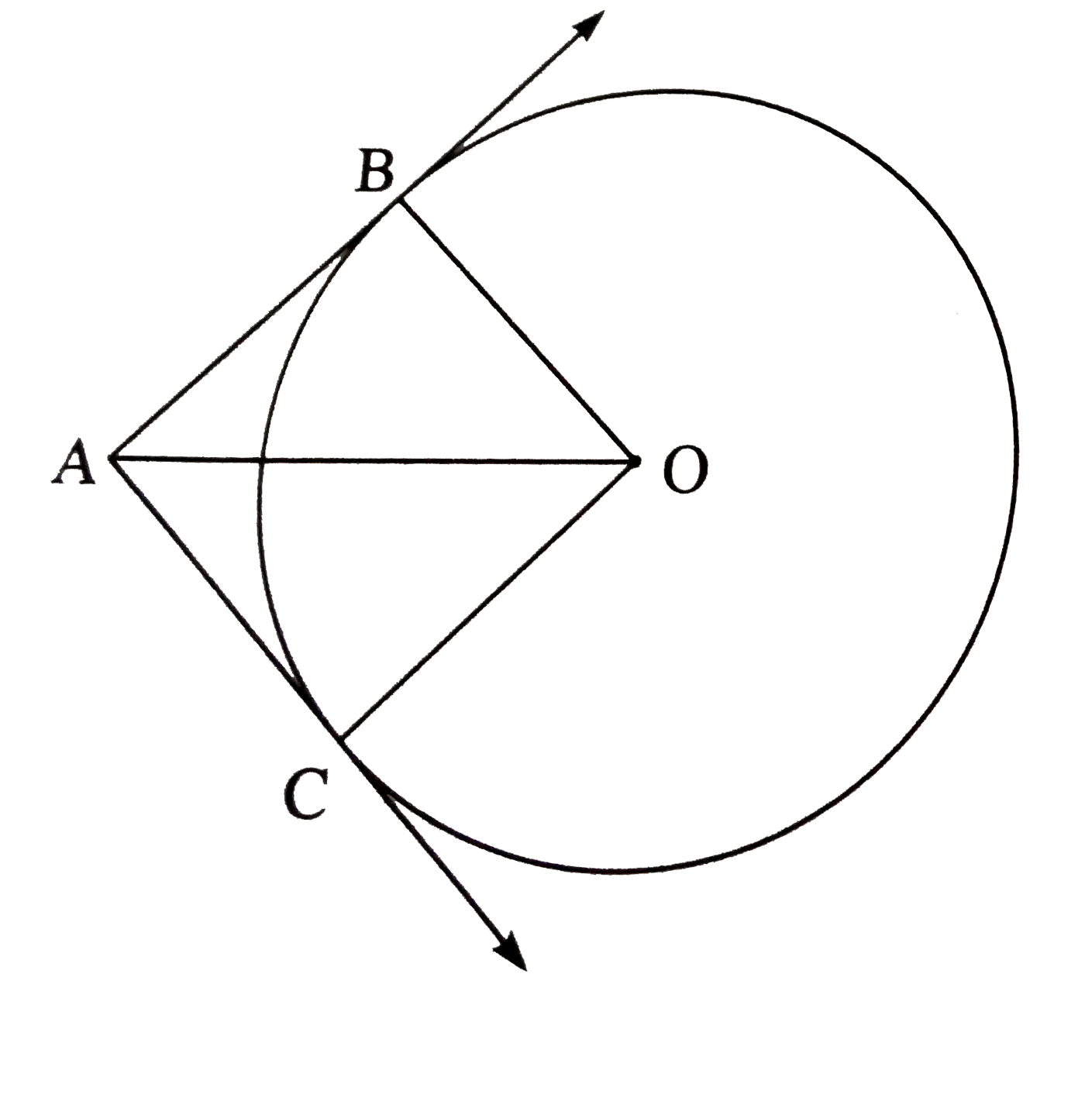 View Solution
View SolutionIn the adjoining figure, O is the centre and seg AB is a diameter. At the point C on the circle, the tangent CD is drawn. Line BD is a tangent to the circle at the point B. Show that segOD ∣∣ chord AC.
 View Solution
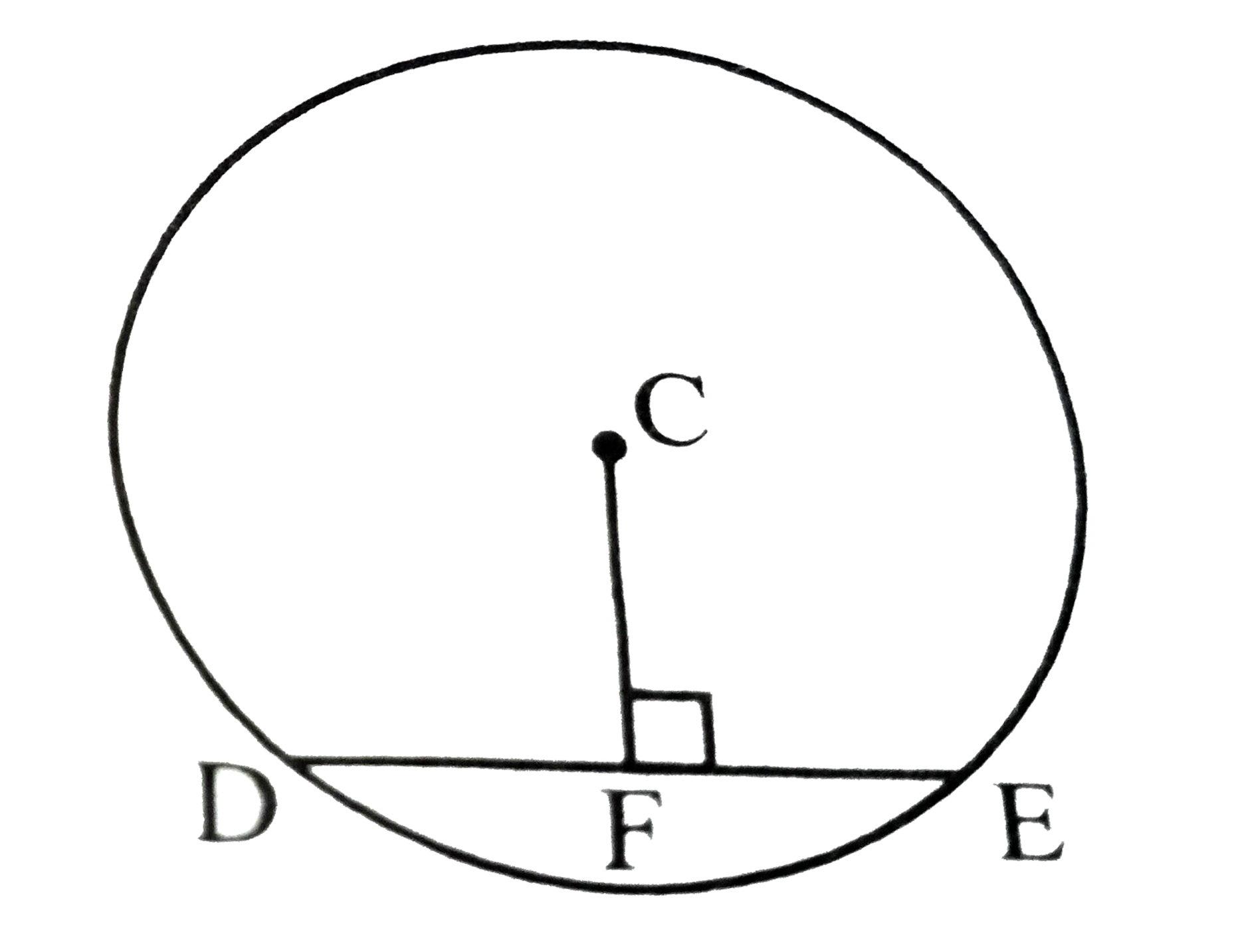
View SolutionIn the adjoining figure ,seg DE is a chord of a circle with centre C. seg CF ⊥ seg DE. If diameter of the circle is 20cm, DE=16cm, find CF. Recall and write theorems and properties which are useful to find the solution of the above problem. Using them solve the above problems.
 View Solution
View Solution

