In the adjoining figure, ABC is a triangle and D is any point in its interior. Show that BD+DC<AB+AC.
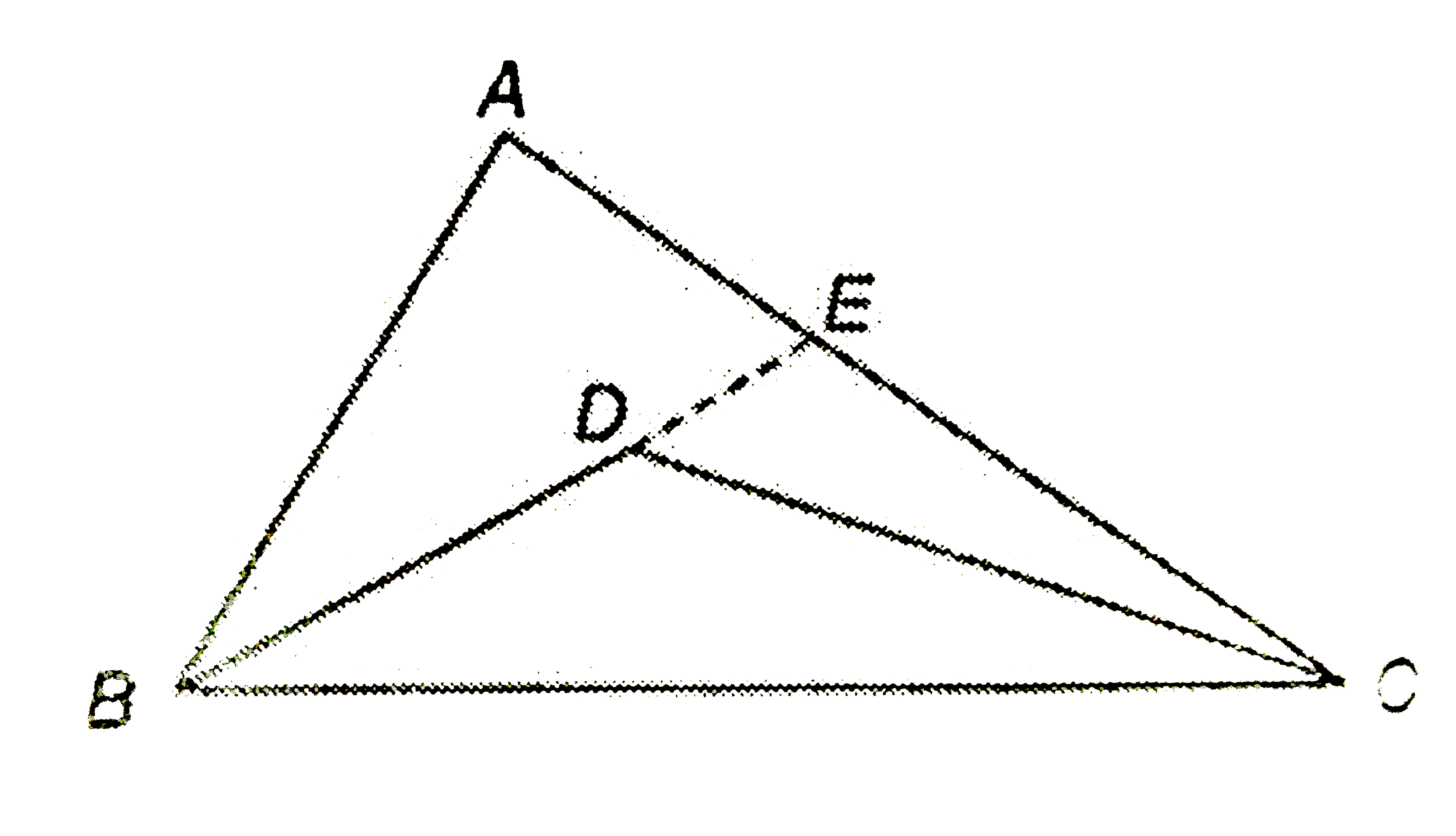
In ΔABE,
AB+AE>BE
(∵ sum of two sides of atriangle is greater than the third side)
⇒ AB+AE>BD+DE ...(1)
In ΔCDE,
DE+EC>DC ...(2)
(∵ sum of two sides of a triangle is greater than the third side)
Adding (1) and (2), we get
AB+AE+DE+EC>BD+DE+DC
⇒ AB+(AE+EC)>BD+DC
⇒ AB+AC>BD+DC Hence Proved.
Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Exercise 7a
35 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
In the adjoining figure, ABC is an isosceles triangle in which AB = AC. Also, D is a point such that BD = CD. Prove that AD bisects ∠A and ∠D
View SolutionIn the adjoinng figure, ΔABC is an isoceless triangle in which AB = AC. Also, D is a point such that BD = CD. Prove that AD bisects ∠Aand∠D.
View Solution
Knowledge Check
D is any point on side AC of a ΔABC with AB=AC then
ACD<BDBCD=BDCCD>BDDNONE
In the adjoining figure, E is a point on the median AD of a ΔABC. Show that ar (ΔABE)=(ΔACE).
View SolutionIn △ABC,AB>AC and D is any point on BC. Prove that, AB > AD.
View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) AB+BC+CD+DA<2(AC+BD)
(b) AB+BC+CD+DA>(AC+BD)

View SolutionIn the adjoining figure, ABC is a triangle in whcich AB=AC. If D and E are poitns on AB and AC respecrtively such that AD=AE, show that the points B,C,E and D are concyclic.
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
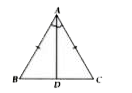
BD = CD
View SolutionIn the figure given below ABC is a triangle right angled at A and AC ⊥ BD . Show that
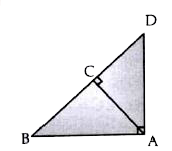
AD2=BD×DC
View SolutionABC is a triangle in which AB=AC and D is any point in BC . Prove that AB2−AD2=BDCD .
View Solution
