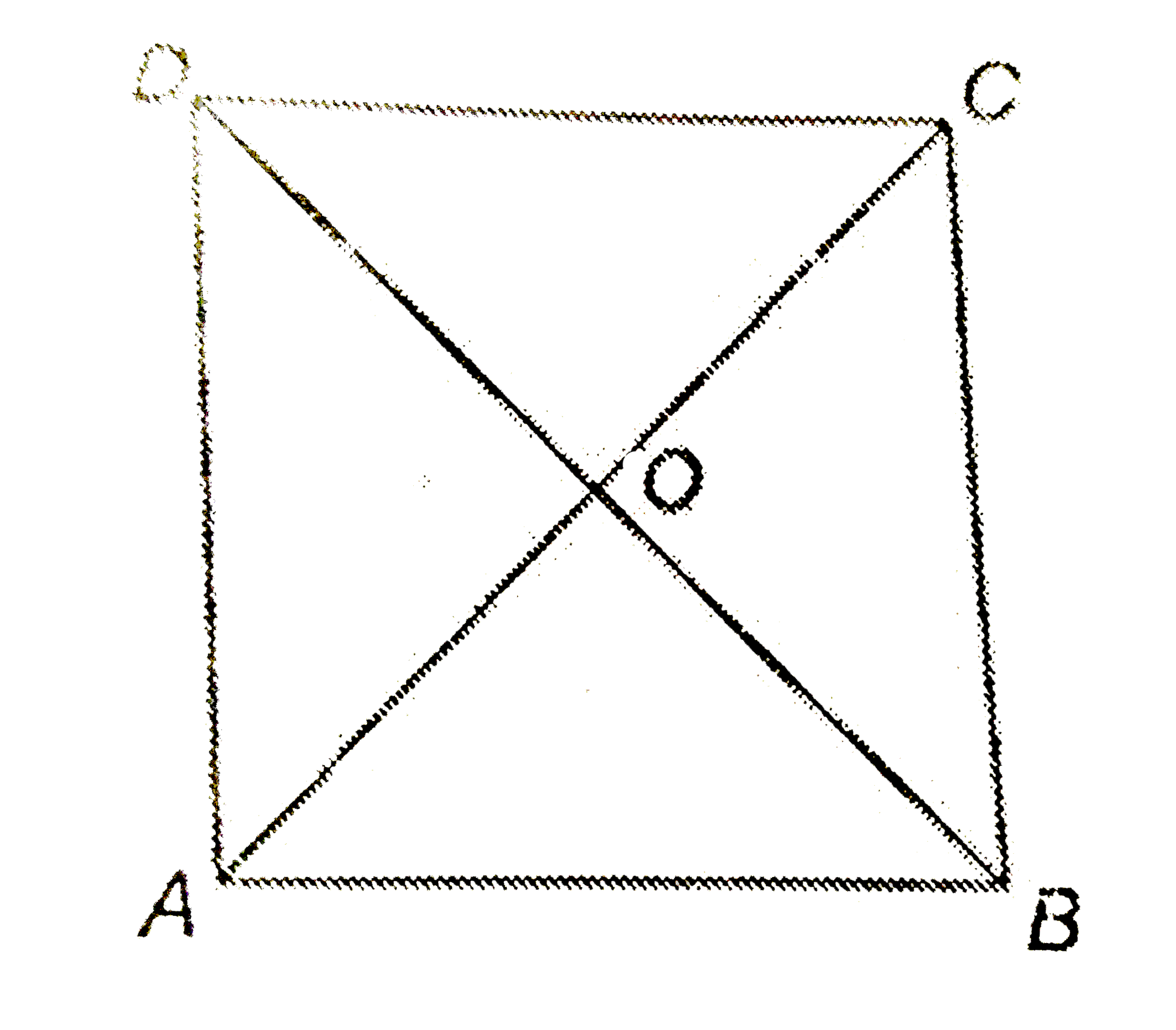
In the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a)
(b)

(a) We know that the sum of any two sides of a triangle is greater than the third side.
(b)
Adding (5), (6), (7) and (8), we get
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar5videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Exercise 7a35videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)10videos
SURFACE AREA AND VOLUME
Similar Questions
If ABCD is a quadrilateral whose diagonals AC and BD intersect at O, then
 View Solution
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect point O. Prove that :
AB+BC+CD+DA<2(AC+BD)
 View Solution
View SolutionABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
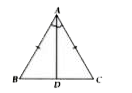
BD = CDView SolutionABCD is quadrilateral. Is AB+BC+CD+DA<2(AC+BD)?
View SolutionABCD is a quadri,aterial prove that (AB+BC+CD+DA)>(AC+BD)
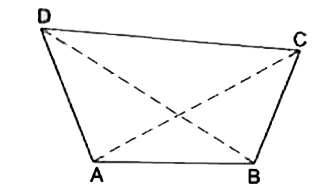 View Solution
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
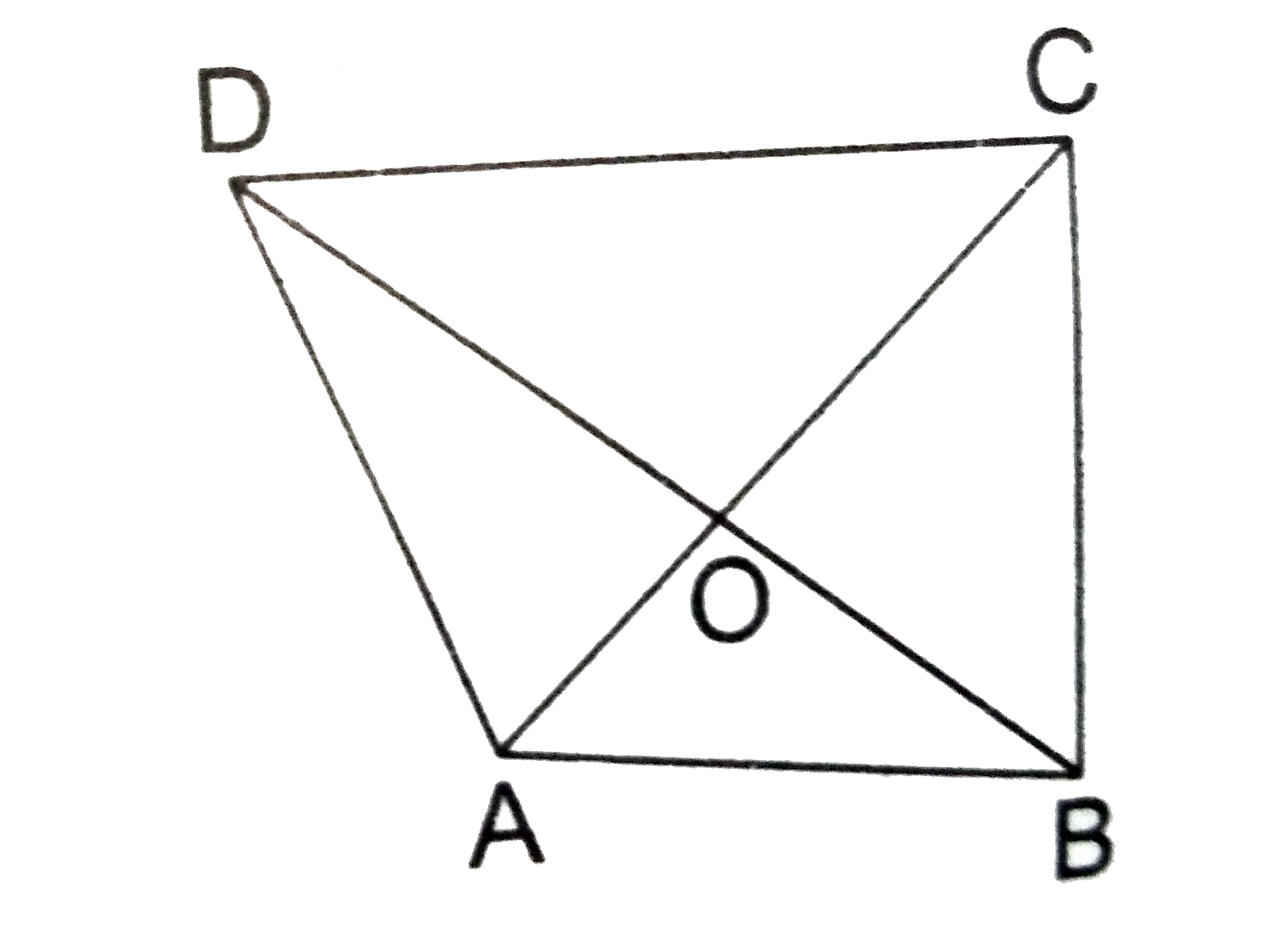 View Solution
View SolutionIn a quadrilateral ABCD, show that
(AB+BC+CD+DA)>(AC+BD).View SolutionShow that in a quadrilateral ABCD AB+BC+CD+DA>AC+BD
View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).
 View Solution
View Solution

