In the adjoining figure, BD = CE and ∠ADB=∠AEC=90∘, prove that
(i) ΔABD≅ΔACE (ii) ABC is an isosceles triangle.

(i) In ΔABD and ΔACE,
∵⎧⎪⎨⎪⎩∠3=∠3(common)∠1=∠2(each 90∘, given)BD=CE(given)
∴ΔABD≅ΔACE (AAS) Hence Proved.
(ii) AB=AC (c.p.c.t)
Hence, ΔABC is an isosceles triangle. Hence Proved.
Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Exercise 7a
35 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
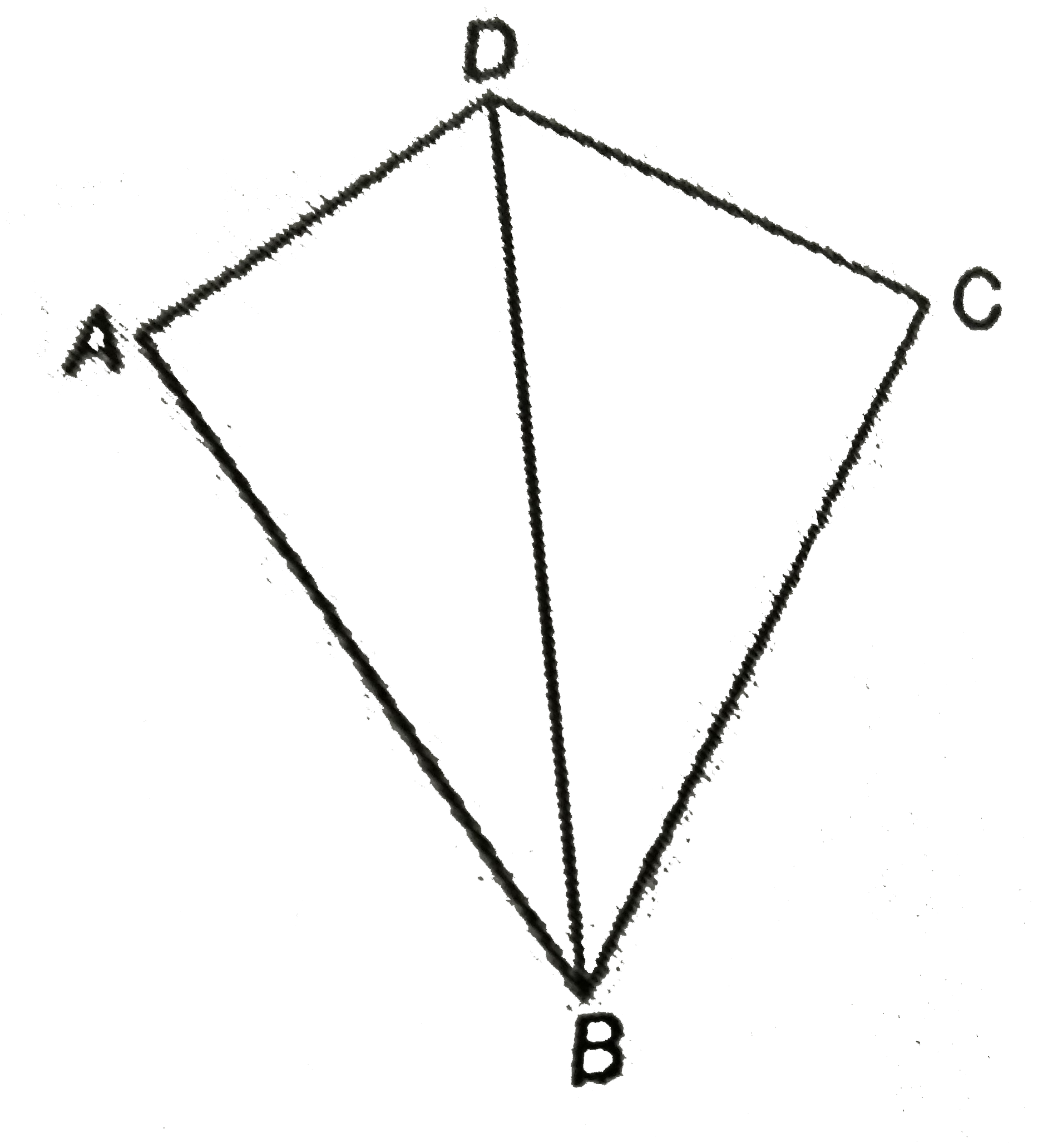
In the adjoining figure, ∠BAC=∠BDC and ∠ABC=∠BCD. Prove that :
(i) ΔABC≅ΔDCB
(ii) ΔABE≅ΔDCF.

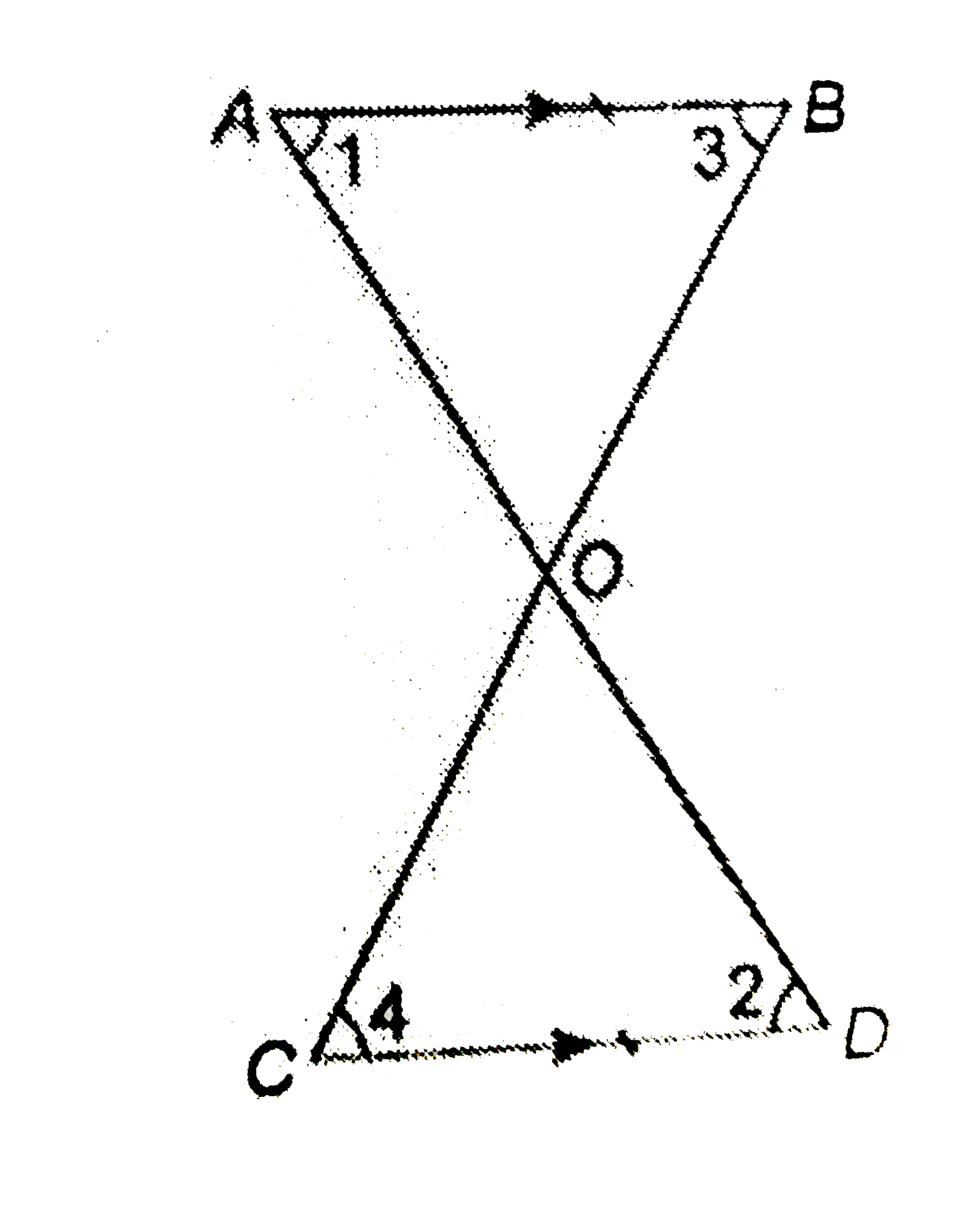
View SolutionIn the adjoining figure, AB = CD and AB||CD prove that
(i) ΔAOB≅ΔDOC
(ii) AD and BC bisect each other at the point O.
View SolutionIn the adjoining figure, AD=DC and bisects ∠ADC. Prove that ΔADB≅ΔCDB.
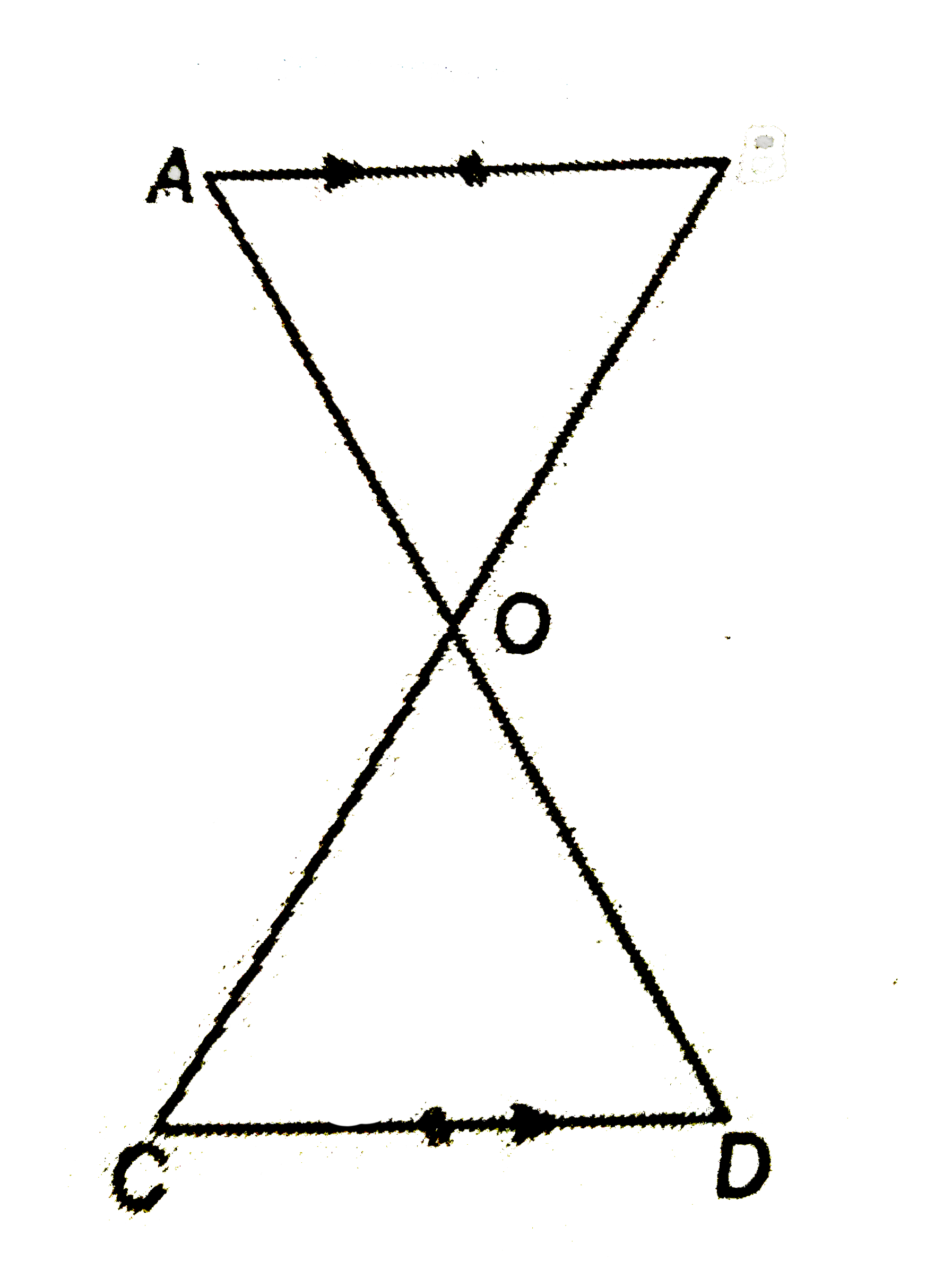
View SolutionIn the adjoining figure AB=CD and AB||CD prove that :
(i) ΔAOB≅ΔDOG
(ii) AD and BC bisect each other at point O.
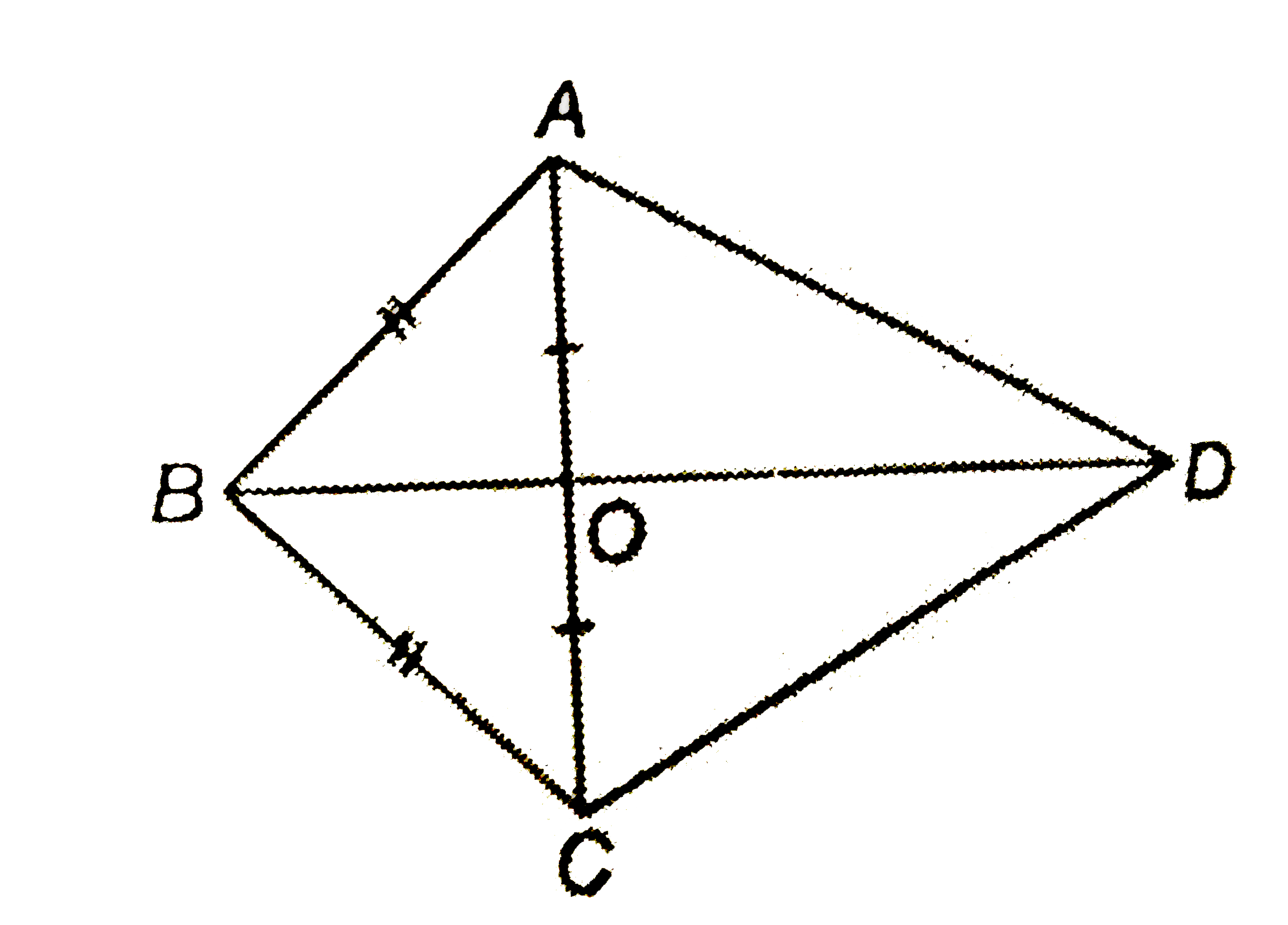
View SolutionIn the following figure, OA = OC and AB = BC. Prove that :
(i) ∠APB=90∘
(ii) ΔAOD≅ΔCOD
(iii) AD=CD
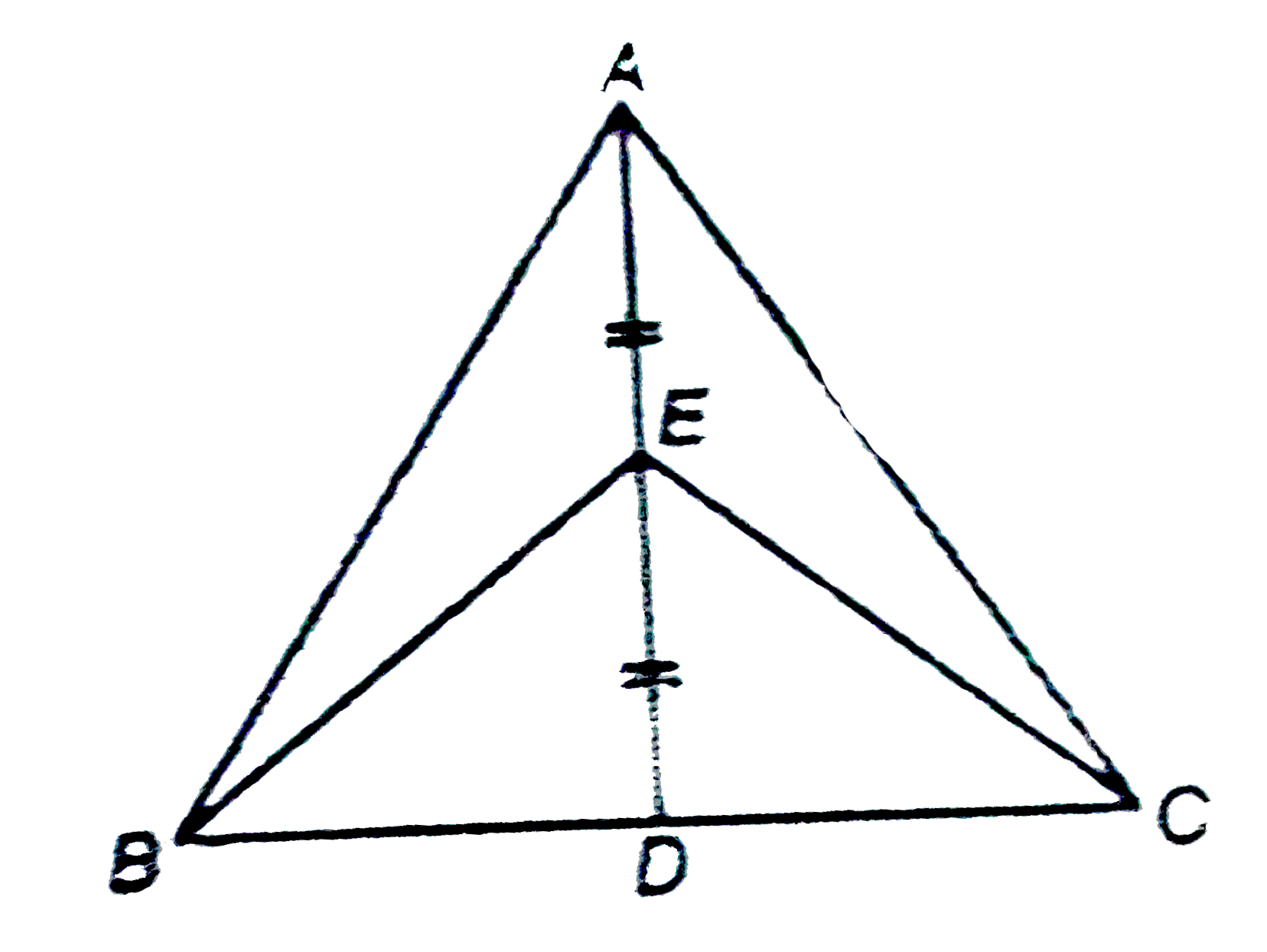
View SolutionIn the adjoining figure, BD = DC and AE = ED. Prove that
area of ΔACE=14 area of ΔABC
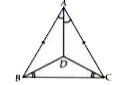
View SolutionIn the adjoining figure, prove that ΔABD≅ΔACD,
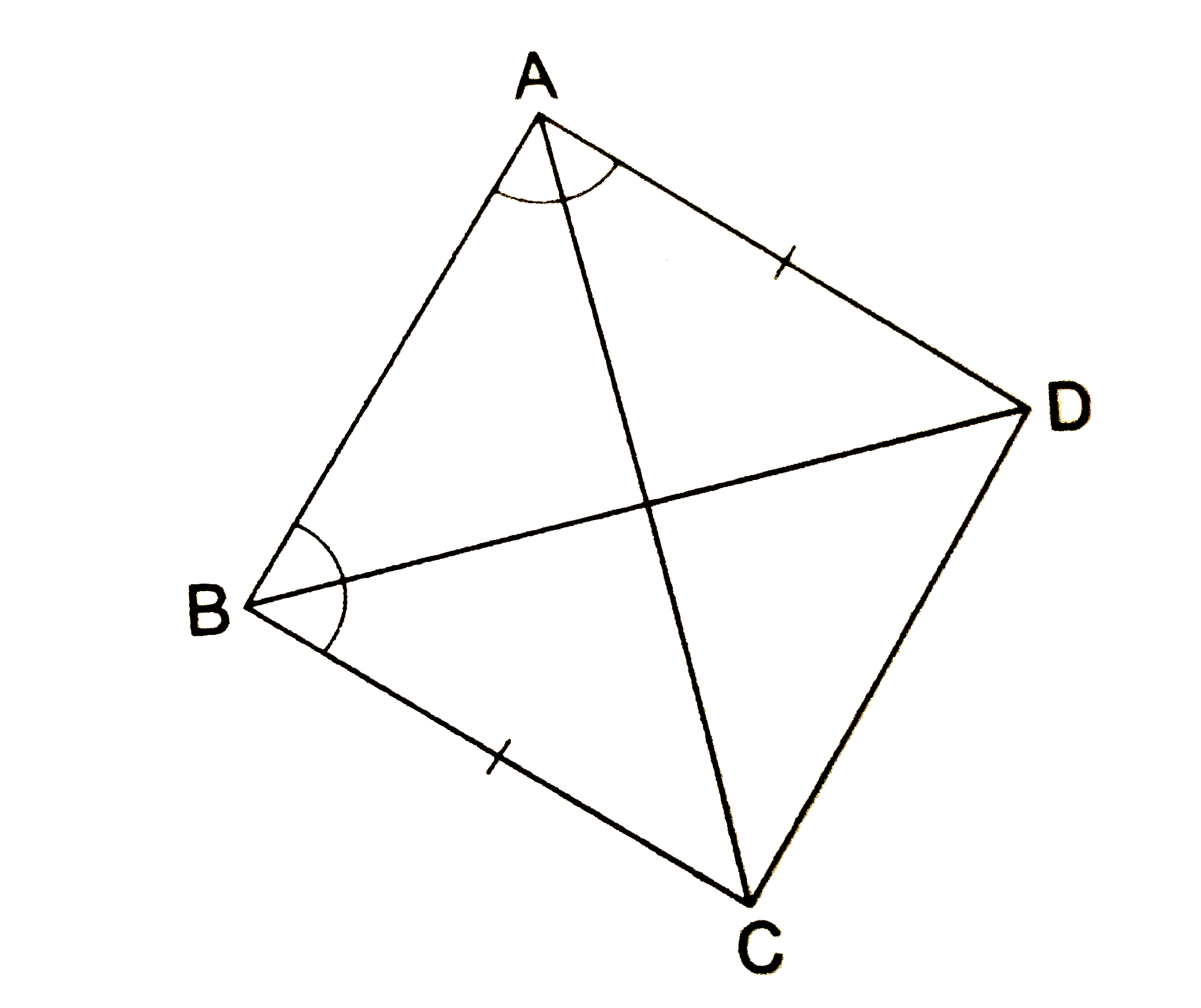
View SolutionIn the given figure, ABCD is a quadrilateral in which AD = BC and ∠DAB=∠CBA.
Prove that (i) ΔABD≅ΔBAC,
(ii) BD = AC,
(iii) ∠ABD=∠BAC.
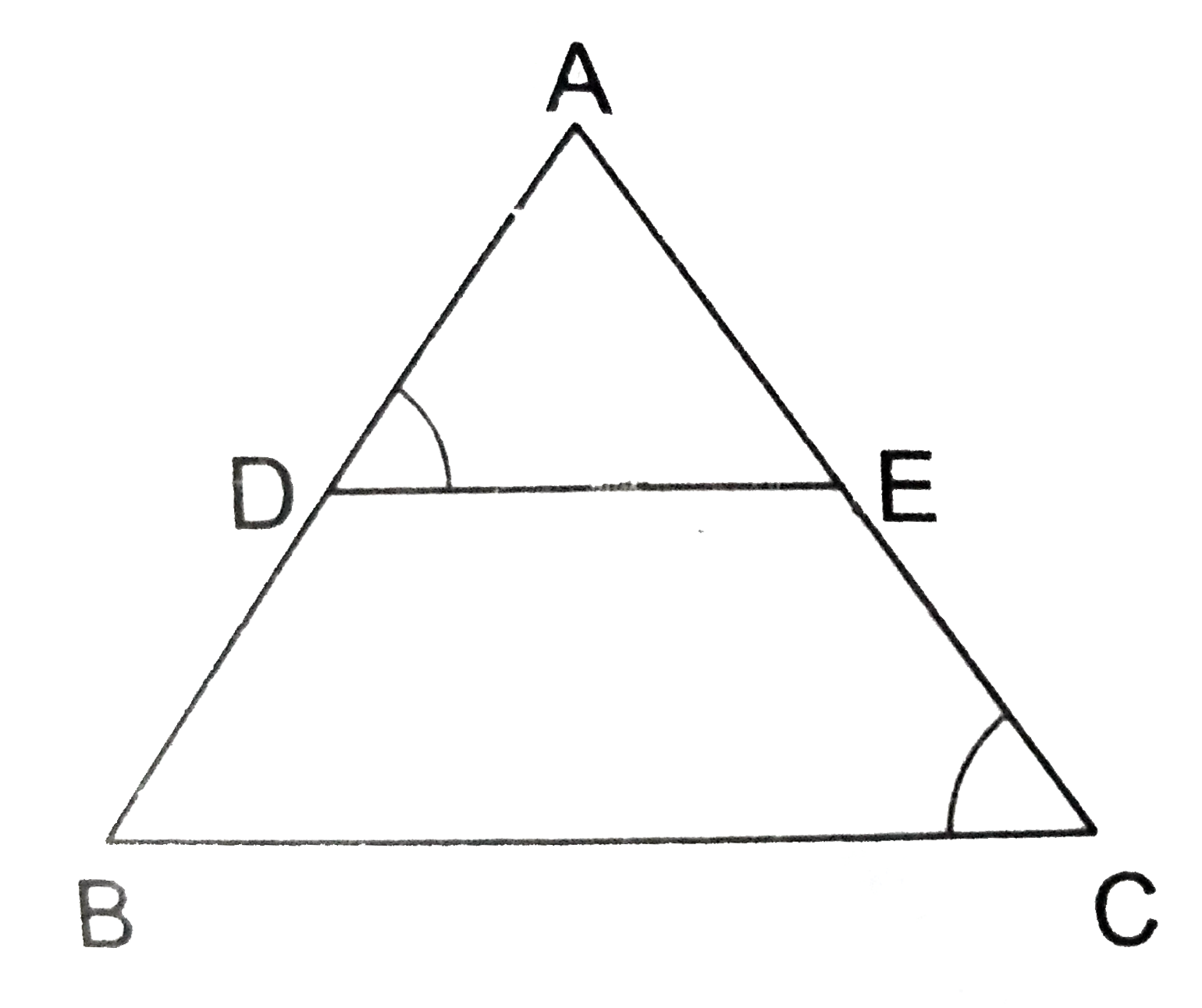
View SolutionIn the given figure, ADDB=AEEC and ∠ADE=∠ACB. Prove that ΔABC is an isosceles triangle.
View SolutionIn a tringle ABC, AB = AC and bisector of angle A meets BC at D. Prove that :
(i) ΔABD≅ΔACD (ii) AD is perpendicular to BC.
View Solution
