In the adjoining figure, ΔABC is an isosceles triangle in which AB = AC. Side CP is parallel to AB and AP is the bisector of exterior angle CAD of Δ ABC. Prove that ∠PAC=∠BCAand□ABCP is a parallelogram.
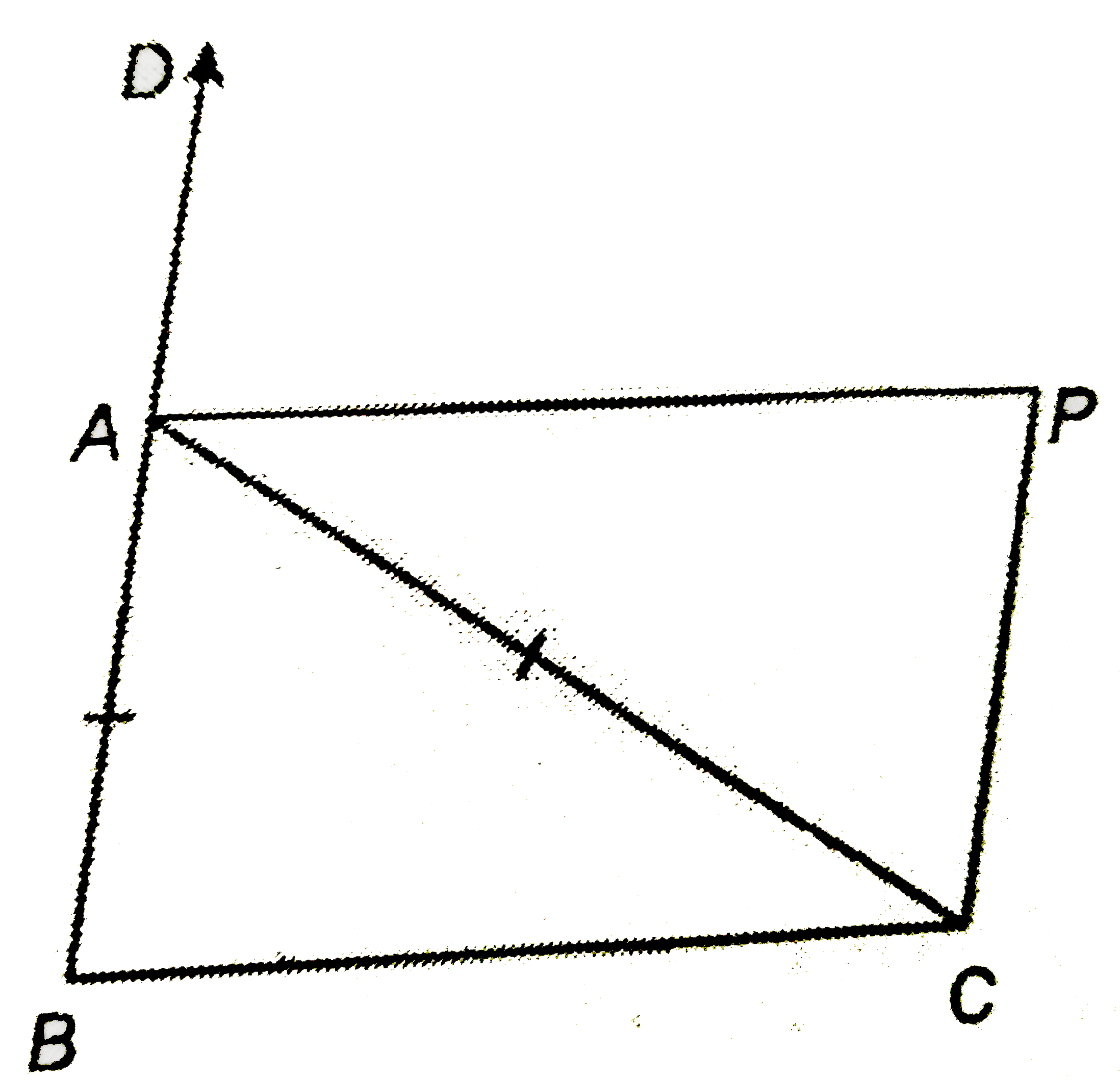
Step by step video & image solution for In the adjoining figure, DeltaABC is an isosceles triangle in which AB = AC. Side CP is parallel to AB and AP is the bisector of exterior angle CAD of Delta ABC. Prove that anglePAC=angleBCAand squareABCP is a parallelogram. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8b
15 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar
11 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
In Figure, ABC is an isosceles triangle in which AB=AC.andCP∣∣AB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.
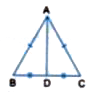
View SolutionIn the adjoining figure, ΔABC is an isosceles triangles in which AB=AC and AD is a median. Prove that :
(i) ΔADB≅ΔADC
(ii) ∠BAD=∠CAD
View SolutionIn the adjoining figure, ΔABC is an isosceles triangles in which AB=AC and AD is the bisector of ∠A. Prove that :
(i) ΔADB≅ΔADC
(ii) ∠B=∠C
(iii) BD=DC
(iv) AD⊥BC

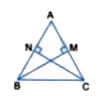
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB=AC. If BM⊥AC and CN⊥AB, prove that :
(i) ΔBMC≅ΔCNB
(ii) BM=CN
View SolutionABC is an isosceles triangle in which AB = AC . AP bisects exterior angle DAC and CP II AB . Show that angle PAC = Angle BCA (ii) ABCP is a Parallelogram
View SolutionIf ΔABC is an isosceles triangle with AB = AC. Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
View Solution△ABC is an isosceles triangle with AC = BC. If AB2=2AC2 . Prove that △ABC is a right triangle.
View SolutionThe tangent to the circumcircle of an isosceles ΔABC at A, in which AB= AC, is parallel to BC.
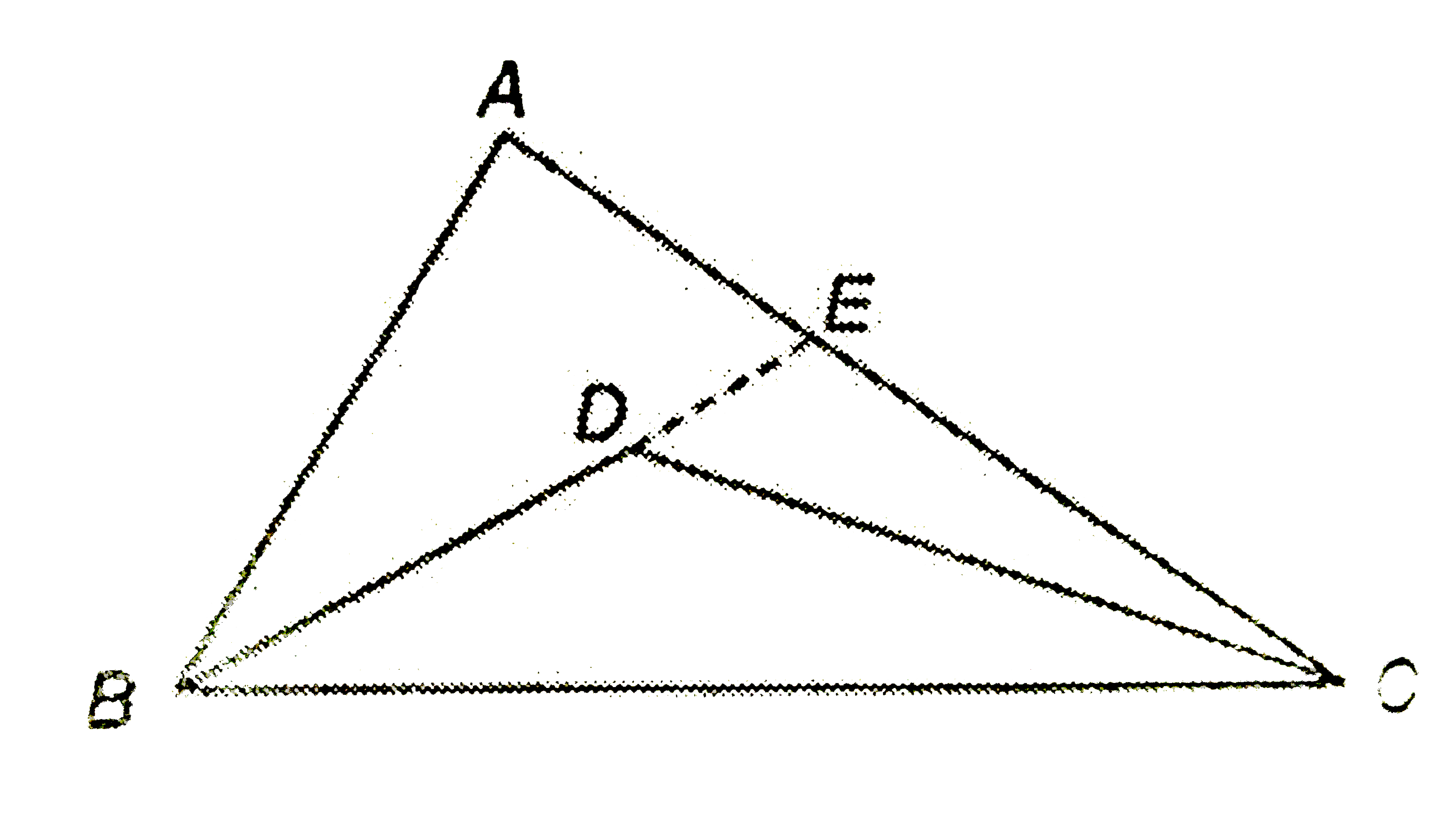
View SolutionIn the adjoining figure, ABC is a triangle and D is any point in its interior. Show that BD+DC<AB+AC.
View SolutionThe following figure shows a triangle ABC in which AB=AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that
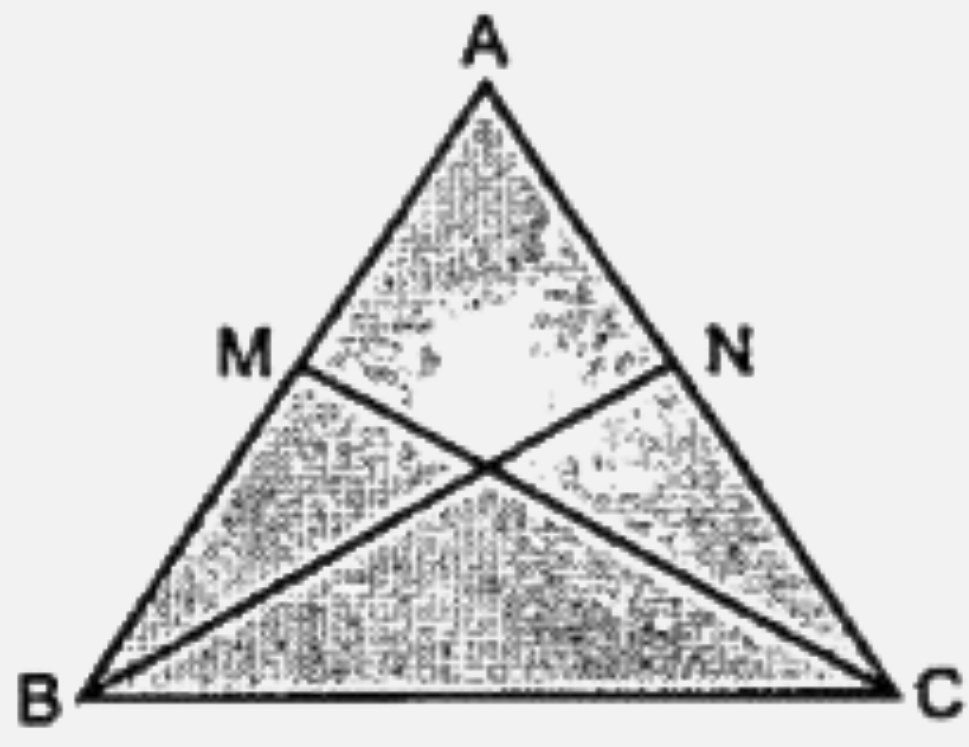
AM=AN
View Solution
