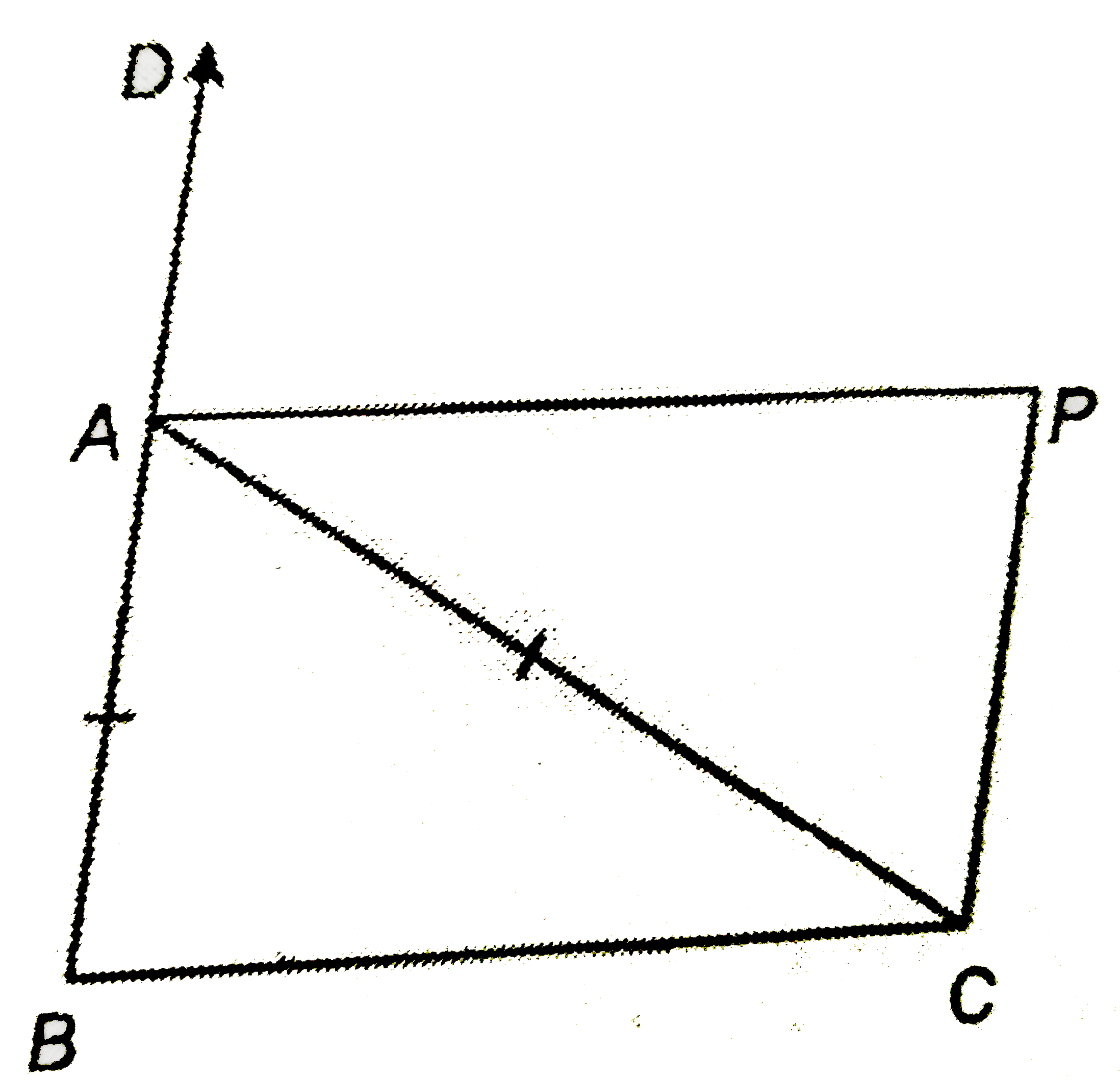
ABC is an isosceles triangle in which AB = AC . AP bisects exterior angle DAC and CP II AB . Show that angle PAC = Angle BCA (ii) ABCP is a Parallelogram
Step by step video & image solution for ABC is an isosceles triangle in which AB = AC . AP bisects exterior angle DAC and CP II AB . Show that angle PAC = Angle BCA (ii) ABCP is a Parallelogram by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ABC is an isosceles triangle in which AB=AC. AD bisects exterior angle PAC and CD∣∣AB. Show that(i) ∠DAC=∠BCA and (ii) ABCD is a parallelogram.
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC. Side CP is parallel to AB and AP is the bisector of exterior angle CAD of Δ ABC. Prove that ∠PAC=∠BCAand□ABCP is a parallelogram.
View SolutionABC is an isosceles triangle with AB =AC and BD,CE are its two medians. Show that BD=CE .
View SolutionIn the given figure, AB//EC,AB=ACandAE bisects ∠DAC. Prove that:
(i) ∠EAC=∠ACB
(ii) ABCE is a parallelogram.
 .
.
View SolutionABC is a right triangle with AB = AC.If bisector of ∠A meet BC at D then prove that BC =2 AD .
View Solution△ABC is an isosceles triangle with AC = BC. If AB2=2AC2 . Prove that △ABC is a right triangle.
View SolutionABCD is a quadrilateral in which AB=BC and AD=CD ,Show that BD bisects both the ∠ABC and ∠ADC.
View SolutionConstruct an isosceles ΔABC such that AB=AC=5cmand∠A=60∘.
View SolutionOn the sides AB and AC of triangle ABC, equilateral triangles ABD and ACE are drawn. Prove that :
(i) ∠CAD=∠BAE
(ii) CD = BE
View SolutionABCDE is a pentagon in which AB = AE, BC = ED and ∠ABC=∠AED.
Prove that
AC= AD
(ii) ∠BCD=∠EDC
View Solution
