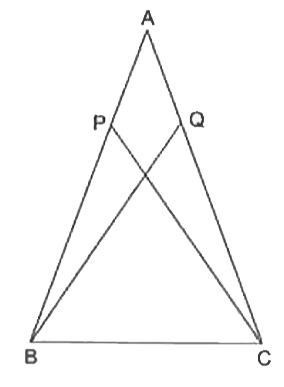
In the adjoining figure, P and Q are two points on equal sides AB and AC of a isosceles triangle ABC such that AP = AQ, then
BQ = CP
∠ABQ=∠ACP
∠BAQ=∠CPA
both (a) and (b)
The correct Answer is:D
Step by step video, text & image solution for In the adjoining figure, P and Q are two points on equal sides AB and AC of a isosceles triangle ABC such that AP = AQ, then by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Match the following2videos
CONGRUENCE OF TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Assertion & Reaction Type5videos
CONGRUENCE OF TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - NCERT Section (Exercise 7.2)20videos
CONGRUENCE OF TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - COMPARING QUANTITIES EXERCISE - Olympaid/HOTS Corner20videos
COMPARING QUANTITIES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - DATA HANDLINGEXERCISE - Olympiad / Hots Corner20videos
DATA HANDLING
Similar Questions
Knowledge Check
- Question 1 - Select One
If the radius of the circum-circle of an isosceles triangle ABC is equal to AB(=AC), then angle A is
Aπ6Bπ3Cπ2D2π3
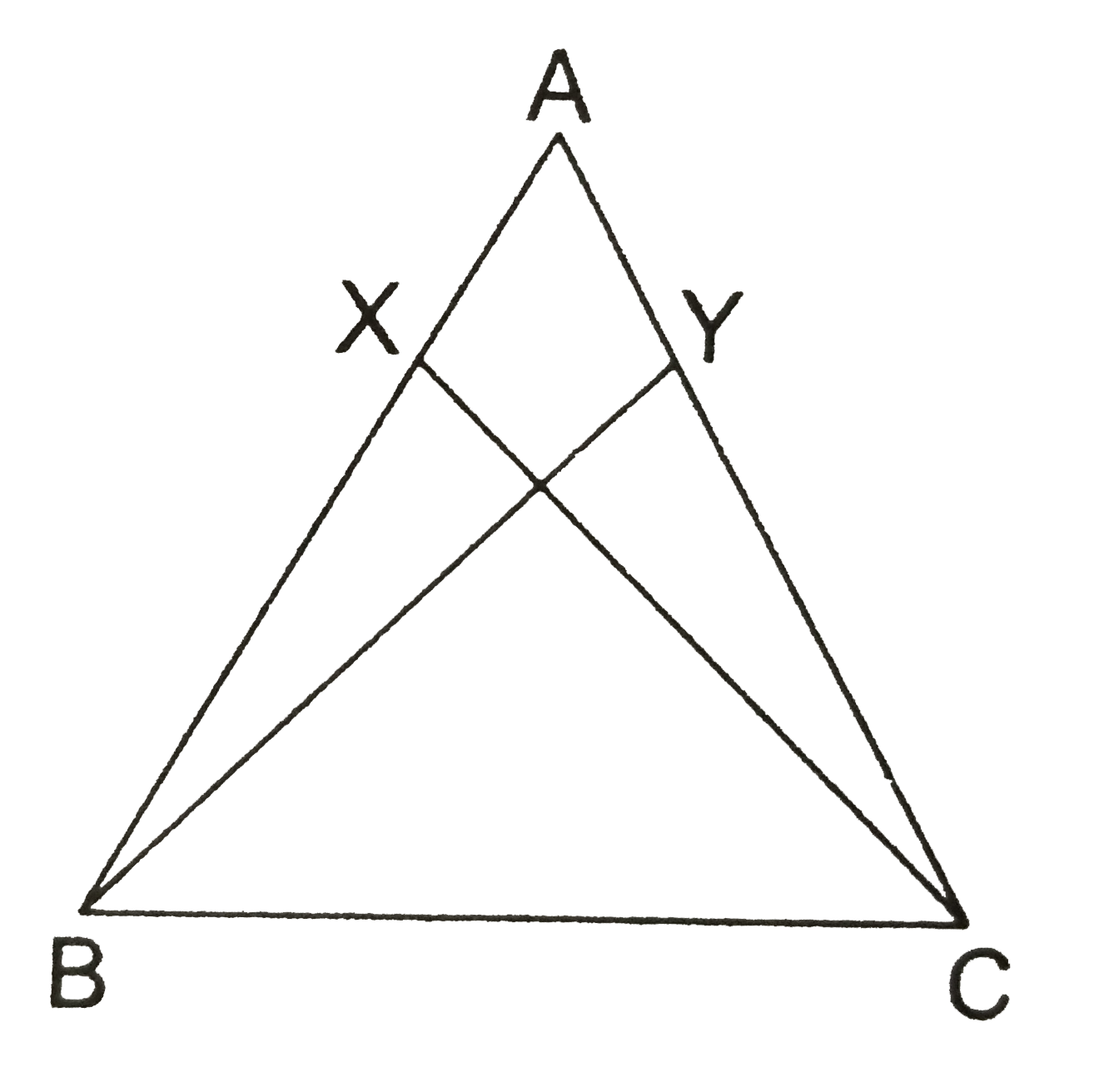
In the adjoining figure, X and Y are respectively two points on equal sides AB and AC of ΔABC such that AX = AY. Prove that CX = BY.
 View Solution
View SolutionDandE are points on equal sides ABandAC of an isosceles triangle ABC such that AD=AE . Prove that B,C,D,E are concylic.
View SolutionD and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD=AE. Prove that B, C, D, E are concyclic.
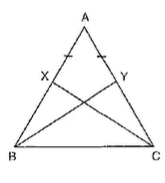
View SolutionIn Figure, X and Y are two points on equal sides AB and AC of a ABC such that AX=AY. Prove that XC=YB.
View SolutionIn Figure, X, Y are two points on equal sides AB and AC of a ABC such that AX=AY. Prove that XC=YB
 View Solution
View SolutionIn the adjoining figure D, E and F are the mid - points of the sides BC, AC and AB respectively to triangle. Show that ∠EDF=∠A, ∠DEF=∠B and ∠DFE=∠C:
 View Solution
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, AC and AB respectively. △DEF is congruent to triangle :
 View Solution
View Solution