In the adjoining figure the circles with centers P and Q touch each other at R . A line passing through R meets the circles at A and B respectively then
Prove that :
(i) seg seg BQ.
(ii) .
(iii) Find if
 Solution in Tamil
Solution in Tamil
The correct Answer is:
Step by step video & image solution for In the adjoining figure the circles with centers P and Q touch each other at R . A line passing through R meets the circles at A and B respectively then Prove that : (i) seg AP|| seg BQ. (ii) DeltaAPR~DeltaRQB . (iii) Find angleRQB if anglePAR = 35^(@) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - CHETAN PUBLICATIONCHAPTER - CIRCLEEXERCISE - Practice Set - 3.3
3 Videos
- CIRCLEBOOK - CHETAN PUBLICATIONCHAPTER - CIRCLEEXERCISE - Practice Set - 3.4
7 Videos
- CIRCLEBOOK - CHETAN PUBLICATIONCHAPTER - CIRCLEEXERCISE - Assignment - 3 (Solve any two of the following questions):
3 Videos
- CHALLENGING QUESTIONSBOOK - CHETAN PUBLICATIONCHAPTER - CHALLENGING QUESTIONSEXERCISE - Mensuration
9 Videos
- CO-ORDINATE GEOMETRY BOOK - CHETAN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - ASSIGNMENT-5
11 Videos
Similar Questions
In the adjoining figure, G, D, E, F are concyclic points of a circle with centre C . ∠ECF=70∘ m (arc DGF) =200∘ find
(i) m arc DE
(iii) m (arc DEF).

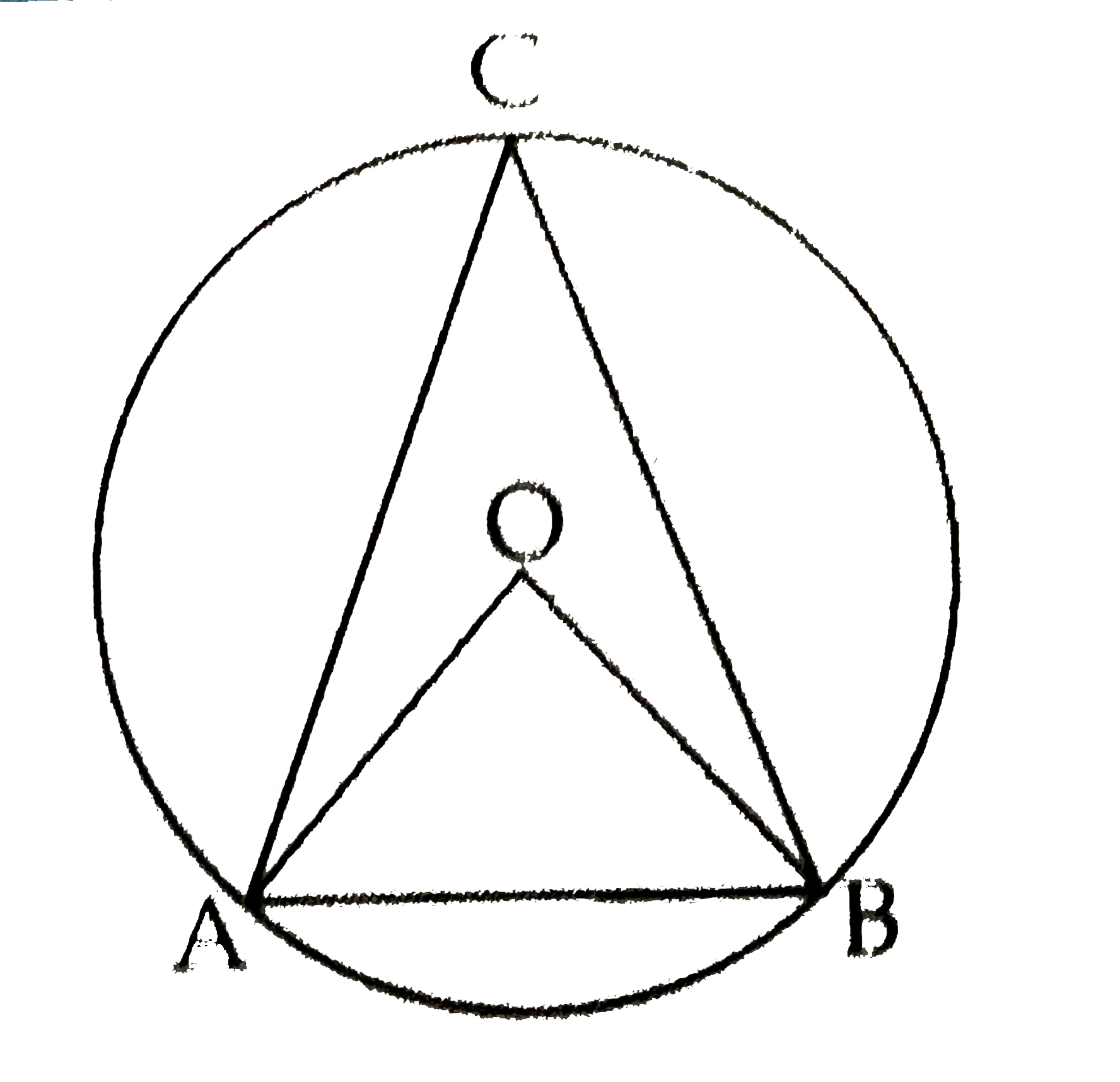
View SolutionIn the abjoining figure, point O is the centre of the circle . Length of chord AB is equal to the radius of the circle . Find
(i) ∠AOB
(ii) ∠ACB
(iii) nm (arc AB)
(iv) m (arc ACB)
View SolutionA circle with centre 'O' is incircle of ΔABC.ΔBCA=90∘ . Radius of the circle is r.
Prove that : 2r = a + b - c.

View SolutionA tin maker converts a cubical metalic box into 10 cylindrical tins. Side of the cube is 50 cm and radius of the cylindrical is 7cm. Find the height of each cylinder so made if the wastage incurred was 12%. (π=227)
View SolutionSlope of a line is √3. Find its inclination.
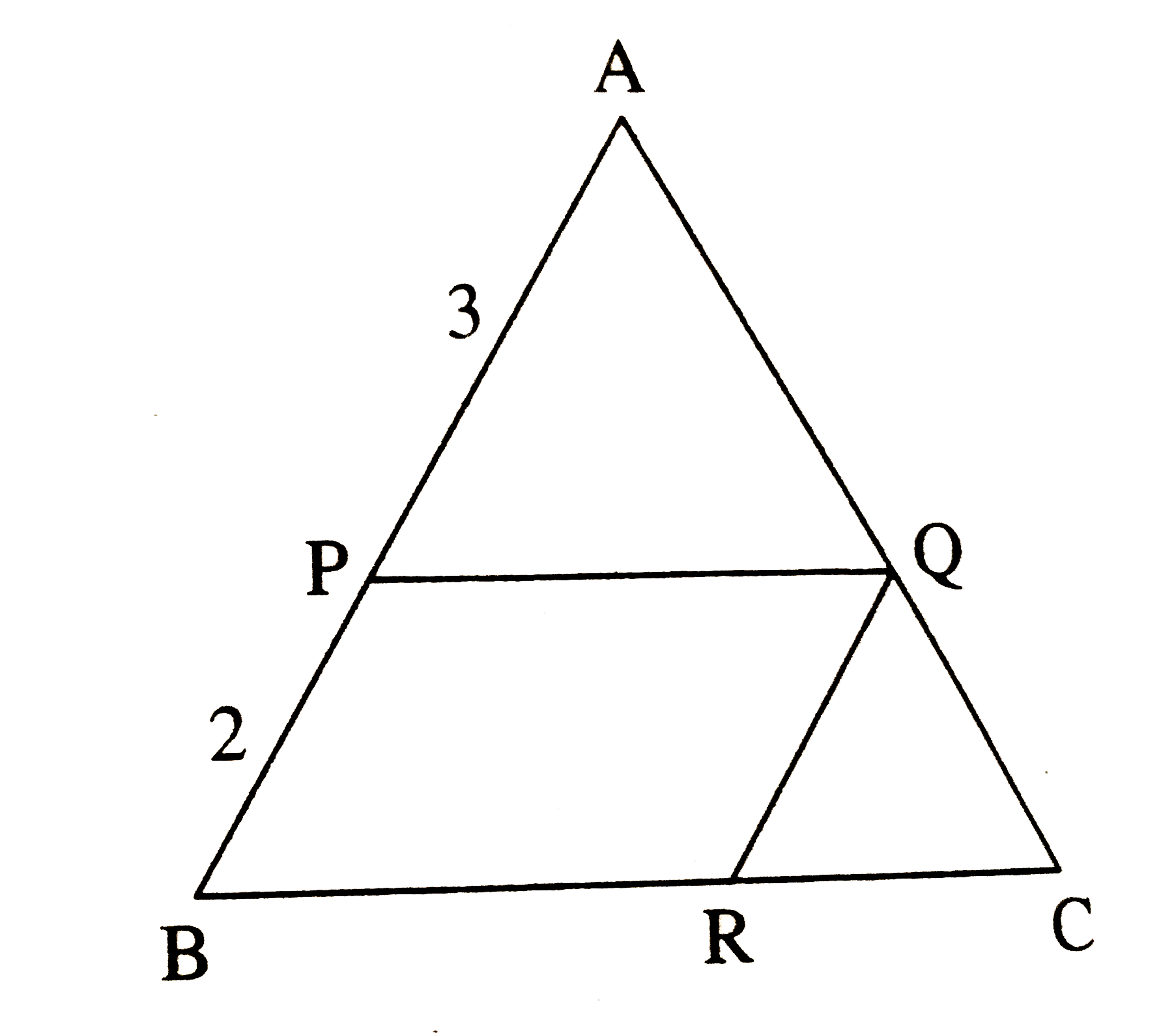
View SolutionIn the figure, segPQ∣∣ side BC and seg QR∣∣ side AB.
(i) Find AQQC.
(ii) What would be CRRB ?
(iii) Is BPPA=BRRC?
View SolutionIn the figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that : seg SQ ∣∣ seg RP.

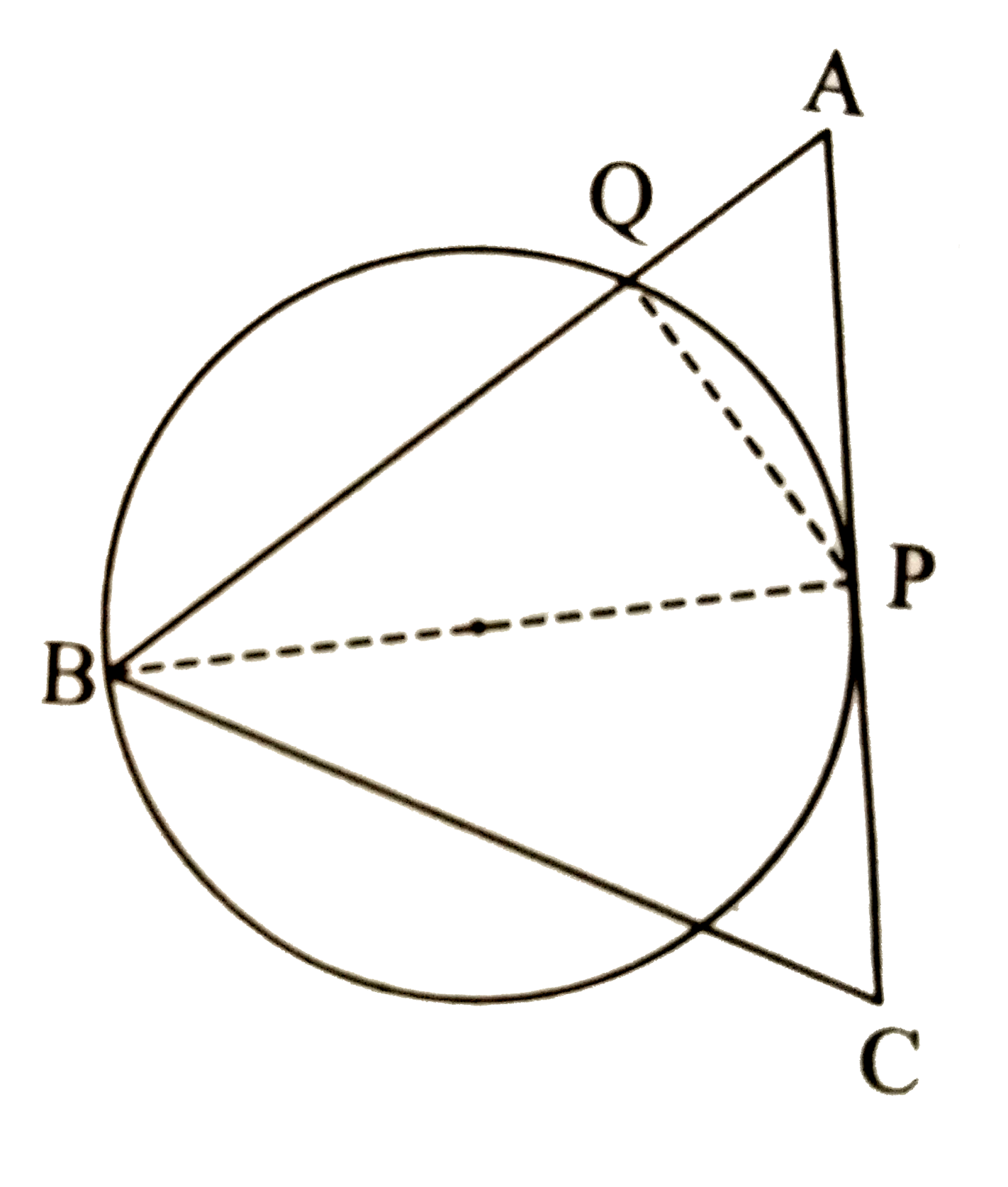
View SolutionIn ΔABC,AB=AC. A circle passing through B touches side AC at its midpoint P and intersects side AB at Q then prove BQ = 3AQ
Construction : Draw seg BP and seg PQ
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP⊥ line PQ and seg BQ⊥ line PQ.
Prove that, seg CP≅ seg CQ.

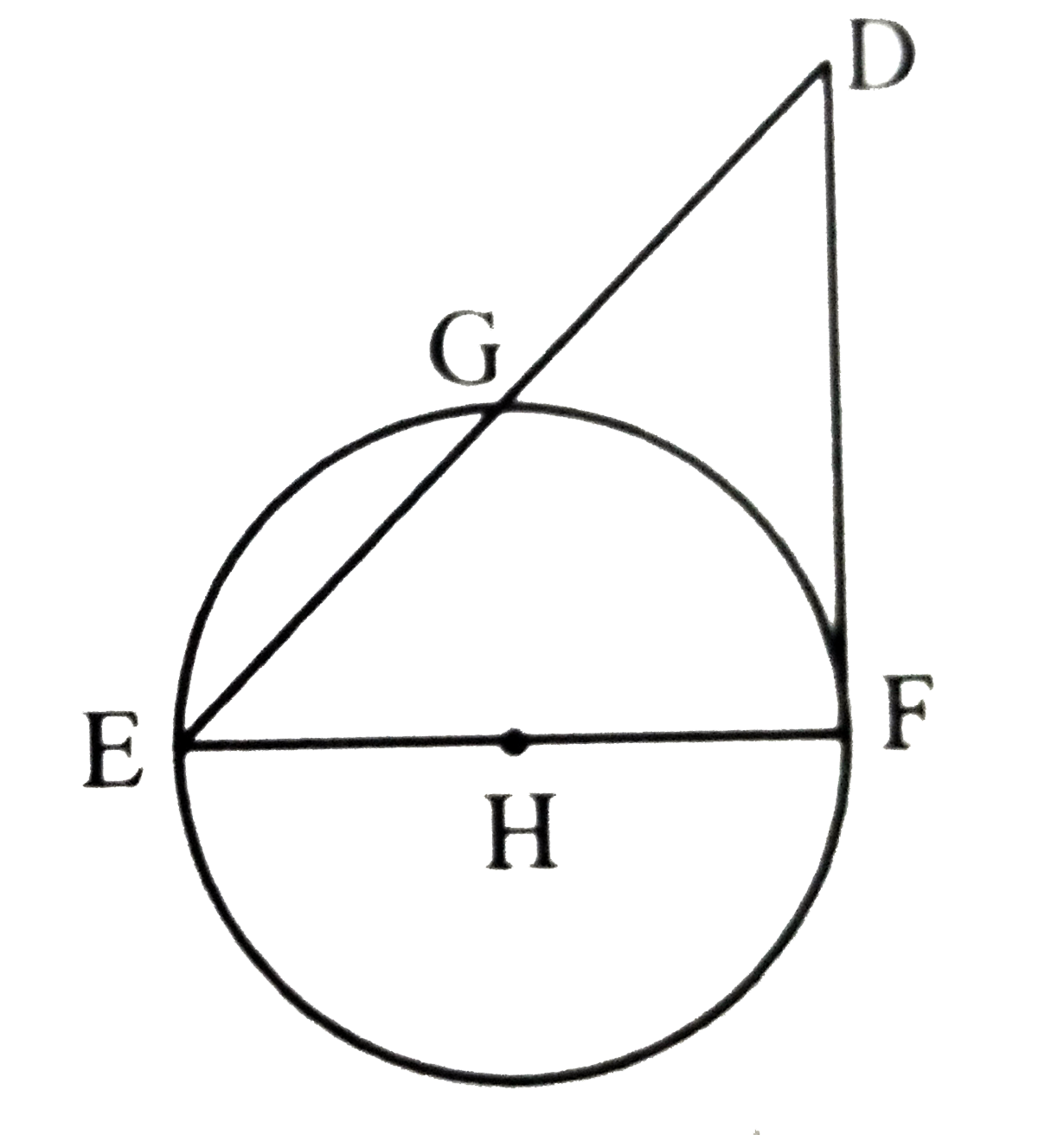
View SolutionIn the adjoining figure , seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE×GE=4r2.
View SolutionAs shown in the adjoining figure , two circles centred at A and B are touching at C. Line passing through C intersects the two circles at M and N respectively.
Show that seg AM ∣∣seg BN.
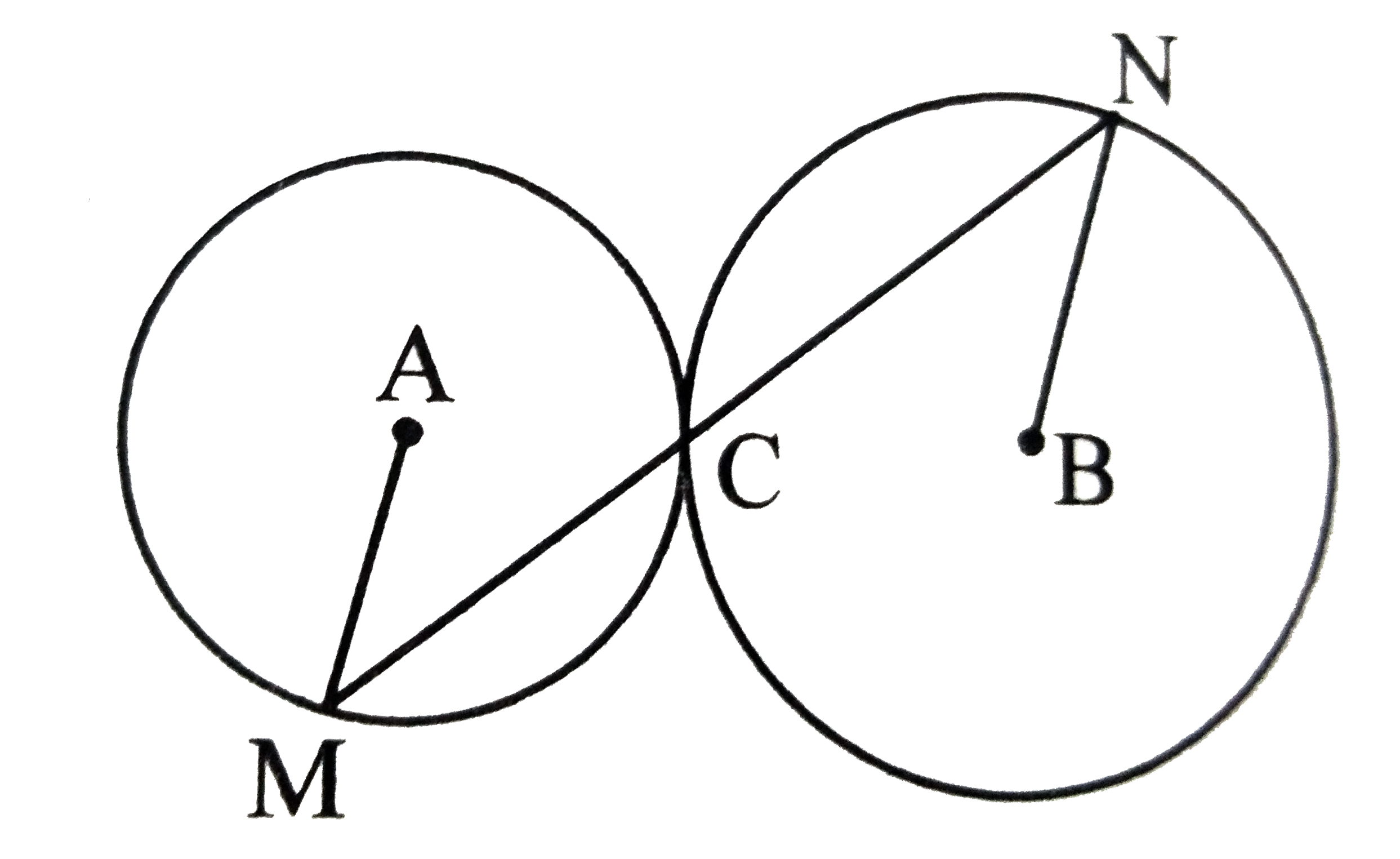
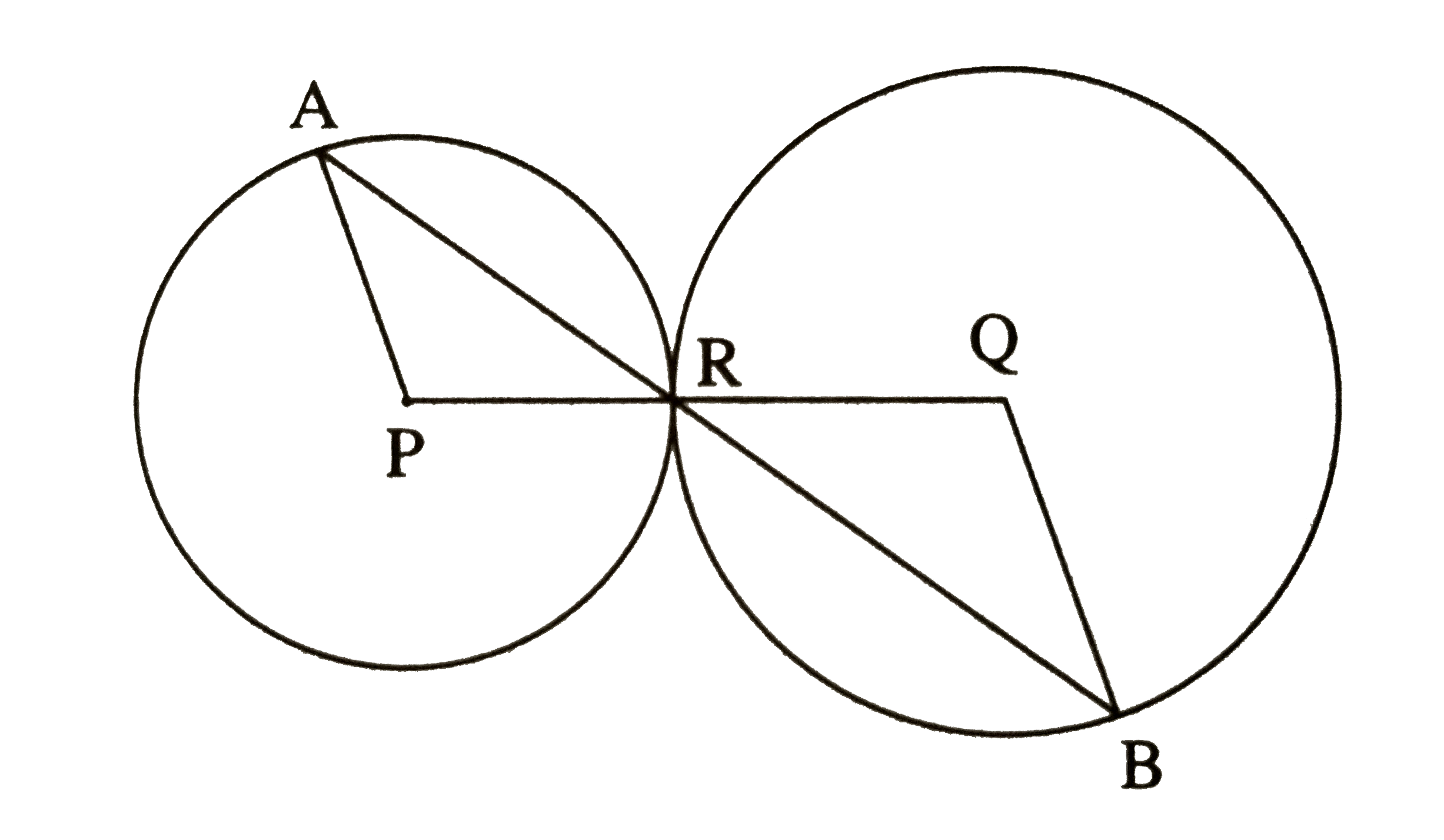
View SolutionIn the figure, the circles with centers P and Q touch each other at R.A line passing through R meets the circles at A and B respectively. Prove that
seg AP || seg BQ
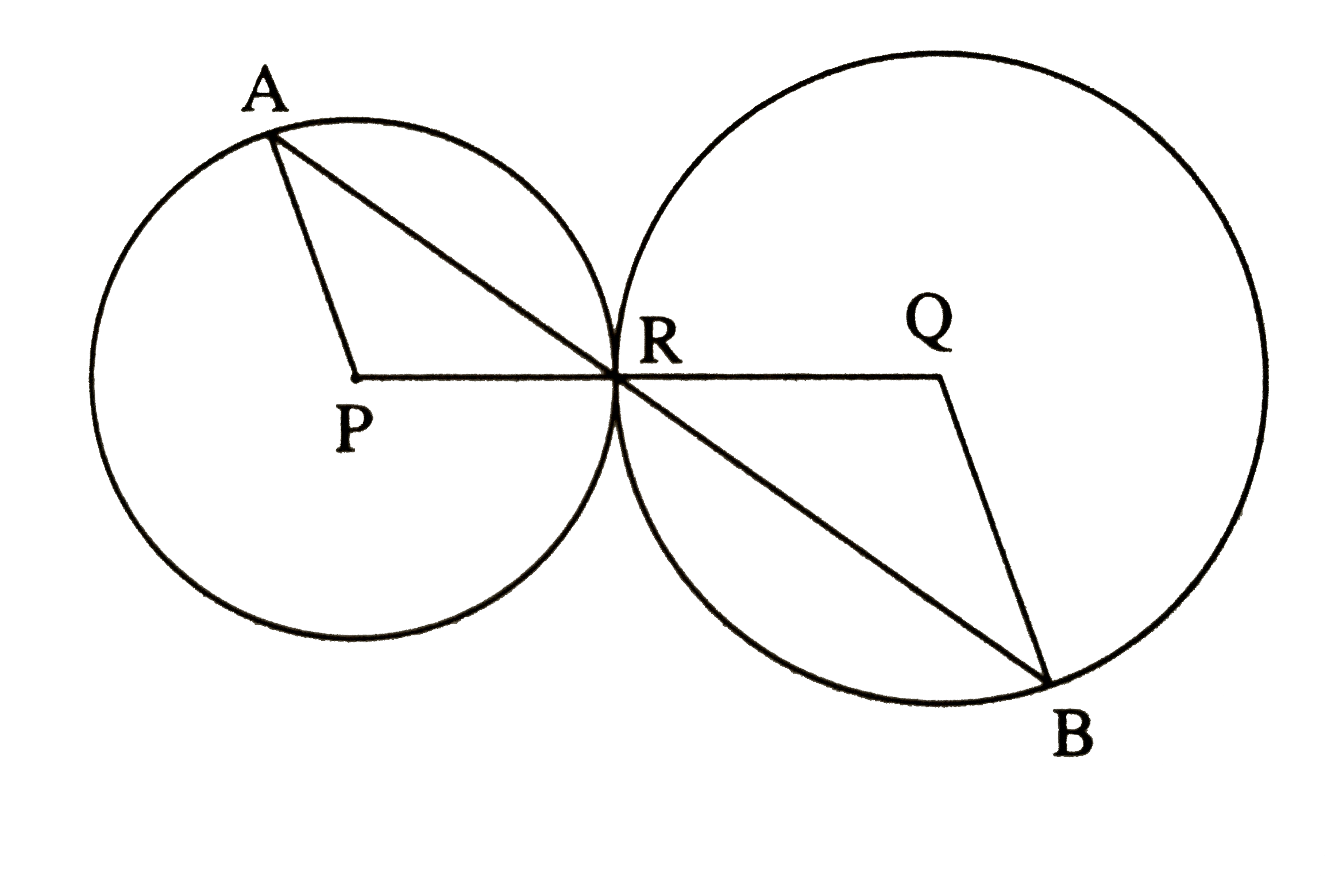
View SolutionIn the figure, the circles with centers P and Q touch each other at R.A line passing through R meets the circles at A and B respectively. Prove that
△APR~△RQB
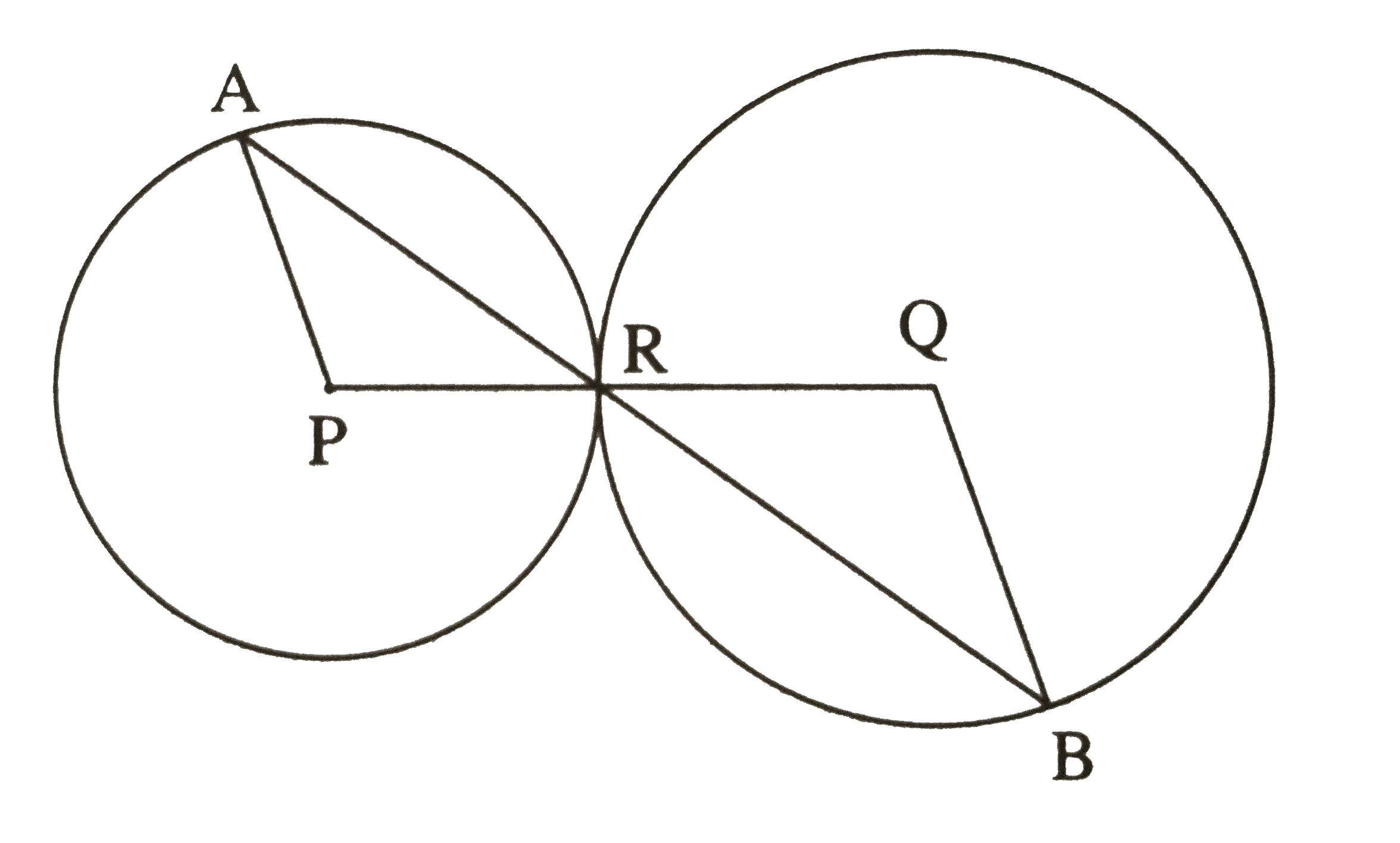
View SolutionIn the figure, the circles with centers P and Q touch each other at R.A line passing through R meets the circles at A and B respectively.
Find ∠RQB if ∠PAR=35∘
View SolutionIn the figure, the circles with centeres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD, if the radii of the circle are 4 cm, 6 cm.
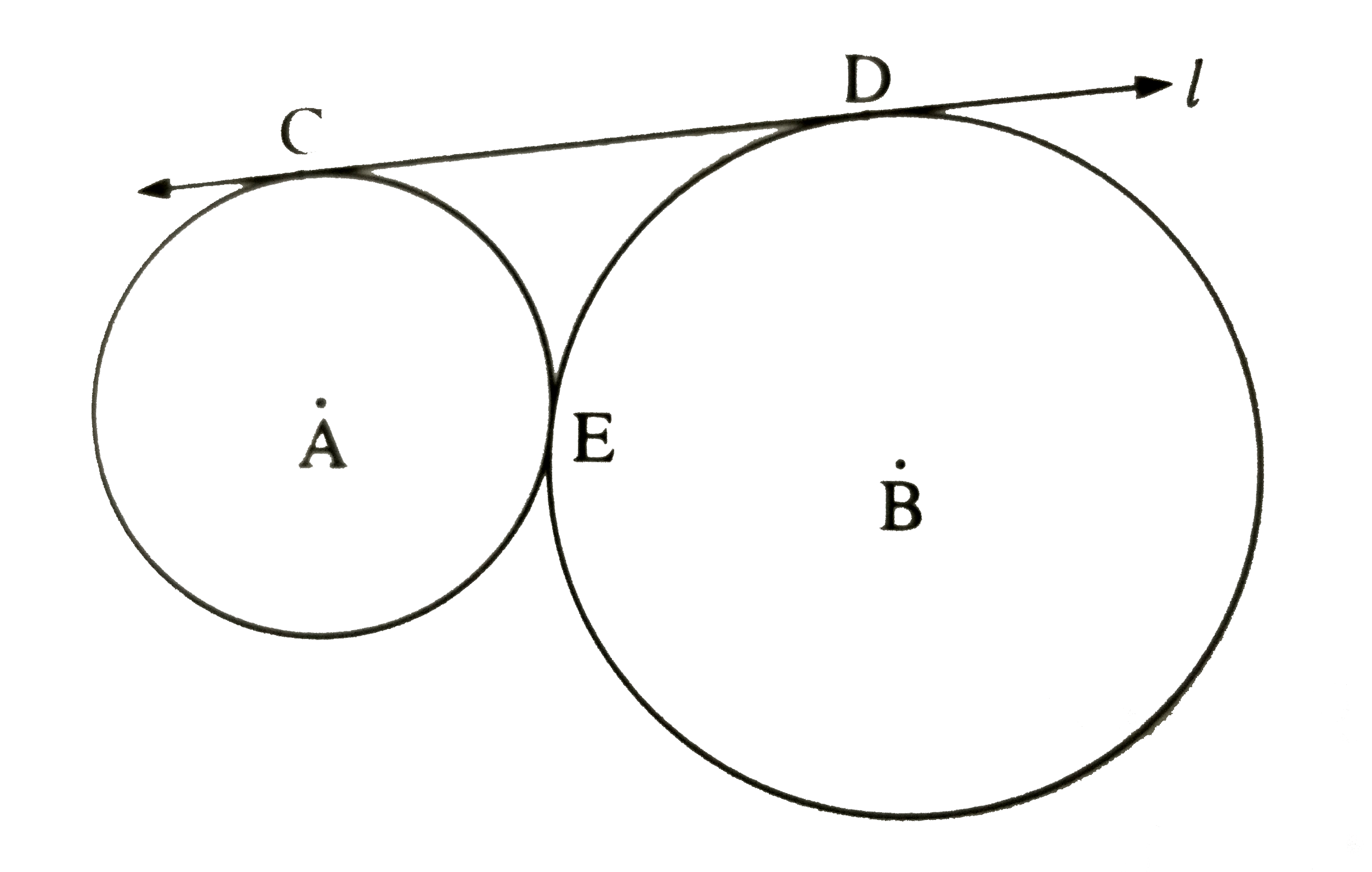
View Solution
