In the adjoining figure,AB is the diameter of the circle of centre O & the chord CD is equal to radius. If P is an external point, then find the value of ∠APB.
The correct Answer is:60∘
To find the value of angle APB in the given circle where AB is the diameter and CD is a chord equal to the radius, we can follow these steps:
Step 1: Understand the Given Information
- AB is the diameter of the circle.
- O is the center of the circle.
- CD is a chord equal to the radius R of the circle.
- P is an external point.
Step 2: Identify Key Properties
- The angle subtended by a chord at the center of the circle is twice the angle subtended at the circumference by the same chord.
- A diameter subtends a right angle to any point on the circumference.
Step 3: Draw the Diagram
- Draw the circle with center O, diameter AB, and chord CD.
- Mark point P outside the circle.
Step 4: Analyze Triangle OCD
Since CD=R (the radius), and OC=OD=R (the radii of the circle), triangle OCD is an equilateral triangle. Thus:
- ∠COD=60∘.
Step 5: Relate Angles Using Circle Properties
Using the property of angles subtended by a chord:
- ∠COD=2×∠CBD
- Therefore, 60∘=2×∠CBD
- This gives ∠CBD=30∘.
Step 6: Use the Diameter Property
Since AB is the diameter, it subtends a right angle at point D:
- ∠ADB=90∘.
Step 7: Find Angle PDB
Since ADB and PDB form a linear pair:
- ∠ADB+∠PDB=180∘
- Thus, 90∘+∠PDB=180∘
- This leads to ∠PDB=90∘.
Step 8: Analyze Triangle PDB
In triangle PDB:
- The sum of angles is 180∘:
- ∠PDB+∠DBP+∠DPB=180∘
- Substituting the known values: 90∘+30∘+∠APB=180∘.
Step 9: Solve for Angle APB
- Rearranging gives:
∠APB=180∘−(90∘+30∘)
∠APB=180∘−120∘
∠APB=60∘.
Final Answer
Thus, the value of ∠APB is 60∘.
---
- AB is the diameter of the circle.
- O is the center of the circle.
- CD is a chord equal to the radius R of the circle.
- P is an external point.
- The angle subtended by a chord at the center of the circle is twice the angle subtended at the circumference by the same chord.
- A diameter subtends a right angle to any point on the circumference.
- Draw the circle with center O, diameter AB, and chord CD.
- Mark point P outside the circle.
Since CD=R (the radius), and OC=OD=R (the radii of the circle), triangle OCD is an equilateral triangle. Thus:
- ∠COD=60∘.
Using the property of angles subtended by a chord:
- ∠COD=2×∠CBD
- Therefore, 60∘=2×∠CBD
- This gives ∠CBD=30∘.
Since AB is the diameter, it subtends a right angle at point D:
- ∠ADB=90∘.
Since ADB and PDB form a linear pair:
- ∠ADB+∠PDB=180∘
- Thus, 90∘+∠PDB=180∘
- This leads to ∠PDB=90∘.
In triangle PDB:
- The sum of angles is 180∘:
- ∠PDB+∠DBP+∠DPB=180∘
- Substituting the known values: 90∘+30∘+∠APB=180∘.
- Rearranging gives:
∠APB=180∘−(90∘+30∘)
∠APB=180∘−120∘
∠APB=60∘.
Thus, the value of ∠APB is 60∘.
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Revision Exercise (very Short Answer Question)
10 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Revision Exercise (short Answer Questions )
10 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
In the adjoining figure, O is the centre of the circle. If the chord AB is equal to the radius of the circle, then find the value of ∠ADB.

View SolutionIn the adjoining figure AB||CD, find x and y

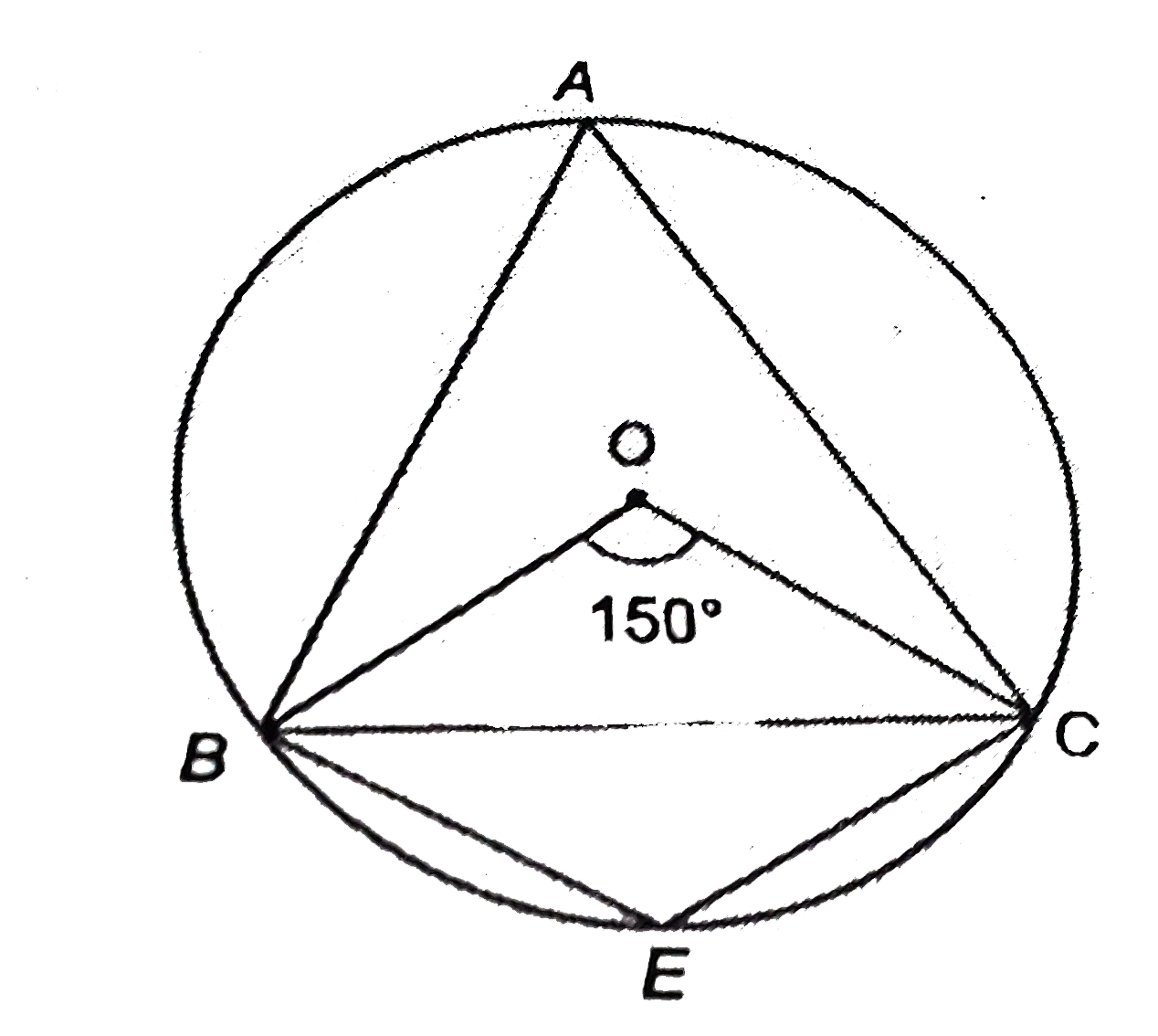
View SolutionIn the adjoining figure, O is the centre of the circle. Find the value of ∠BEC.
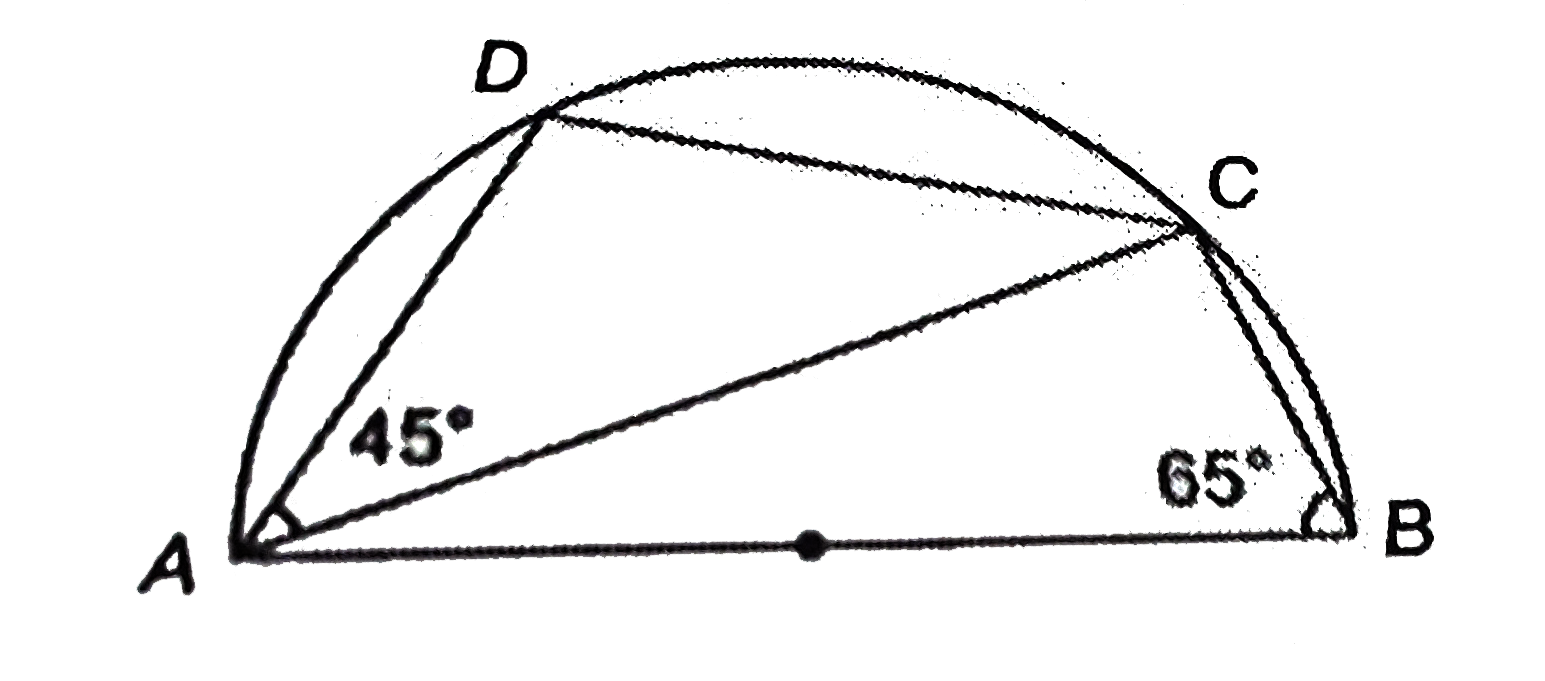
View SolutionIn the adjoining figure, AB is the diameter of the circle and two points C and D are on the circle. If ∠CAD=45∘ and ∠ABC=65∘, then find the value of ∠DCA.
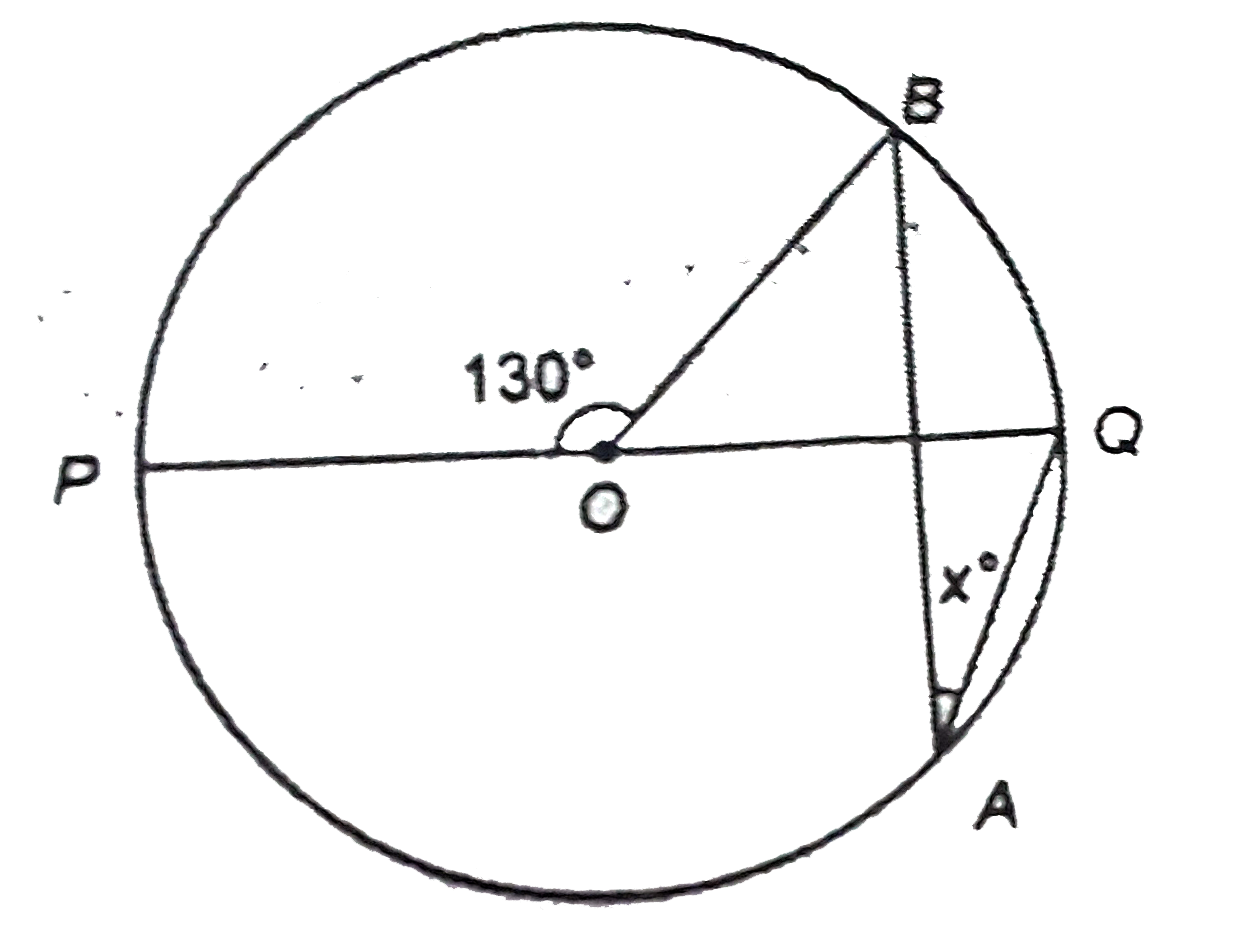
View SolutionIn the adjoining figure, O is the centre of the circle. If ∠BOP=130∘, then find the value of x.
View SolutionIn the adjoining figure, BD is the diameter of the circle which bisects the chord AC at point E. If AC=8cm, BE=2cm, then find the radius of the circle.

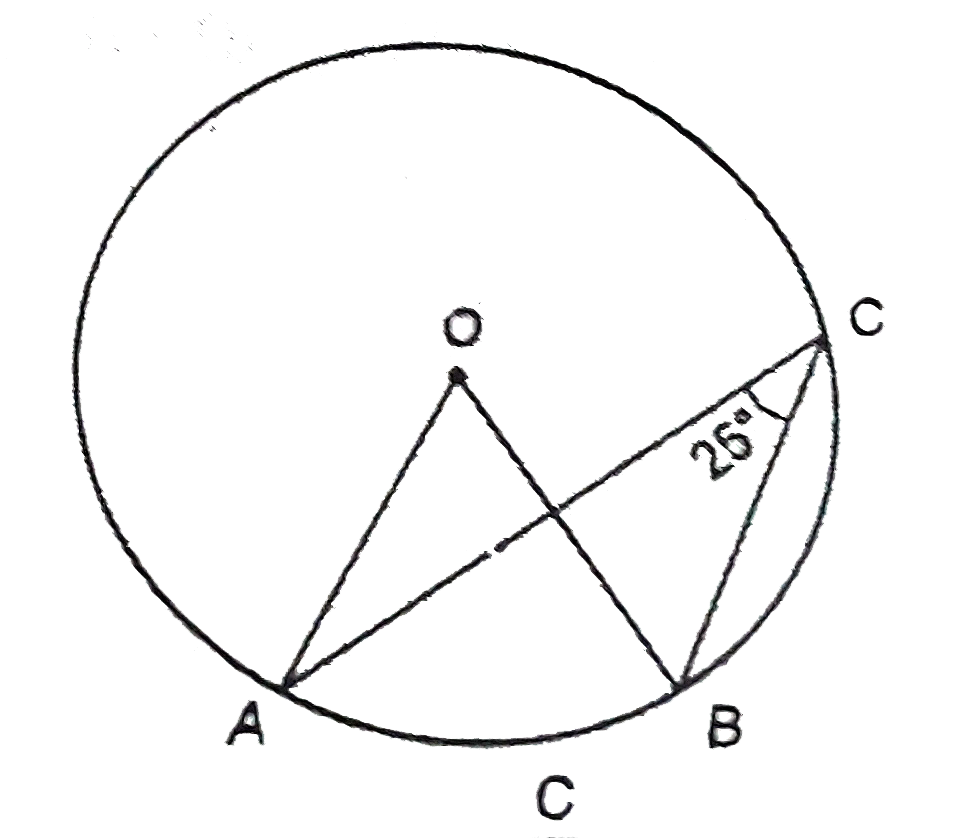
View SolutionIn the adjoining figure , O is the centre of the circle. If ∠ACB=25∘, then find ∠AOB.
View SolutionIn the adjoining figure, AD is the diameter of the circle and ∠BCD=140∘. Find the value of ∠ADB.

View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View SolutionIn the adjoining figure, O is the centre of the circle. If ∠AOB=70∘, then find the value of ∠OCD.

View Solution
