ABCD is a cyclic trapezium in which, AD| |BC and ∠B=70∘. Find its remaining angles,
The correct Answer is:∠A=110∘,angleC=70^@,∠D=110∘
To solve the problem, we will follow these steps:
Step 1: Understand the properties of a cyclic trapezium
In a cyclic trapezium, the sum of the opposite angles is equal to 180 degrees. This means:
- Angle A + Angle C = 180 degrees
- Angle B + Angle D = 180 degrees
Step 2: Use the given information
We are given that:
- Angle B = 70 degrees
Step 3: Find Angle D
Using the property of cyclic trapezium:
Angle D+Angle B=180∘
Substituting the value of Angle B:
Angle D+70∘=180∘
Now, solve for Angle D:
Angle D=180∘−70∘=110∘
Step 4: Find Angle A
Since AD is parallel to BC, we can use the property of co-interior angles:
Angle A+Angle B=180∘
Substituting the value of Angle B:
Angle A+70∘=180∘
Now, solve for Angle A:
Angle A=180∘−70∘=110∘
Step 5: Find Angle C
Using the property of cyclic trapezium again:
Angle A+Angle C=180∘
Substituting the value of Angle A:
110∘+Angle C=180∘
Now, solve for Angle C:
Angle C=180∘−110∘=70∘
Summary of Angles
- Angle A = 110 degrees
- Angle B = 70 degrees
- Angle C = 70 degrees
- Angle D = 110 degrees
Final Answer
The remaining angles are:
- Angle A = 110 degrees
- Angle C = 70 degrees
- Angle D = 110 degrees
---
In a cyclic trapezium, the sum of the opposite angles is equal to 180 degrees. This means:
- Angle A + Angle C = 180 degrees
- Angle B + Angle D = 180 degrees
We are given that:
- Angle B = 70 degrees
Using the property of cyclic trapezium:
Angle D+Angle B=180∘
Substituting the value of Angle B:
Angle D+70∘=180∘
Now, solve for Angle D:
Angle D=180∘−70∘=110∘
Since AD is parallel to BC, we can use the property of co-interior angles:
Angle A+Angle B=180∘
Substituting the value of Angle B:
Angle A+70∘=180∘
Now, solve for Angle A:
Angle A=180∘−70∘=110∘
Using the property of cyclic trapezium again:
Angle A+Angle C=180∘
Substituting the value of Angle A:
110∘+Angle C=180∘
Now, solve for Angle C:
Angle C=180∘−110∘=70∘
- Angle A = 110 degrees
- Angle B = 70 degrees
- Angle C = 70 degrees
- Angle D = 110 degrees
The remaining angles are:
- Angle A = 110 degrees
- Angle C = 70 degrees
- Angle D = 110 degrees
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Revision Exercise (very Short Answer Question)10videos
CIRCLE
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Revision Exercise (short Answer Questions )10videos
CIRCLE
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10b19videos
CIRCLE
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)5videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise8videos
CO-ORDINATE GEOMETRY
Similar Questions
ABCD is a cyclic trapezium m, in which AB∣∣DC. If ∠B=75∘ , then find other angles.
View SolutionABCD is a trapezium in which AB∣∣DCand∠A=∠B=45∘. Find angles C and D of the trapezium.
View SolutionABCD is a cyclic trapezium with AD∣∣BC. If ∠B=700, determine other three angles of the trapezium.
View SolutionIn a cyclic quadrilateral ABCD, if AB || CD and ∠B=700, find the remaining angles.
View SolutionABCD is a cyclic quadrilateral in which BC is paralleld to AD, angle ADC=110∘ and angle BAC=50∘. Find angle DAC and angle DCA.
View SolutionAn angle of a cyclic trapezium is twice the other angle. Find the value of the smaller angle.
View SolutionABCD is a trapezium in which AB||DC and P,Q are points on AD and BC respectively, such that PQ||DC, if PD=18 cm, BQ=35 cm and QC=15 cm. Find AD.
View SolutionIn the following figure , ABCD is a cyclic quadrilateral in which AD is parallel to BC .
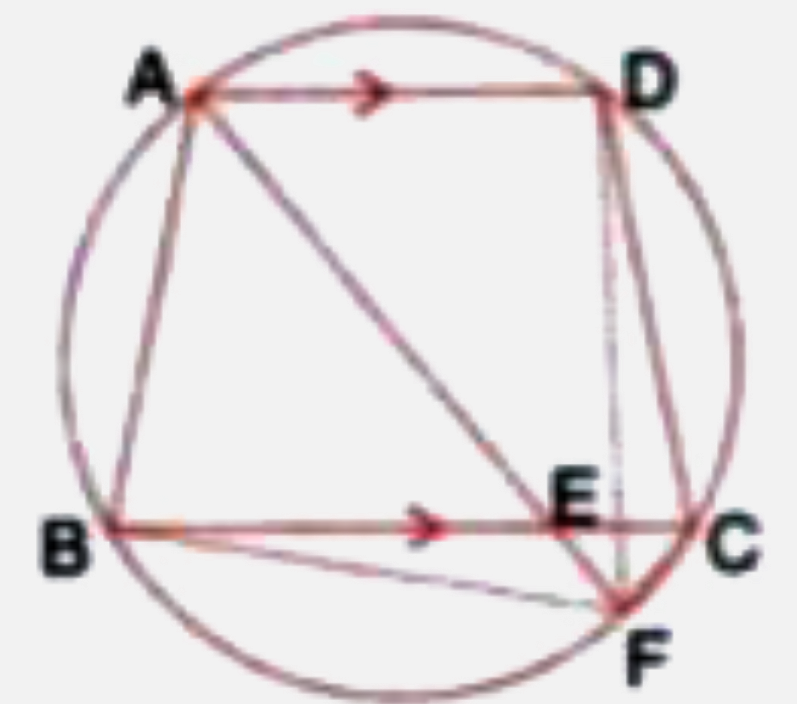
If the bisector of angle A meets BC at point E and given circle at point F, prove that :
(i) EF =FC
(ii) BF = DFView SolutionIn the given figures ABCD is a trapezium with DC //AB , ∠AOB=126∘and∠DCQ=∠CDP=52∘
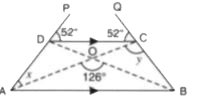 View Solution
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
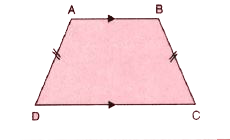
∠A=∠BView Solution

