in the figure above, ABCD is a square. M is the point one-third of the way from B to C. N is the point one-half of the way from D to C. Then θ=
50.8∘
45.0∘
36.9∘
36.1∘
The correct Answer is:B
To solve the problem step-by-step, we will analyze the square ABCD and the points M and N as described in the question.
Step 1: Define the square and points
Let the side length of square ABCD be x. The coordinates of the points can be defined as follows:
- A(0,0)
- B(0,x)
- C(x,x)
- D(x,0)
Step 2: Determine the coordinates of points M and N
- Point M is one-third of the way from B to C. Therefore, the coordinates of M can be calculated as:
M=B+13(C−B)=(0,x)+13((x,x)−(0,x))=(0,x)+13(x,0)=(x3,x)
- Point N is one-half of the way from D to C. Therefore, the coordinates of N can be calculated as:
N=D+12(C−D)=(x,0)+12((x,x)−(x,0))=(x,0)+12(0,x)=(x,x2)
Step 3: Calculate angles BAM and DAN
- For angle BAM:
- The length BM=x3 (vertical distance from B to M).
- The length AB=x (horizontal distance from A to B).
The tangent of angle BAM is given by:
tan(∠BAM)=BMAB=x3x=13
Therefore, ∠BAM=tan−1(13).
- For angle DAN:
- The length DN=x2 (vertical distance from D to N).
- The length AD=x (horizontal distance from A to D).
The tangent of angle DAN is given by:
tan(∠DAN)=DNAD=x2x=12
Therefore, ∠DAN=tan−1(12).
Step 4: Use the angles to find theta
Since angle DAB is a right angle (90 degrees), we can express it as:
∠DAB=∠DAN+θ+∠BAM
Substituting the known values:
90∘=tan−1(12)+θ+tan−1(13)
Step 5: Calculate the angles
Using approximate values:
- tan−1(13)≈18.4∘
- tan−1(12)≈26.6∘
Substituting these values into the equation:
90∘=26.6∘+θ+18.4∘
90∘=45∘+θ
θ=90∘−45∘=45∘
Final Answer
Thus, the value of θ is 45∘.
Let the side length of square ABCD be x. The coordinates of the points can be defined as follows:
- A(0,0)
- B(0,x)
- C(x,x)
- D(x,0)
- Point M is one-third of the way from B to C. Therefore, the coordinates of M can be calculated as:
M=B+13(C−B)=(0,x)+13((x,x)−(0,x))=(0,x)+13(x,0)=(x3,x)
N=D+12(C−D)=(x,0)+12((x,x)−(x,0))=(x,0)+12(0,x)=(x,x2)
- For angle BAM:
- The length BM=x3 (vertical distance from B to M).
- The length AB=x (horizontal distance from A to B).
The tangent of angle BAM is given by:
tan(∠BAM)=BMAB=x3x=13
Therefore, ∠BAM=tan−1(13).
- The length DN=x2 (vertical distance from D to N).
- The length AD=x (horizontal distance from A to D).
The tangent of angle DAN is given by:
tan(∠DAN)=DNAD=x2x=12
Therefore, ∠DAN=tan−1(12).
Since angle DAB is a right angle (90 degrees), we can express it as:
∠DAB=∠DAN+θ+∠BAM
Substituting the known values:
90∘=tan−1(12)+θ+tan−1(13)
Using approximate values:
- tan−1(13)≈18.4∘
- tan−1(12)≈26.6∘
90∘=26.6∘+θ+18.4∘
90∘=45∘+θ
θ=90∘−45∘=45∘
Thus, the value of θ is 45∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
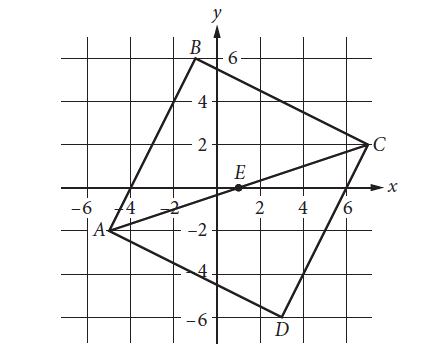
In the xy-plane above, ABCD is a square and point E is the center of the square. The coordinates of points C and E are (7, 2) and (1, 0), respectively. Which of the following is an equation of the line that passes through points B and D ?Ay=−3x−1By=−3(x−1)Cy=−13x+4Dy=−13x−1
In Figure, if AB∣∣DC and P is the mid-point BD, prove that P is also the midpoint of AC
View SolutionIn Figure, AC>AB and D is the point on AC such that AB=AD. Prove that BC>CD
View SolutionLook at the figure and answer the question.
How does the heat get transferred from A B C D point A to the hand?

View SolutionThe area of square ABCD is 16 cm2. Find the area of the square joining the mid-point of the sides.
View SolutionA (-2,4) , C (4,10) and D (-2,10) are the vertices of a square ABCD. Use the graphical method to find ordinates of the fourth vertex B. Also, find:
The co ordinates of the point of intersection of the diagonals of the square ABCD.
View SolutionIn right triangle ABC , right angle at C, M is the mid-point of the hypotenuse AB. C is jointed to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that AMC≅BMD (ii) ∠DBC=∠ACB DBC≅ACB (iii) CM=12AB
View SolutionDivide Rs1,870 into three parts in such a way that half of the first part, one-third of the second part and one-sixth of the third part are all equal.
View Solution
