In the figure, circle with centre M touches the circle with centre N at point T. Radius RM touches the smaller circle at S. Radii of circles are 9 cm and 2.5 cm. Find the answers to the following questions hence find the ratio MS: SR
(1) Find the length of segment MT
(2) Find the length of seg MN
(3) Find the measure of ∠NSM.

The correct Answer is:(i) MT=9cm (ii) ∴ MN=6.5cm (iii) ∴∠NSM=90∘
Step by step video & image solution for In the figure, circle with centre M touches the circle with centre N at point T. Radius RM touches the smaller circle at S. Radii of circles are 9 cm and 2.5 cm. Find the answers to the following questions hence find the ratio MS: SR (1) Find the length of segment MT (2) Find the length of seg MN (3) Find the measure of /_ NSM . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Activities for Practice
4 Videos
- CIRCLEBOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Multiple Choice Question
25 Videos
- CIRCLEBOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Practice Set 3.5
5 Videos
- CHALLENGING QUESTIONS BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Chapter 6: Statistics
4 Videos
- CO-ORDINATE GEOMETRYBOOK - TARGET PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - CHAPTER ASSESSMENT
19 Videos
Similar Questions
In the figure, A is the centre of the circle. AN = 10 cm . Line MN touches the circles in point M. If MN = 6 cm then find the radius of the circle.
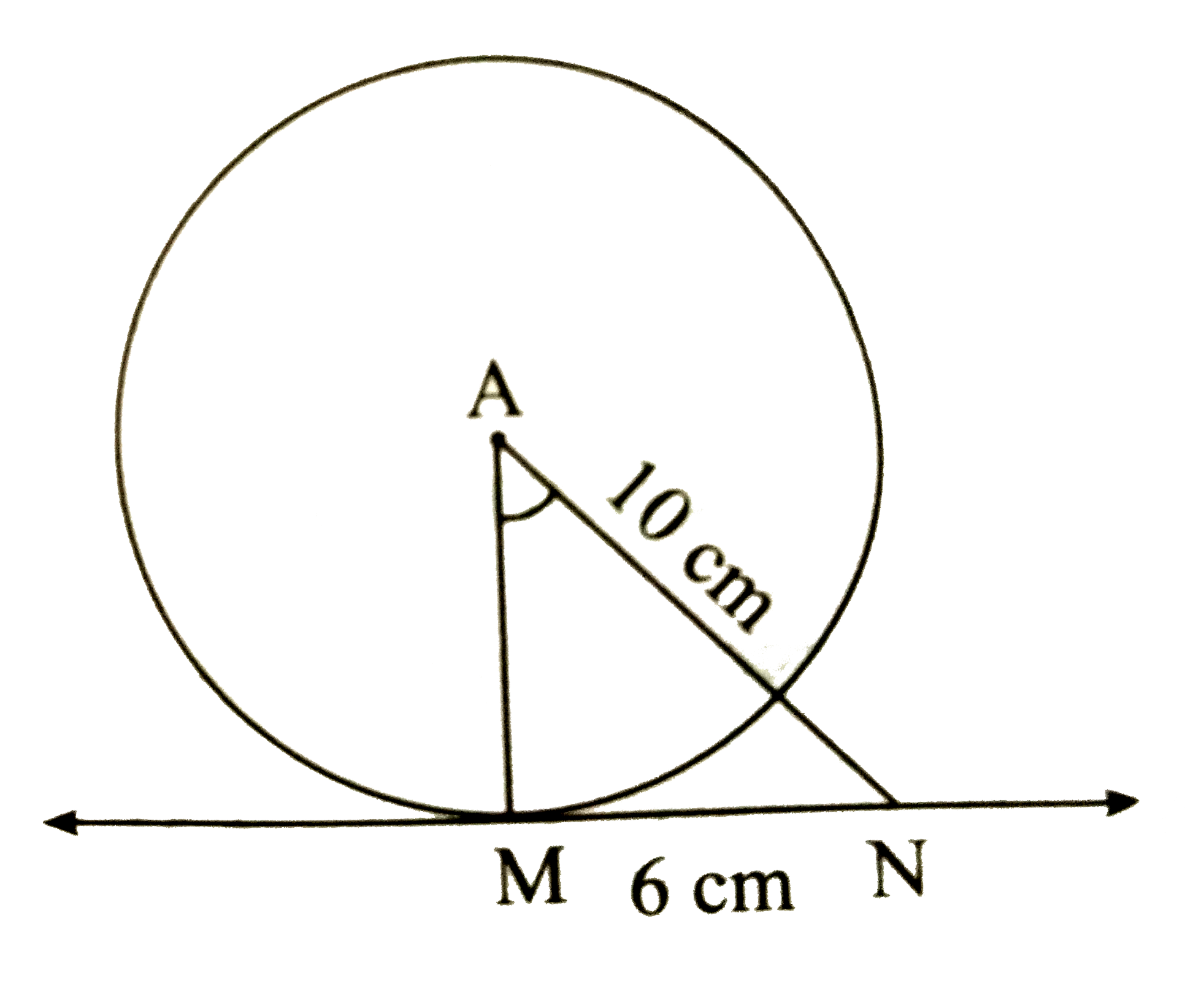
View SolutionO is the centre of the smaller circle, O' is the centre of bigger circle.CD is tangent to the smaller circle,Find the radius of the smaller circle.
View Solution
Knowledge Check
In the figure, point P is the centre of the circle and line AB is the tangent to the circle at the point T. The radius of the circle is 6 cm . Find PB, if ∠TPB=60∘
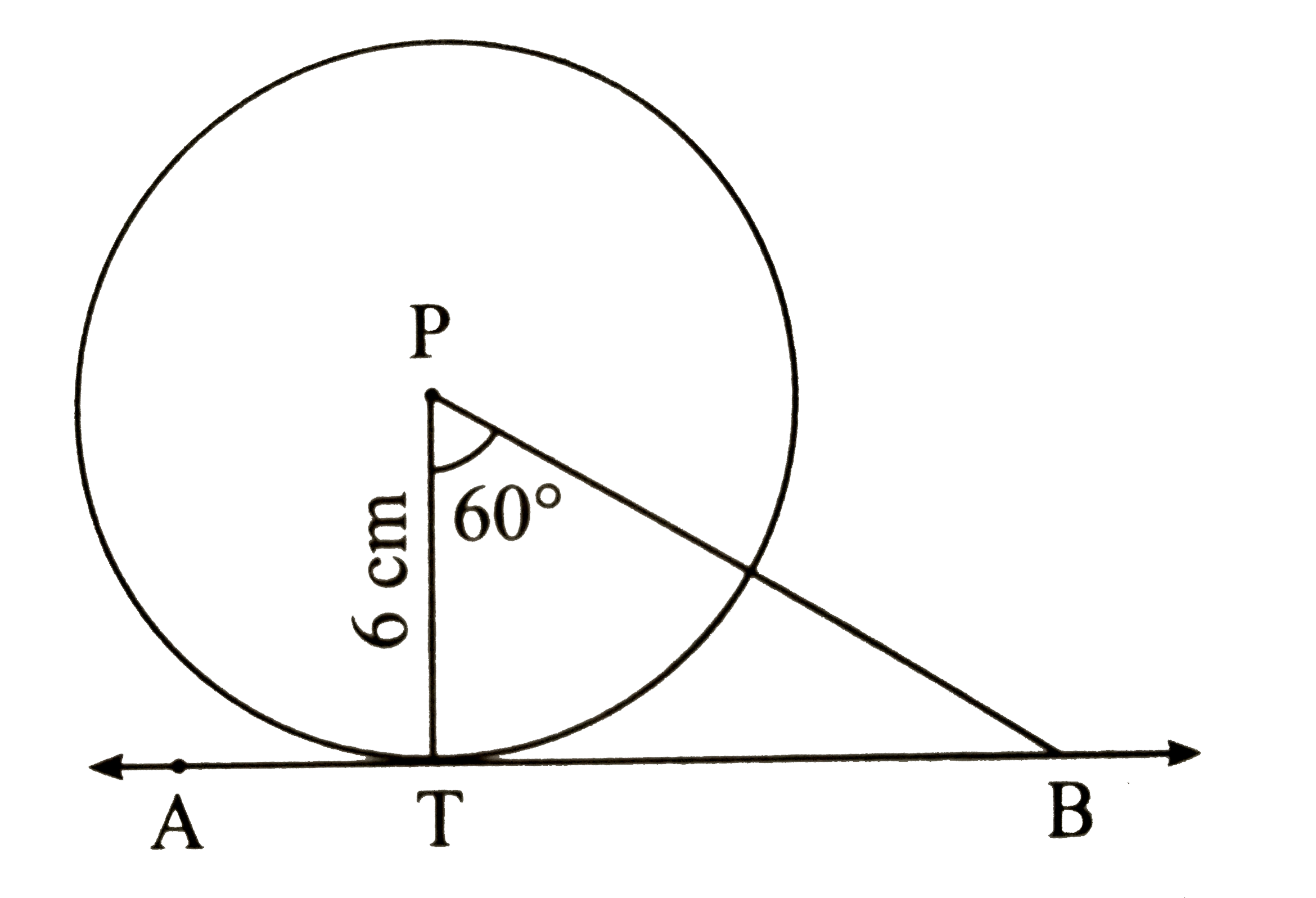 A5√5cmB10√5cmC(10−5√3)cmD(10−5√3)cm
A5√5cmB10√5cmC(10−5√3)cmD(10−5√3)cmThe length of a chord of a circle of radius 10 cm is 12 cm. Find the distance of the chord from the centre of the circle.
A6 cmB5 cmC8 cmD7 cm
In the figure, point P is the centre of the circle and line AB is the tangent to the circle at the point T. The radius of the circle is 6 cm . Find PB, if ∠TPB=60∘

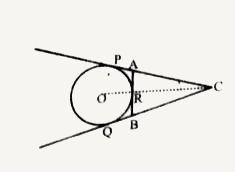
View SolutionIn figure, CP and CQ are tangents from an external point C to a circle with centre O. AB is another tangent which touches the circle at R. If CP = 11 cm and BR = 4 cm. Find the length of BC.
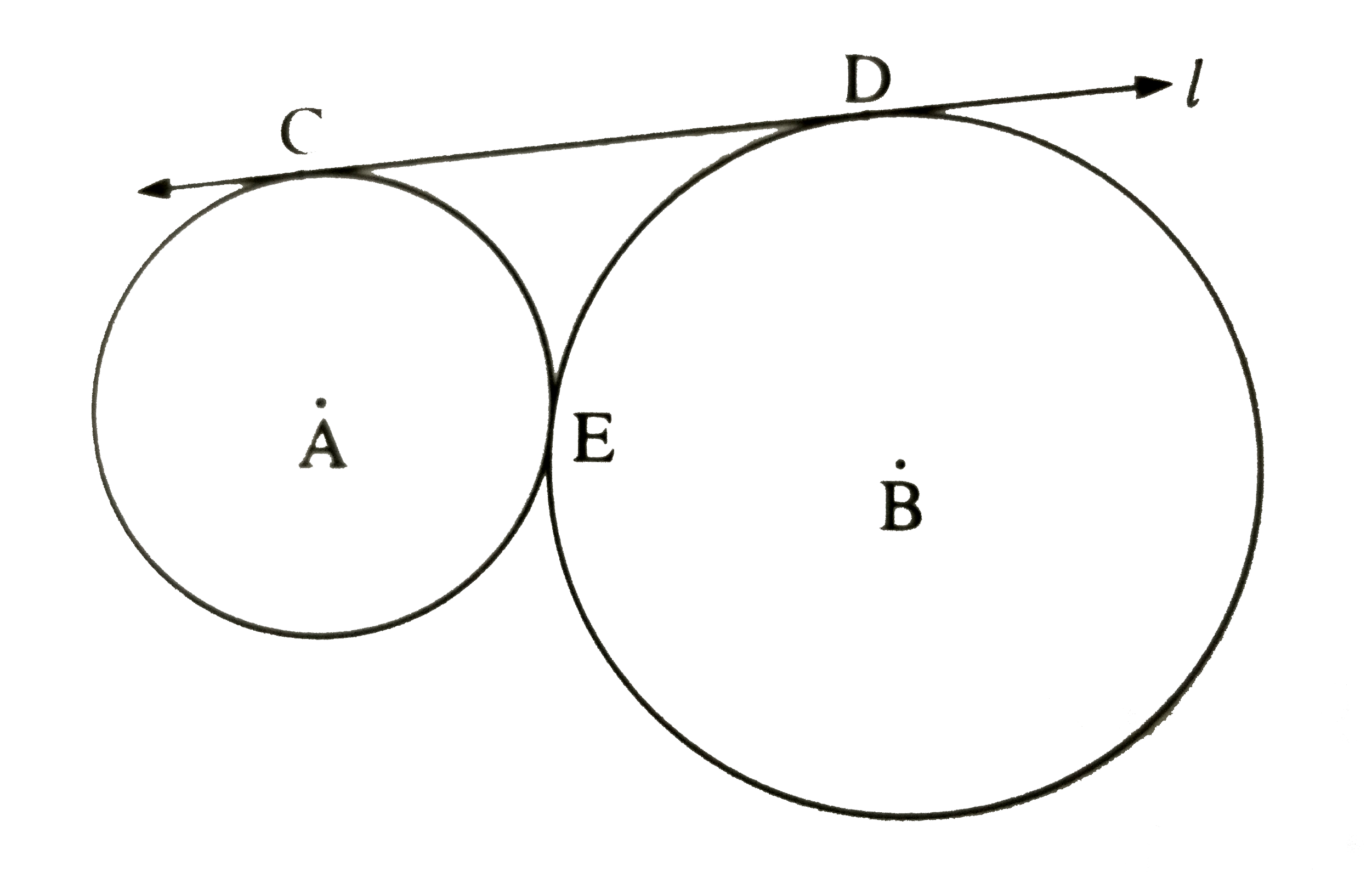
View SolutionIn the figure, the circles with centeres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD, if the radii of the circle are 4 cm, 6 cm.
View SolutionIn the given figure two small circles touch each other externally at the centre of a big circle and these small circles are touched internally by a big circle of radius 74cm. Find the area of the shaded region

View SolutionTwo circles of radii 5 cm and 3cm intersect at two points and the distance between their centres is 4cm. Find the length of the common chord.
Let the common chord be AB and Pand Q be the centers of the two circles.
AP=5cmand AQ=3cm.
PQ=4cm ...given
Now, segPQ⊥chordAB
AR=RB=12AB....perpendicular from center to the chord, bisects the chord
Let PR=xcm
so RQ=(4−x)cm
In△ARP,AP2=AR2+PR2
AR2=52−x2...(1)
In △ARQ,AQ2=AR2+QR2
AR2=32−(4−x)2...(2)
52−x2=32−(4−x)2...from (1) & (2)
25−x2=9−(16−8x+x2)
25−x2=−7+8x−x2
32=8x
x=4 substituting in equation(1) we get , AR2=25−16=9
AR=3cm
AB=2×AR=2×3=6
AB=6cmSo length of common chord is6 cm.
View SolutionIn two concentric circles, a chord of length 8cm of the larger circle touches the smaller circle. If the radius of the larger circle is 5cm then find the radius of the smaller circle.
View Solution
