In the adjoining figure, O is the centre of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB)=r. Prove that , □ ABOC is a square.
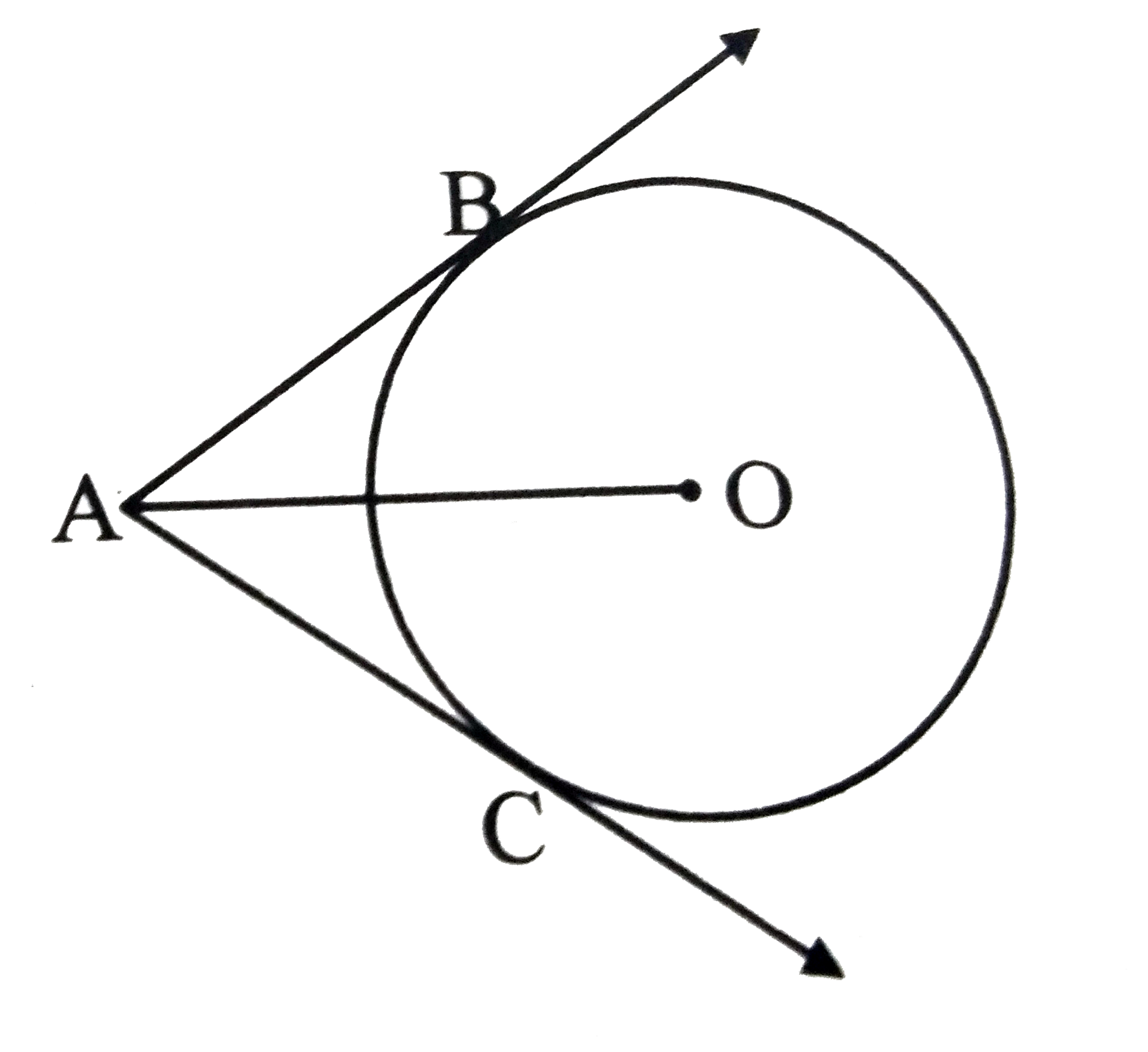
The correct Answer is:∴□ ABOC is a square .
Step by step video & image solution for In the adjoining figure, O is the centre of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB)=r. Prove that , square ABOC is a square. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBook:TARGET PUBLICATIONChapter:CIRCLEExercise:Activities for Practice
Explore 4 Videos
- CIRCLEBook:TARGET PUBLICATIONChapter:CIRCLEExercise:Multiple Choice Question
Explore 25 Videos
- CIRCLEBook:TARGET PUBLICATIONChapter:CIRCLEExercise:Practice Set 3.5
Explore 5 Videos
- CHALLENGING QUESTIONS Book:TARGET PUBLICATIONChapter:CHALLENGING QUESTIONS Exercise:Chapter 6: Statistics
Explore 4 Videos
- CO-ORDINATE GEOMETRYBook:TARGET PUBLICATIONChapter:CO-ORDINATE GEOMETRYExercise:CHAPTER ASSESSMENT
Explore 19 Videos
Similar Questions
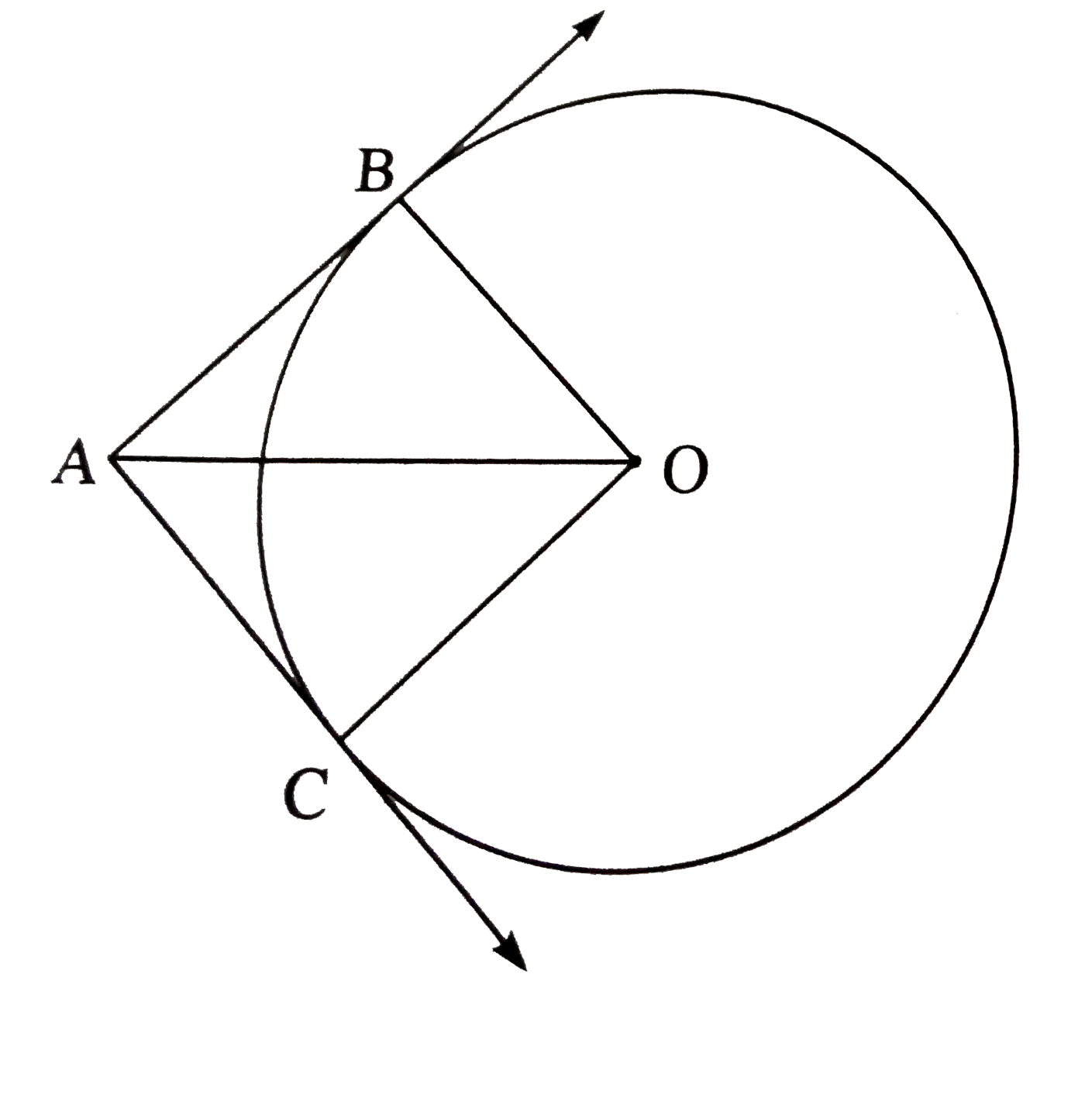
In the figure, O is the centre of the circle of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB)=r. Prove that, □ABOC is a square.
View SolutionIn the adjoining figure, O is the centre of the circle. AB is an arc of the circle and ∠AOB=80∘. Find ∠ACB.

View Solution
Knowledge Check
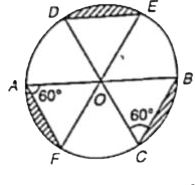
In the adjoining figure O is the centre of the circle with radius r’ AB, CD and EF are the diameters of the circle. angleOAF = angleOCB = 60^(@) . What is the area of the shaded region?
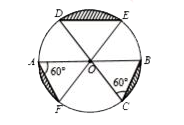 Ar22(π−3√32)Br22(π−3√34)Cr23(π−2√33)DData insuffincient
Ar22(π−3√32)Br22(π−3√34)Cr23(π−2√33)DData insuffincientIn the adjoining figure O is the centre of the circle. ∠AOD=120?∘. If the radius of the circle be 'r', then find the sum of the areas of quadrilaterals AODPandOBQC :
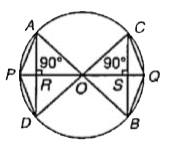 A√32r2B3√3r2C√3r2Dnone of these
A√32r2B3√3r2C√3r2Dnone of these
In the adjoining figure, O is the centre of the circle. If the chord AB is equal to the radius of the circle, then find the value of ∠ADB.

View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.

View SolutionIn the adjoining figure , seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE×GE=4r2.
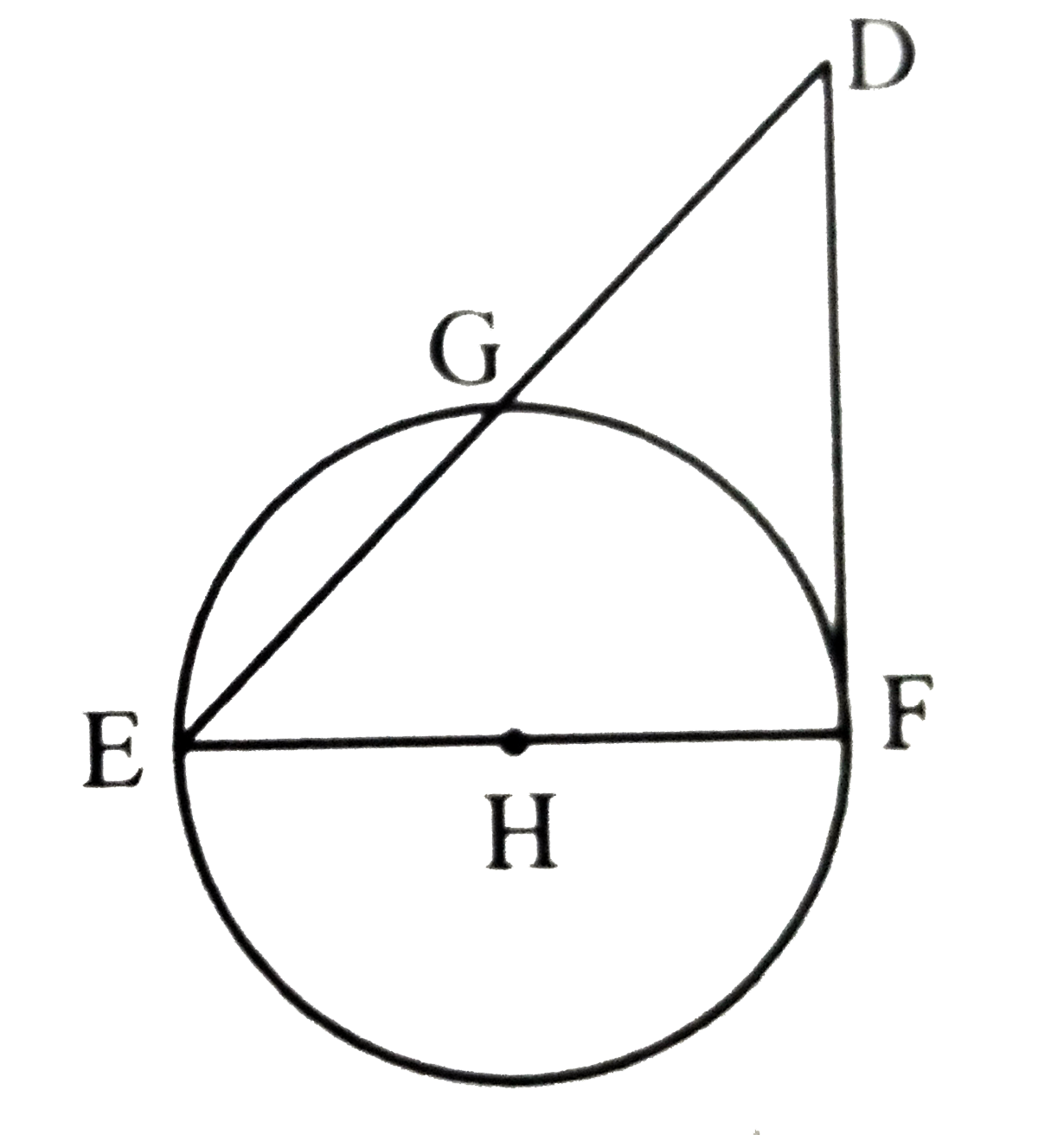
View SolutionIn the given figure O is the centre of the circle and AB is a tangent at B. If AB=15 cm and AC=7.5 cm, find the rdius of the circle.

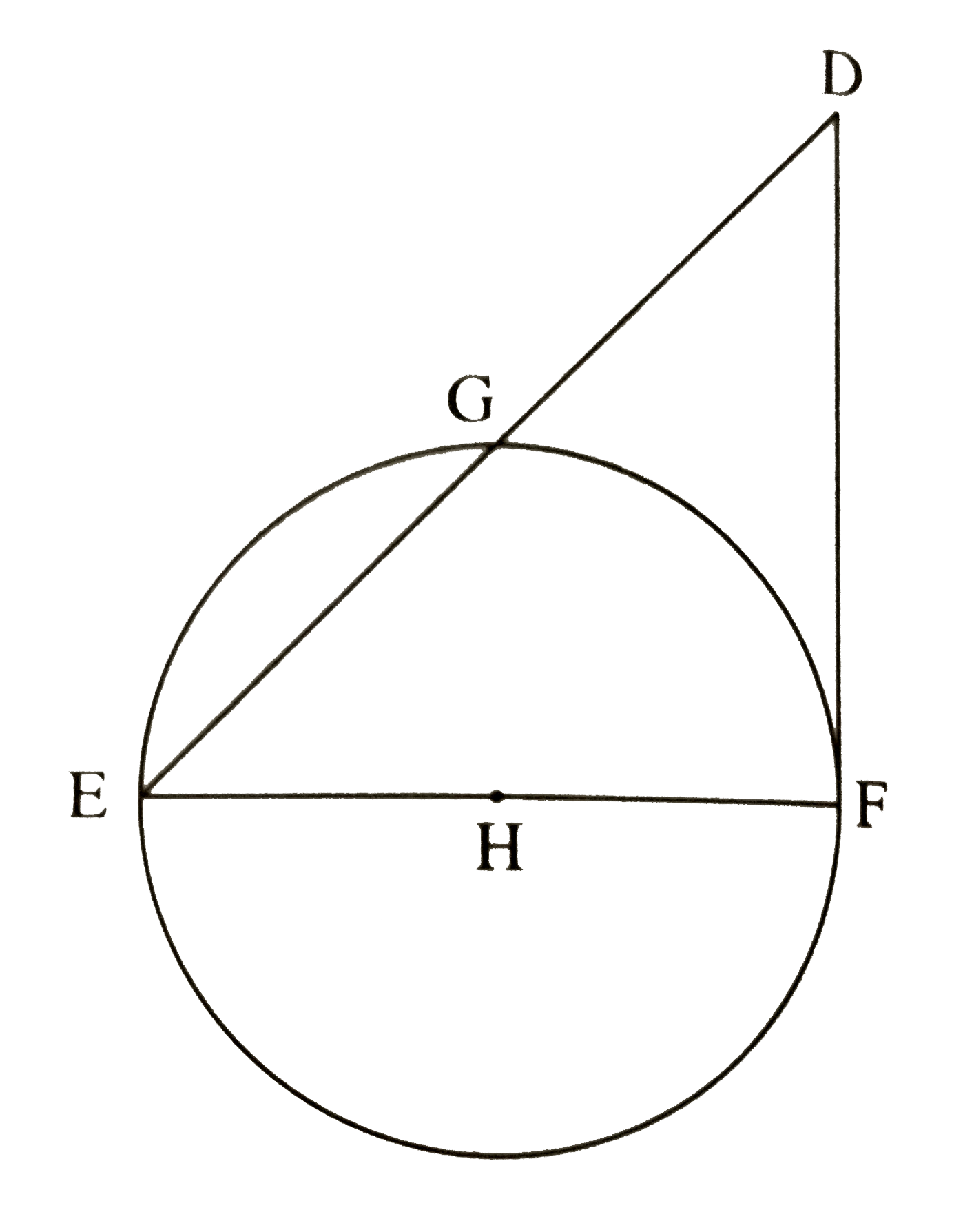
View SolutionIn figure, seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE×GE=4r2.
View SolutionIn the adjoining figure O is the centre of the circle with radius 'r' AB, CD and EF are the diameters of the circle. ∠OAF=∠OCB=60∘. What is the area of the shaded region?
View Solution