In the figure given below, P andQ are centres of two circles, intersecting at B and C , and ACD is a straight line.
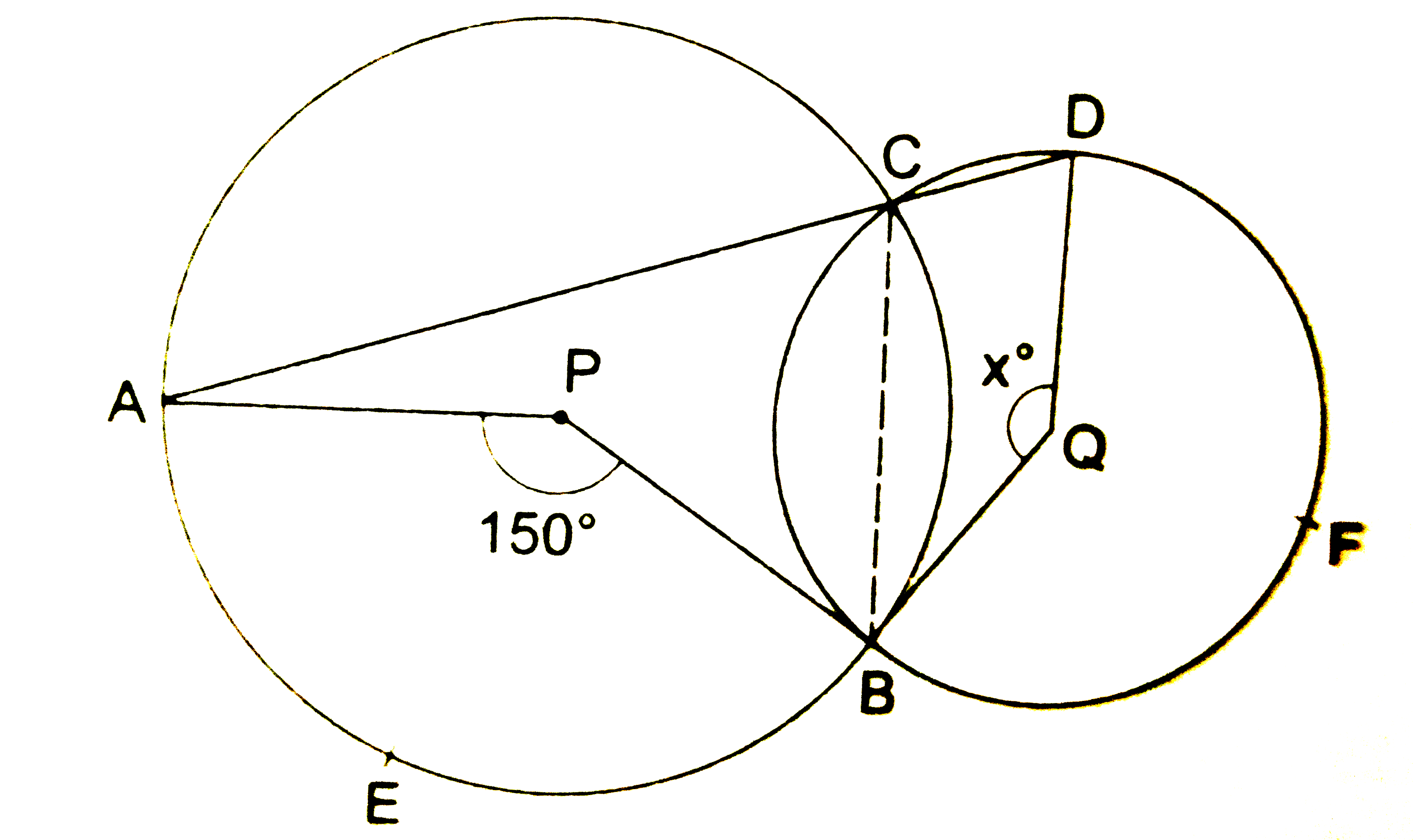
If ∠APB=150∘ and ∠BQD=x∘ , find the value of x.
Video Solution
Text Solution
Join BC.
We know that the angle made by than arc at the centre is twice the angle made by the arc at the point on the remaining part of the circle.
∴∠ACB=12∠APB=(12×150∘)=75∘
Now, ACD being a straight line, we have
∠ACB+∠BCD=180∘
⇒75∘+∠BCD=180∘⇒∠BCD=180∘−75∘=105∘
Similarly, for the second circle, we have
∠BCD=12 reflex ∠BQD.
[ angle made by the major arc BFD at the centre=2∠BCD]
⇒105∘=12(360∘−x∘)=x=150
Hence, x=150
|
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12C
26 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)
5 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
In the given figure, O is the centre of the circle, ∠ACB=54∘ and BCF is a straight line. Find x.
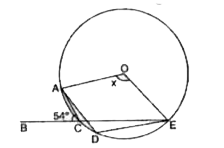 A126∘B54∘C108∘D90∘
A126∘B54∘C108∘D90∘Two circles with centres P and Q intersect at B and C, A, D are points on the circles with centres P and Q respectively such that A, C, D are colliner. If ∠APB=130∘,and∠BQD=x∘, then the value of x is :
A65B130C195D135Two circles with centres P and Q intersect at B and C, A, D are points on the circles with centres P and Q respectively such that A, C, D are colliner. If ∠APB=130∘,and∠BQD=x∘, then the value of x is :
A65B130C195D135
If APB is a straight line then find x
View SolutionIn the figure given below,LOM is a straight line. What is the value of x?
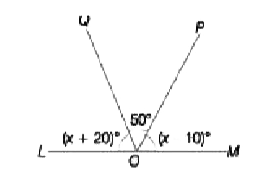
View SolutionIn the figure given below, PTU is a straight line. What is the value of x ?
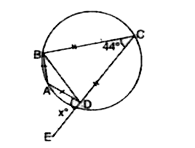
View SolutionIn the figure, CDE is a straight line and A, B, C and D are points on the circle. ∠BCD=44∘, find the value of x.
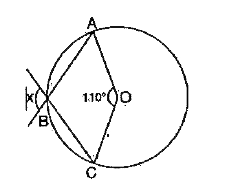
View SolutionIn the given figure, O is the centre of the circle. The value of x is
View Solution
