In the figure,
seg seg .
Complete the following activity to prove is the midpoint of seg .
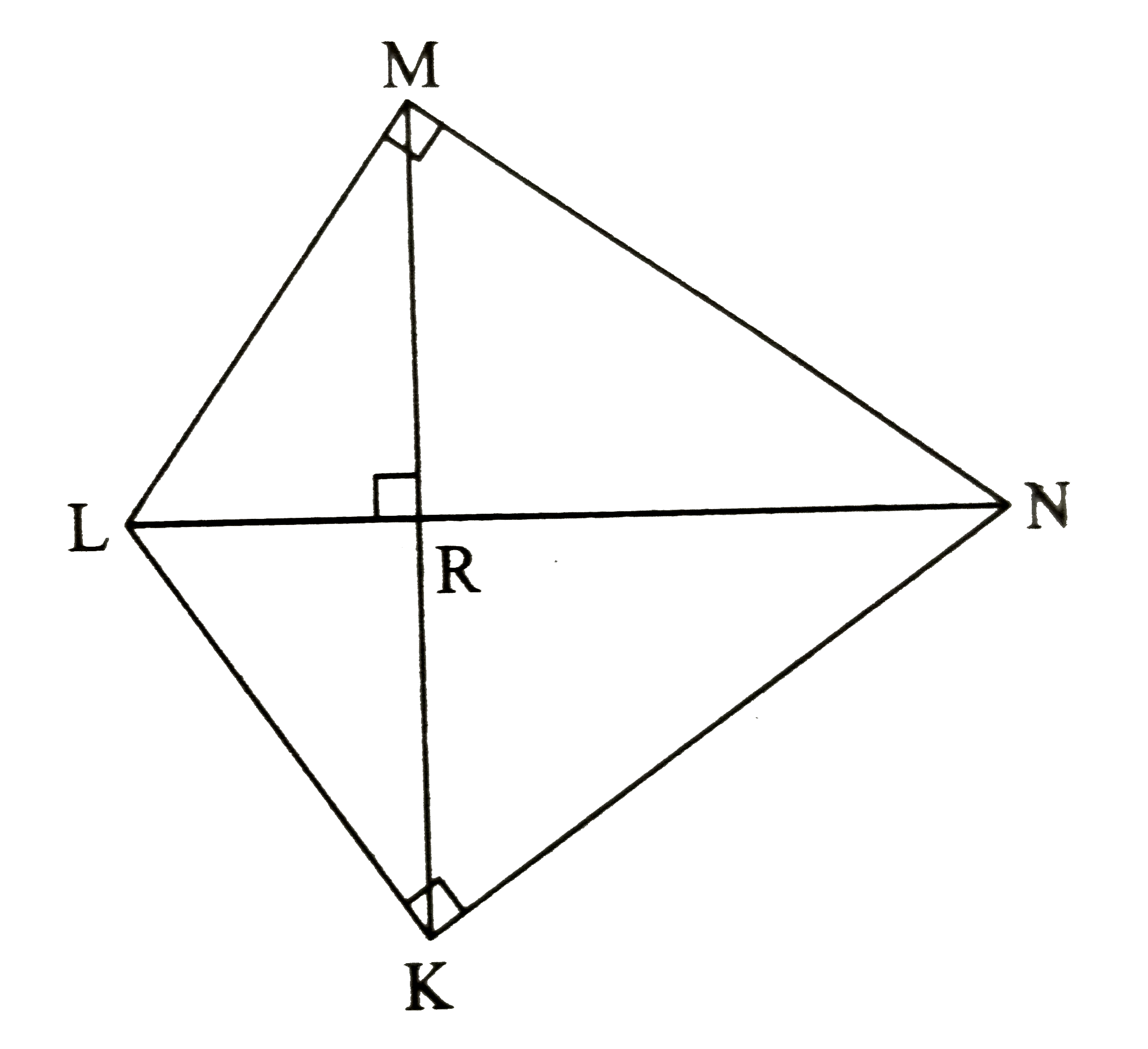
Proof: In ,
seg hypotenuse
by property of geometric mean,
In ,
seg hypotenuse
by property of geometric mean,
From and , we get
.
is the midpoint of seg .
Step by step video & image solution for In the figure, /_LMN=/_LKN=90^(@) seg MK bot seg LN. Complete the following activity to prove R is the midpoint of seg MK. Proof: In DeltaLMN, /_LMN=90^(@) seg MR bot hypotenuse LN :. by property of geometric mean, MR^(2)=squarexxRN In DeltaLKN, /_LKN=90^(@) seg KR bot hypotenuse LN :. by property of geometric mean, KR^(2)=LRxxsquare From (1) and (2), we get MR^(2)=square :. MR=square. :. R is the midpoint of seg MK. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - Assignment 3.412videos
PYTHAGORAS THEOREM
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - Assignment 3.55videos
PYTHAGORAS THEOREM
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - Assignment 3.26videos
PYTHAGORAS THEOREM
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - ASSIGNEMENT 5.412videos
PROBABILITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATION EXERCISE - CHALLENGIN QUESTIONS2videos
QUADRATIC EQUATION
Similar Questions
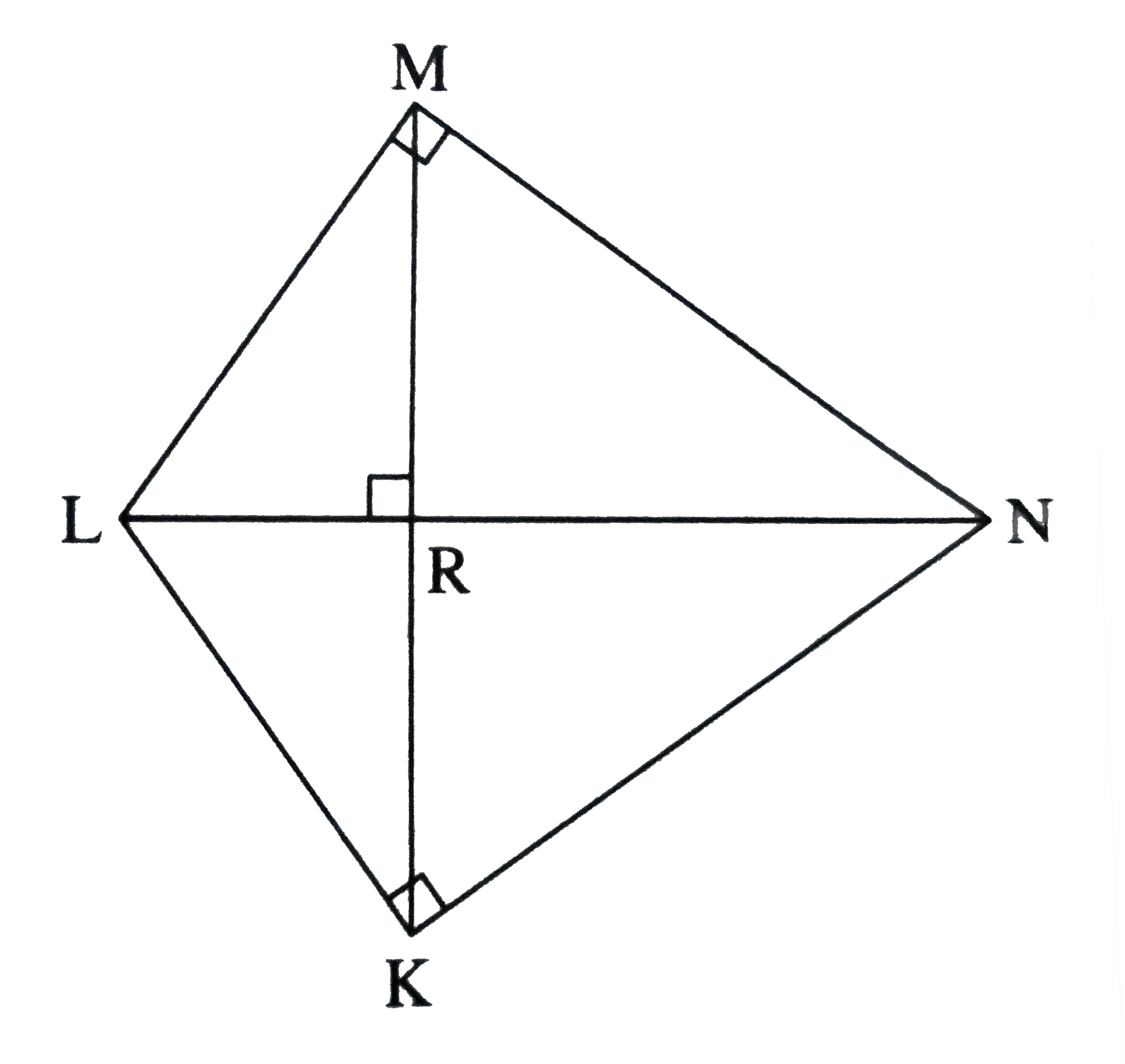
In the figure , ∠LMN=∠LKN=90∘
seg MK ⊥ seg LN .
Complete the following activtiy
to prove R is the midpoint of seg MK .
 View Solution
View SolutionIn the figure, ∠DFE=90∘, seg FG⊥ side DE, DG=8, FG=12 then complete the following activity to find the length of seg DE.
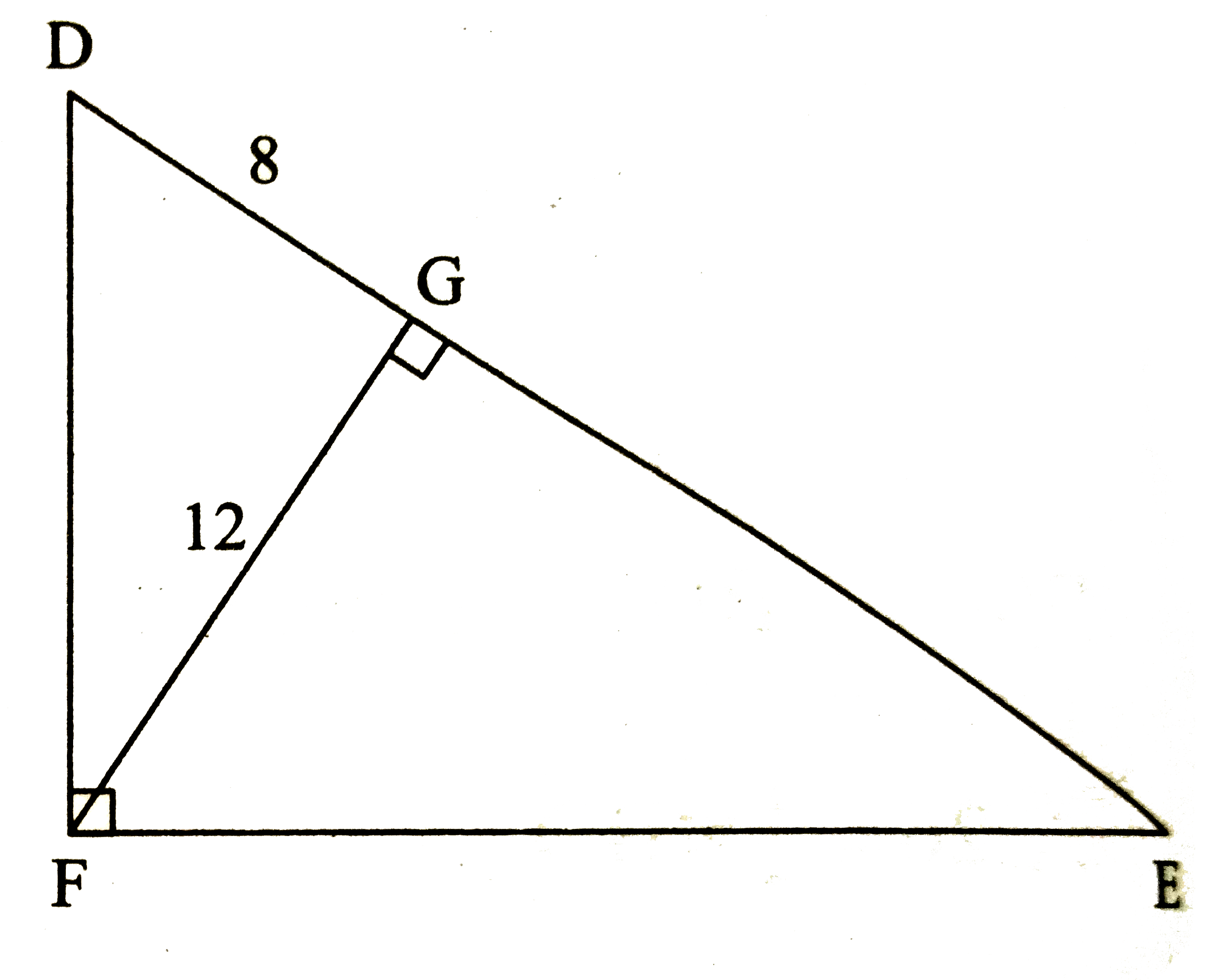
In ΔDFE, ∠DFE=90∘,
seg FG⊥ hypotenuse DE
∴ by theorem of geometric mean,
FG2=□×EG
∴122=□×EG
EG=12×12□
∴EG=□
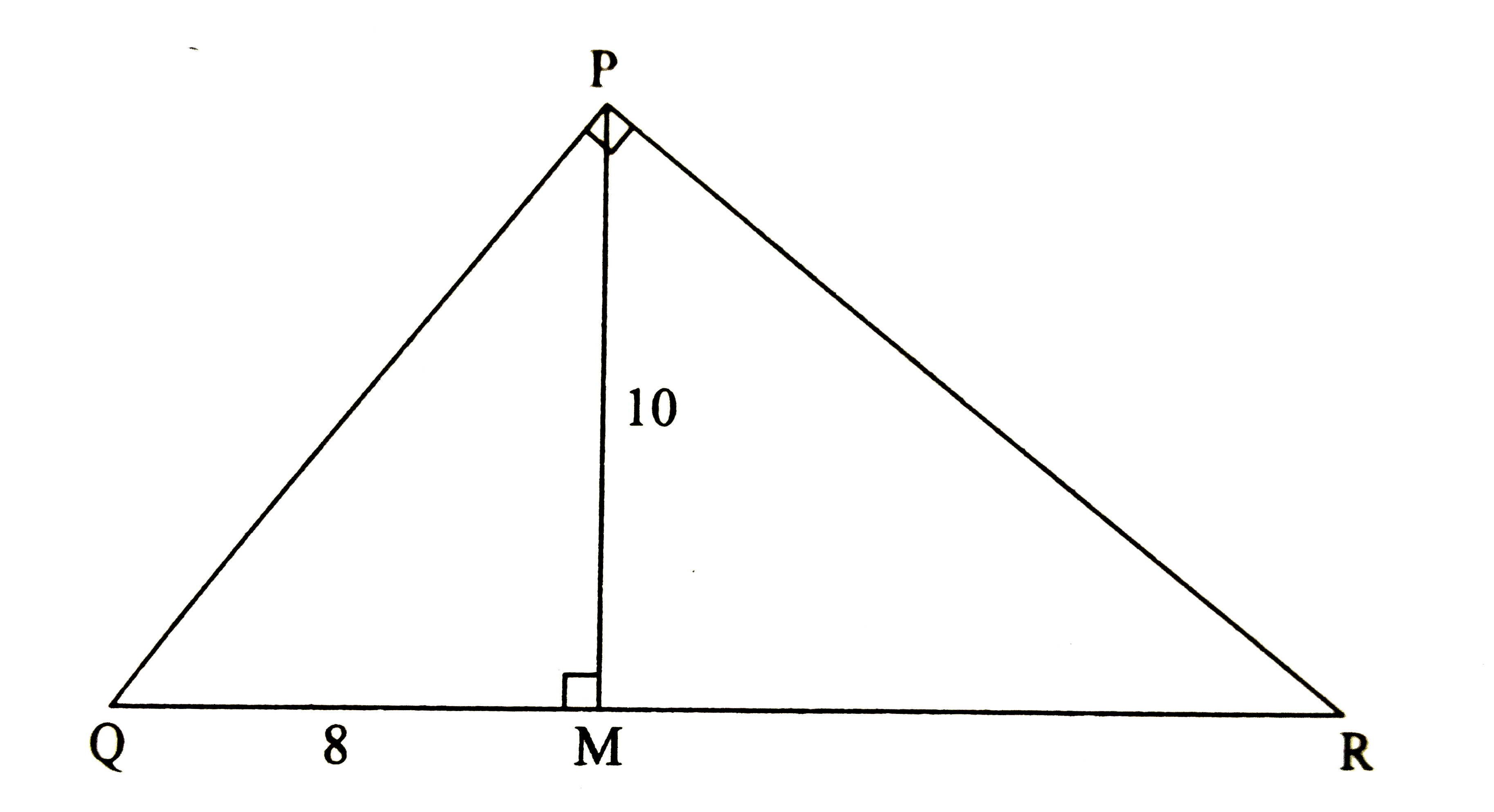
DE=DG+GE=8+□=□View SolutionIn the figure, ∠QPR=90∘, seg PM⊥ seg QR and Q−M−R, PM=10. QM=8, find QR.
 View Solution
View SolutionIn ΔPQR,∠PQR=90∘andsegQS⊥ hypotnuse PR,-P-S-R,then
View SolutionIn the figure, ∠ABC=90∘ and seg Bd⊥ side AC, A−D−C then by property of geometric mean. BD2=□×□. Fill in the boxes with the correct answer.
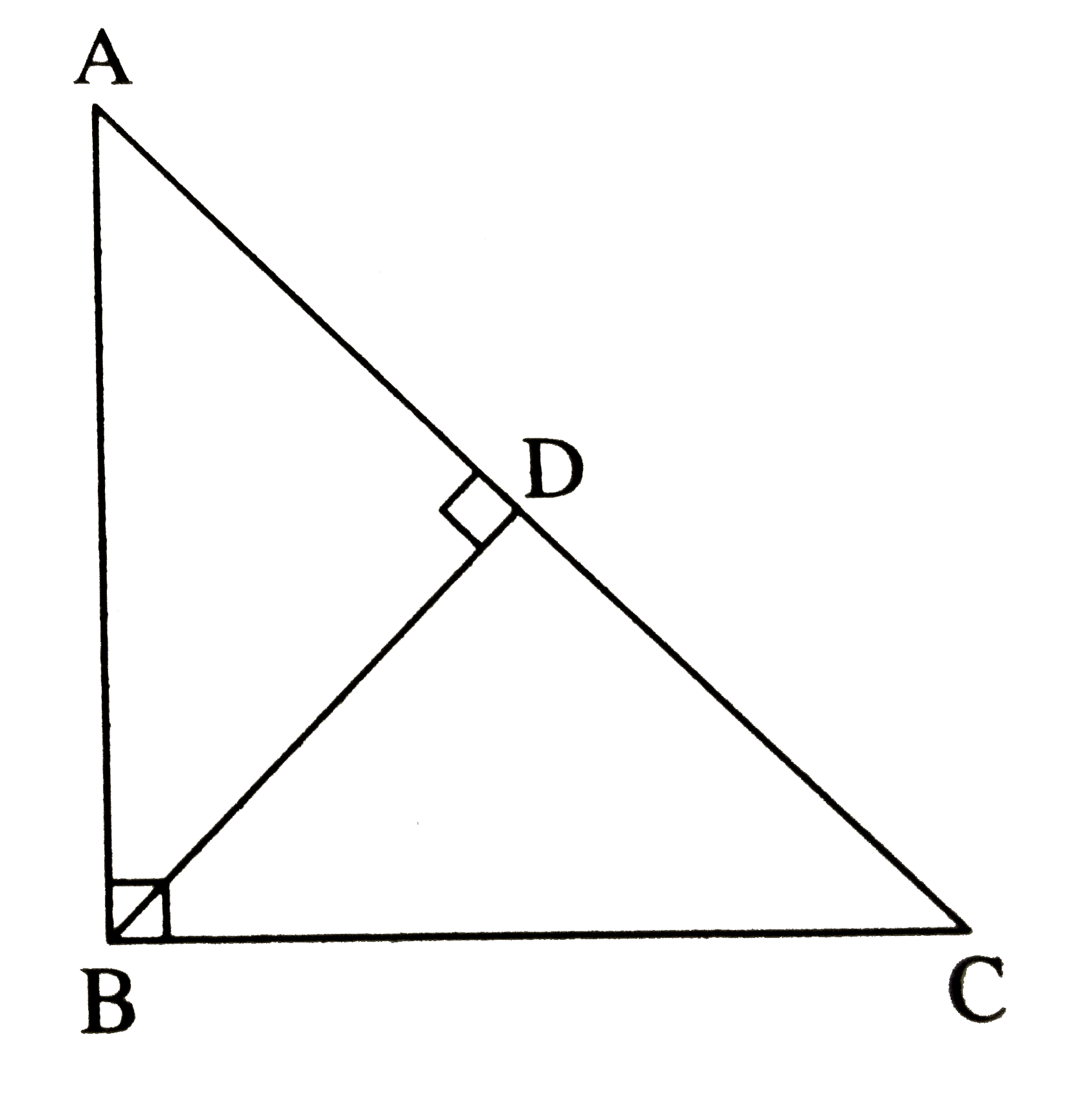 View Solution
View Solution.Point M is the midpoint of Seg AB.If AB=8 then find the length of AM.
View SolutionIn the adjoining figure, seg XY ||seg BC, then which of the following statements is true?
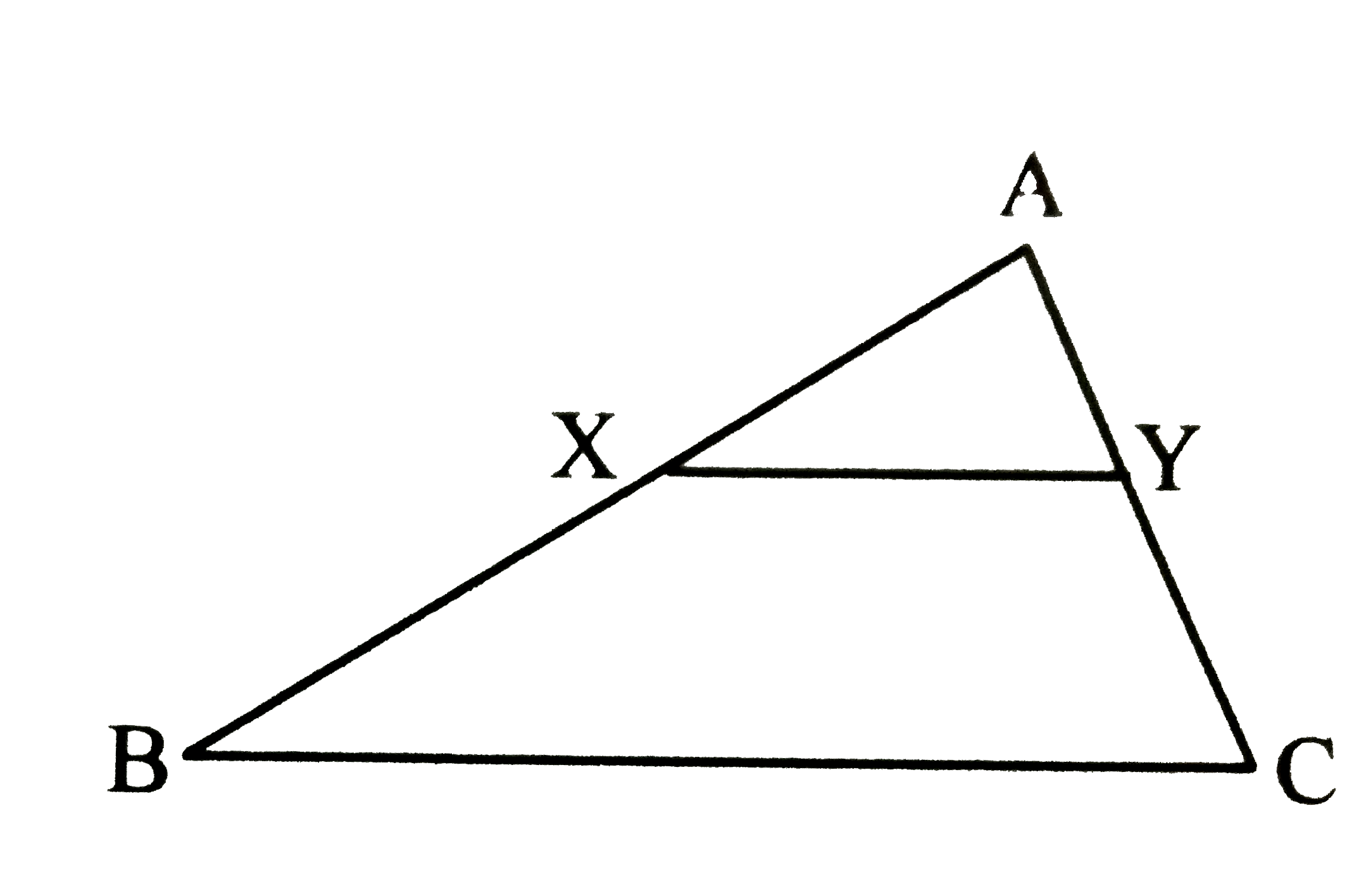 View Solution
View SolutionIn the figure, AD=17, AB=10, BC=15. ∠ABC=∠BCD=90∘ seg AE⊥ side CD then find the length of (i)AE (ii)DE (iii)DC.
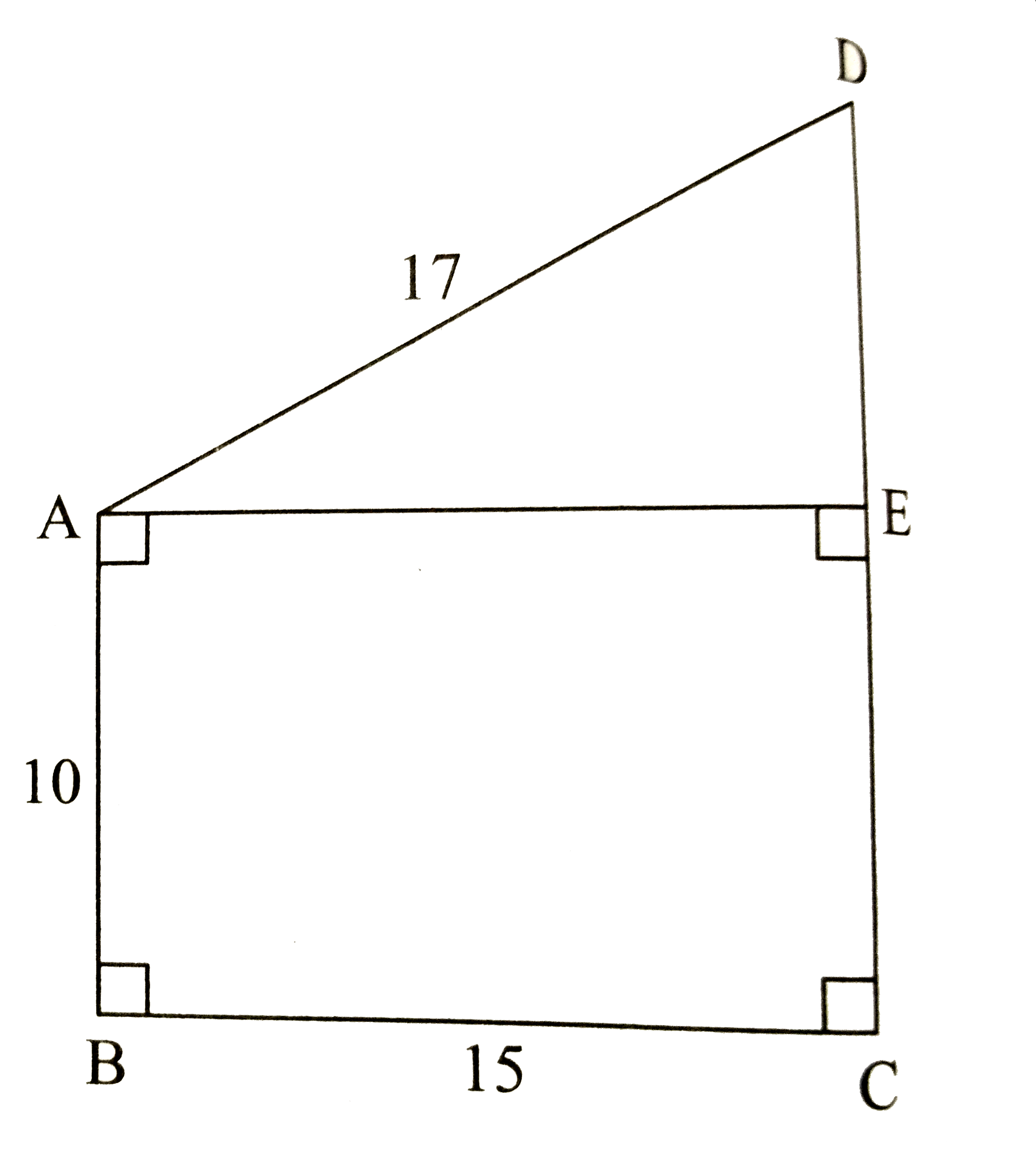 View Solution
View SolutionIn ΔPQR,∠PQR=90∘,segQS⊥segPR, then find x,y,z.
View SolutionIn ΔPQR,∠PQR=90∘,
seg QS⊥ seg PR then find x,y,z.View Solution

