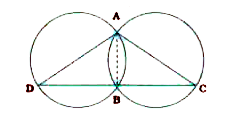
In the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circles. Prove that PBQ is a straight line.

Join AB.
In first circle,
AP is the diameter of the circle.
∴∠ABP=90∘ (angle in a semi-circle)
In second circle,
AQ is the diameter of the circle.
∴∠ABQ=90∘
Now, ∠ABP+∠ABQ=90∘+90∘
⇒∠PBQ=180∘
⇒PBQ is a straight line.
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
In the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circles. Prove that PBQ is a straight line.

View SolutionTwo circles intersect at two points A and B . AD and AC are diameters to the two circles .Prove that B lies on the line segment DC.
View Solution
Knowledge Check
Two circles intersect each other at P and Q. PA and PB are two diameters. Then ∠AQB is
A120∘B135∘C160∘D180∘
Two circles intersect each other at point P an Q. If PA and PB are two diameter then find ∠AQB.
View SolutionTwo circles intersect at two points A and B. AD and AC are diameters to the two circles (see Fig.10.34). Prove that B lies on the line segment DC.
View SolutionTwo circle intersect in AandBandACandAD are respectively the diameters of the circles. Prove that C,B,D are collinear.
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.

View SolutionIn the figure, two circles intersect each other at points A and B . C is a point on the smaller circle. Secant CA and secant CB of the smaller circle intersect the bigger circle at points D and E respectively then prove : seg DE ∣∣ line CF
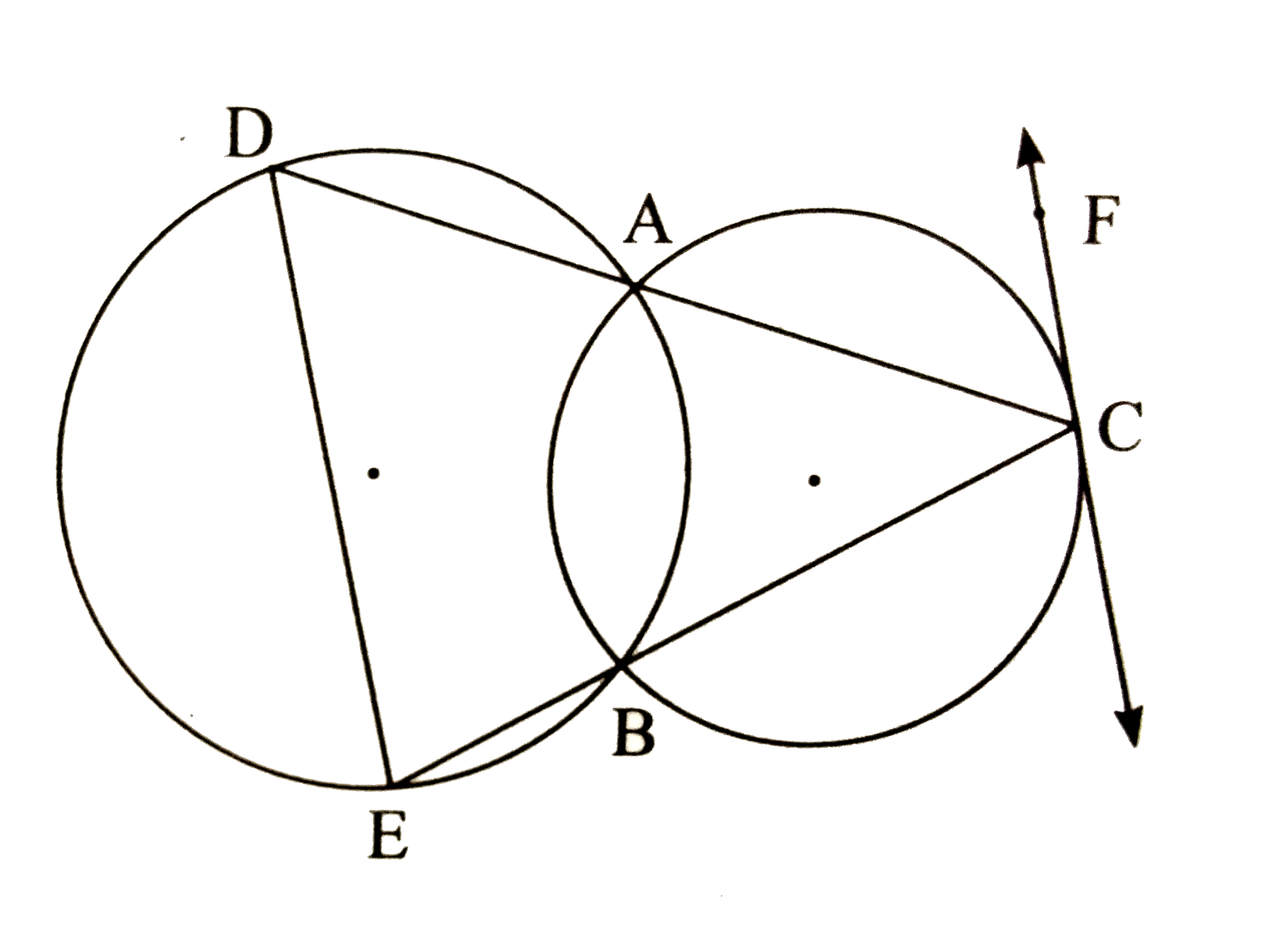
View SolutionIn figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that □ ABCD is cyclic.

View SolutionIn the fig. two circles intersect each other in point A and B. Secants through the point A intersect the circles in point P,Q and R,S. Line PR and SQ intersect in T. (i) PTQ and PBQ are supplementary. (ii) □ BSTR is cyclic quadrilateral.
View Solution
