In the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.

Step by step video & image solution for In the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Additional Problems for Practice32videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Chapter 6: Statistics4videos
CHALLENGING QUESTIONS
- BOOK - TARGET PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - CHAPTER ASSESSMENT19videos
CO-ORDINATE GEOMETRY
Similar Questions
In figure, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P,Q. Prove that, ∠PRQ+∠PSQ=180∘.
 View Solution
View SolutionIn the fig. two circles intersect each other in point A and B. Secants through the point A intersect the circles in point P,Q and R,S. Line PR and SQ intersect in T. (i) PTQ and PBQ are supplementary. (ii) □ BSTR is cyclic quadrilateral.
View SolutionIn the figure, two circles intersect each other at points A and B . C is a point on the smaller circle. Secant CA and secant CB of the smaller circle intersect the bigger circle at points D and E respectively then prove : seg DE ∣∣ line CF
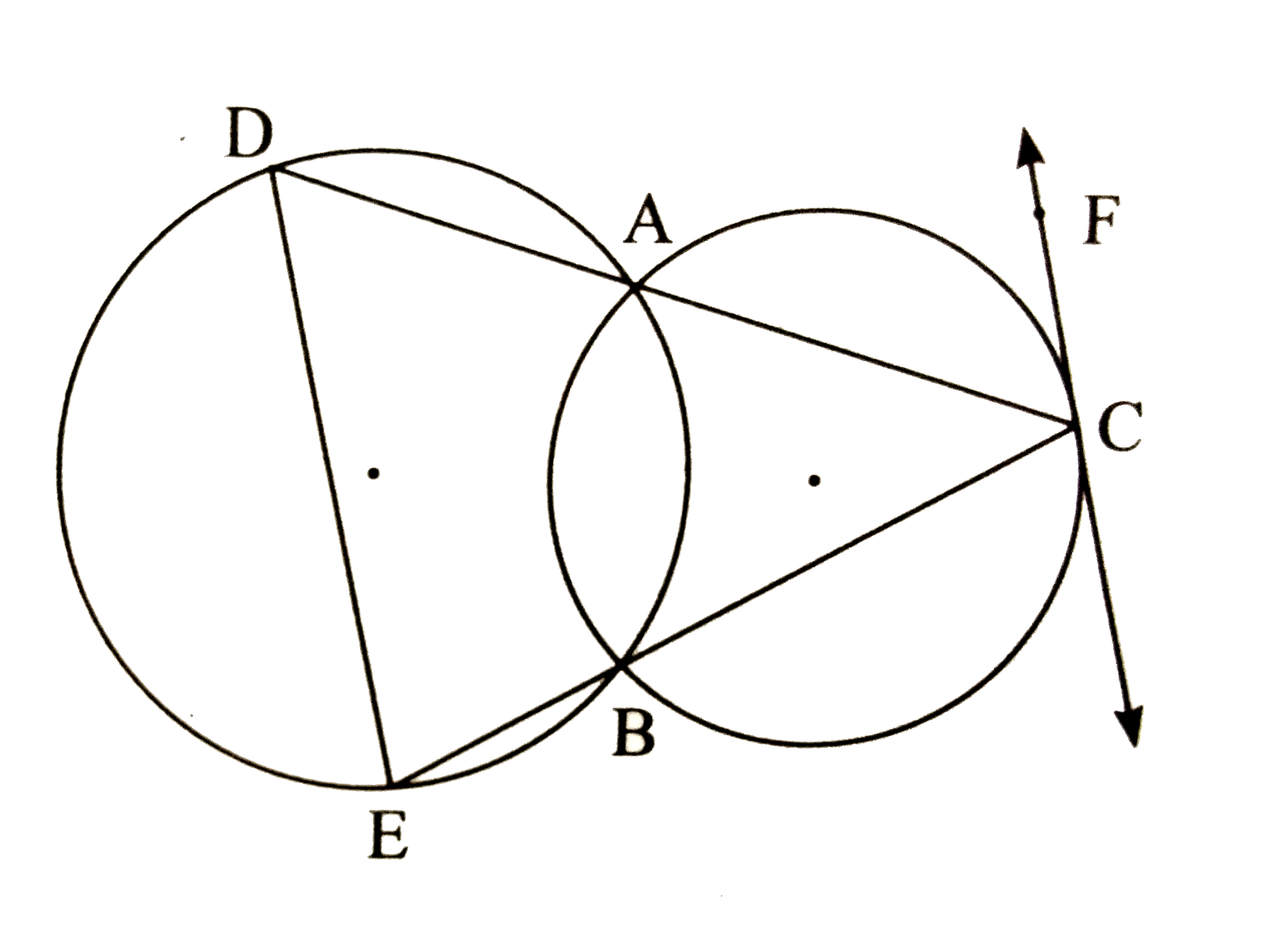 View Solution
View SolutionIn figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that □ ABCD is cyclic.
 View Solution
View SolutionTwo circles intersect each other at point P an Q. If PA and PB are two diameter then find ∠AQB.
View SolutionIn the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circles. Prove that PBQ is a straight line.
 View Solution
View SolutionAs per the figure, two circles intersect each other at points P and Q. Point A is on PQ produced and AMD and ASR are the secants to the circles. If AM = 3, MD = 5, AS = 4, The value of SR is :
View SolutionTwo circles intersect at two points P and S. QR is a tangent to the two circles at Q and R. If ∠QSR=72∘, then ∠QPR=.
View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
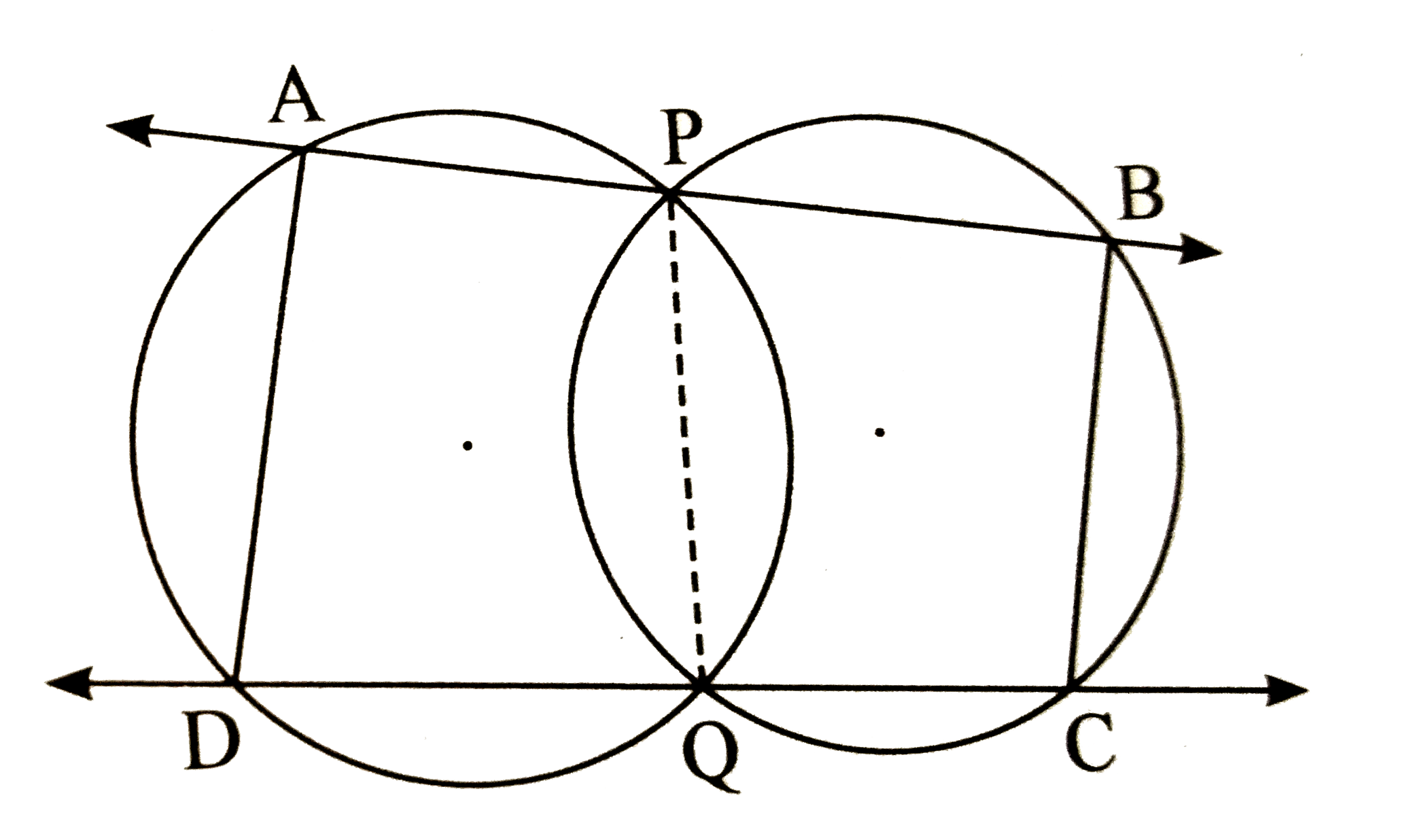 View Solution
View SolutionIn the figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that : seg SQ ∣∣ seg RP.
 View Solution
View Solution

