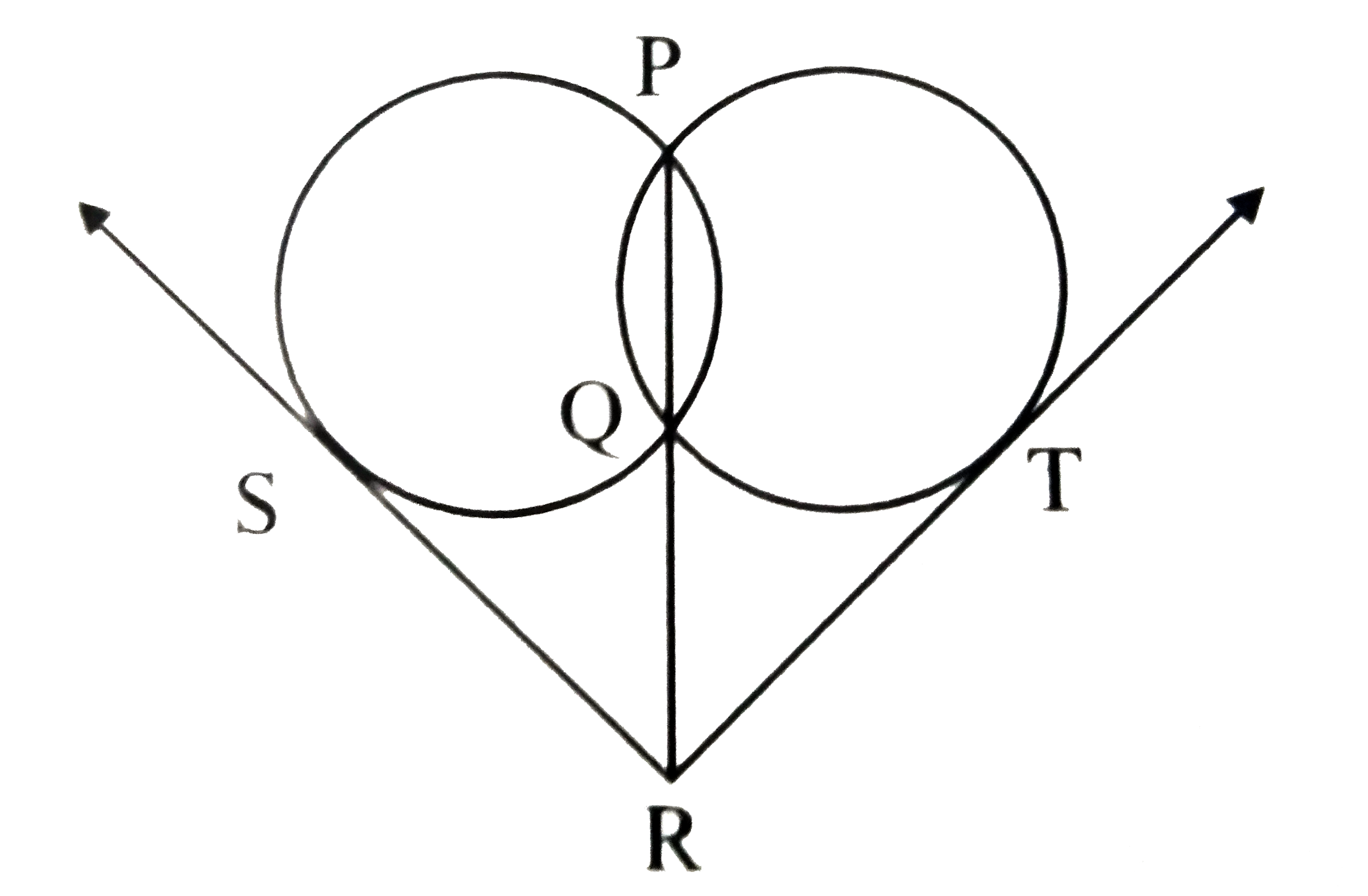
In figure, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P,Q. Prove that, ∠PRQ+∠PSQ=180∘.

The correct Answer is:∴∠PRQ+∠PSQ=180∘ ……..( Angle addition postulate )
Step by step video & image solution for In figure, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P,Q. Prove that, /_PRQ+/_PSQ=180^(@). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - Challenging Questions
10 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.5
6 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
In figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that □ ABCD is cyclic.

View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.
View Solution
Knowledge Check
Two circles touch each other externally at point A and PQ is a direct tangent which touch circle at P and Q respectively then ∠PAQ = ?
A45∘B90∘C80∘D100∘Two circles touch each other externally at a point P and a direct common tangent touches the circles at the points Q and R respectively. Then ∠QPR is
A45∘B180∘C90∘D60∘
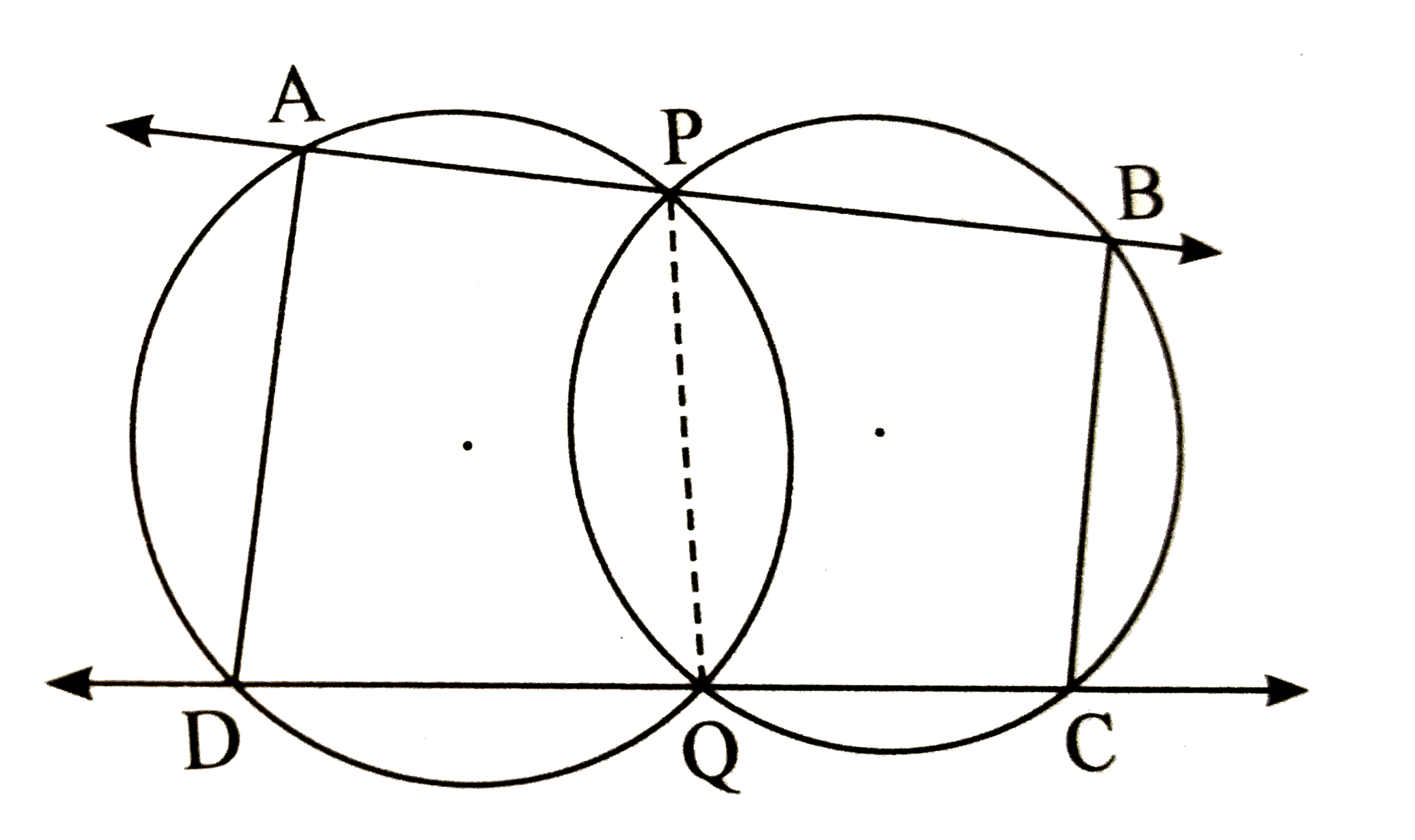
Two circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
View SolutionIn the given figure two circles touch each other at the point C. Prove that the common tangent at P and Q.
View SolutionIn figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that : seg SQ || seg RP.

View SolutionTwo circles intersect each other at point P an Q. If PA and PB are two diameter then find ∠AQB.
View SolutionIn the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circles. Prove that PBQ is a straight line.

View SolutionIn the figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that : seg SQ ∣∣ seg RP.

View Solution
