In the following figure, BD is parallel to CA, E is mid-point of CA and BD = 12 CA.
Prove that : ar.(ΔABC)=2×ar.(ΔDBC)
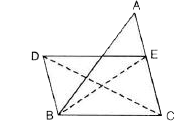
Step by step video & image solution for In the following figure, BD is parallel to CA, E is mid-point of CA and BD = (1)/(2) CA. Prove that : ar.(DeltaABC)=2xxar.(DeltaDBC) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(B)
16 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
Similar Questions
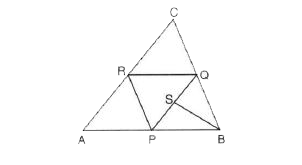
The following figure shows a triangle ABC in which P, Q and R are mid-points of sides AB, BC and CA respectively. S is mid-point of PO.
Prove that : ar.(ΔABC)=8×ar.(ΔQSB)
View SolutionIn the figure of question 2, if E is the mid point of median AD, then prove that :
Area(ΔABE)=14Area(ΔABC).
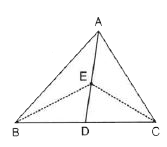
View SolutionIn the figure of question 2, if E is the mid point of median AD, then prove that :
Area(ΔABE)=14Area(ΔABC).

View SolutionBalance the following equations.
Ca+O2→CaO
View SolutionIn the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of ΔBOEandΔABC

View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) AB+BC+CD+DA<2(AC+BD)
(b) AB+BC+CD+DA>(AC+BD)

View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB of the equilateral ΔABC. Prove that ΔDEF is also an equilateral triangle.

View SolutionIn the adjoining figure, P is an interior point of ΔABC. Then prove that :
AB+BC+CA<2(PA+PB+PC)

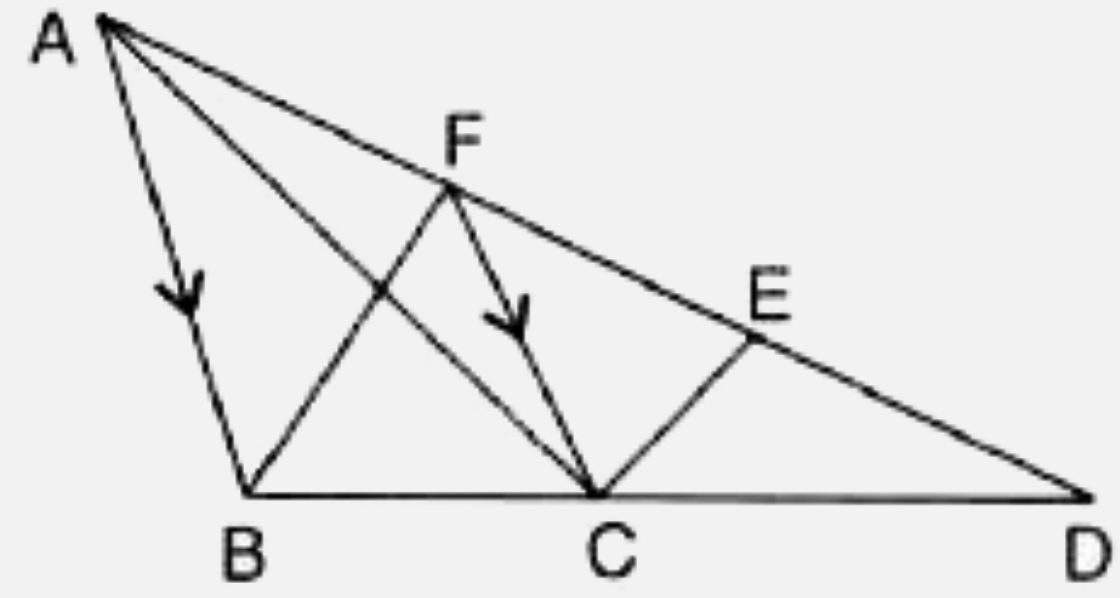
View SolutionIn the following figure, F and E are points on the side AD of the triangle ABD. Through F a line is drawn parallel to AB to meet BD at point C .
Prove that : ar (ΔACE)=ar (quad . BCEF )
View SolutionIn ΔABC,D is any point on side BC. Prove that
AB+BC+CA>2AD
View Solution
