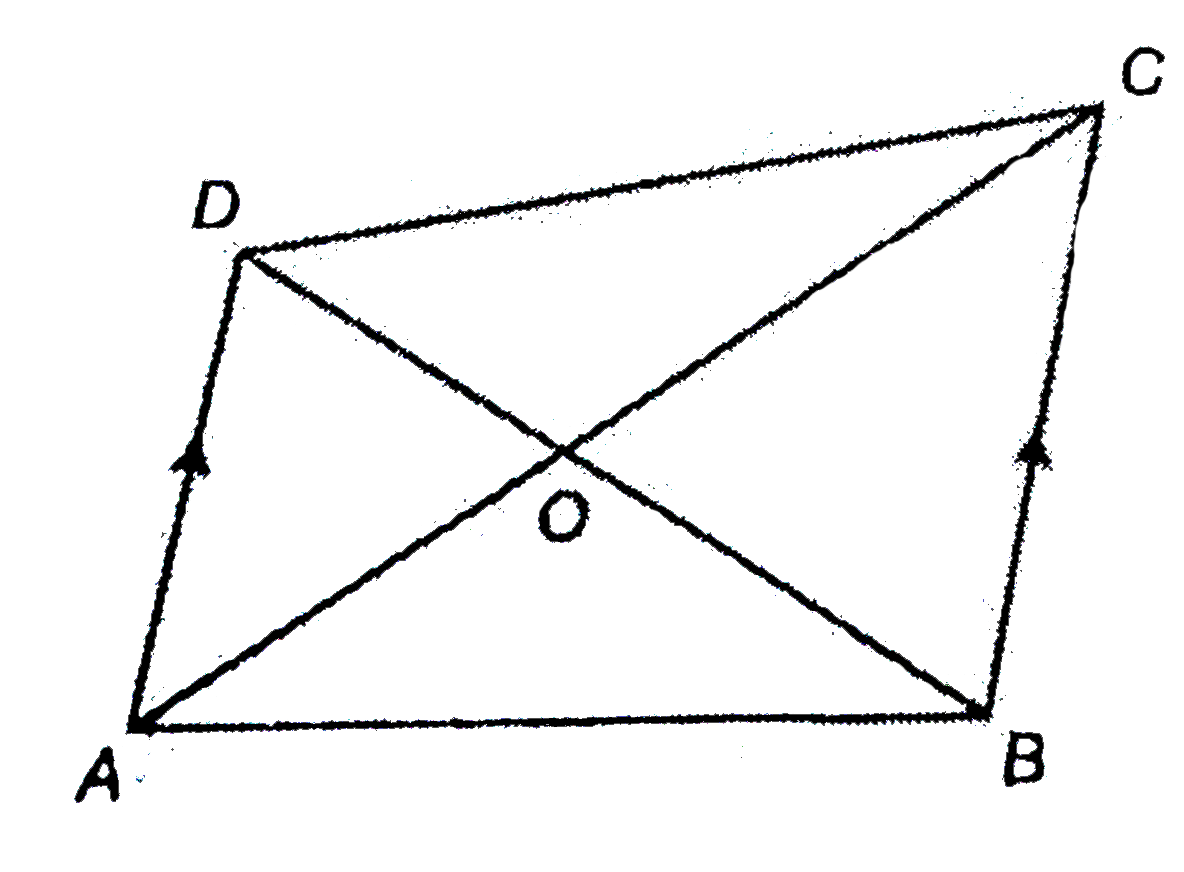
In the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) AB+BC+CD+DA<2(AC+BD)
(b) AB+BC+CD+DA>(AC+BD)

(a) We know that the sum of any two sides of a triangle is greater than the third side.
∵ In ΔOAB,OA+OB>AB...(1)In ΔOBC,OB+OC>BC...(2)In ΔOCD,OC+OD>CD...(3)In ΔODA,OD+OA>DA...(4)
OA+OB+OB+OC+OC+OD+OD+OA>AB+BC+CD+DA
⇒ 2OA+2OB+2OC+2OD>AB+BC+CD+DA
⇒ 2(OA+OC)+2(OB+OD)>AB+BC+CD+DA
⇒ 2AC+2BD>AB+BC+CD+DA
⇒ 2(AC+BD)>AB+BC+CD+DA
⇒ AB+BC+CD+DA<2(AC+BD)
(b) In ΔABC,AB+BC>AC...(5)In ΔBCD,BC+CD>BD...(6)In ΔCDA,CD+DA>AC...(7)In ΔDAB,DA+AB>BD...(8)
Adding (5), (6), (7) and (8), we get
AB+BC+BC+CD+CD+DA+DA+AB>AC+BD+AC+BD
⇒ 2(AB+BC+CD+DA)>2(AC+BD)
⇒ AB+BC+CD+DA>AC+BD
Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 7a
35 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
In the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect point O. Prove that :
AB+BC+CD+DA<2(AC+BD)

View SolutionABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
View SolutionIn the adjoining figure, ABCD is a quadrilateral in which AD∣∣BC. AC and BD intersect each other at point 'O'. Prove that:
area of ΔCOD= area of ΔABO
View SolutionABCD is quadrilateral. Is AB+BC+CD+DA<2(AC+BD)?
View SolutionThe given figure shows an equilateral triangles ABC and D is point in AC.
Prove that :
(i) AD<BD
(ii)BC>BD
View SolutionABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that AOOC=BOOD
View SolutionIn quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE:EC=BE:ED.
Show that : ABCD is a trapezium.
View SolutionIn a quadrilateral ABCD, prove that :
(i) AB+BC+CD>DA
(ii) AB+BC+CD+DA>2AC
(iii) AB+BC+CD+DA>2BD
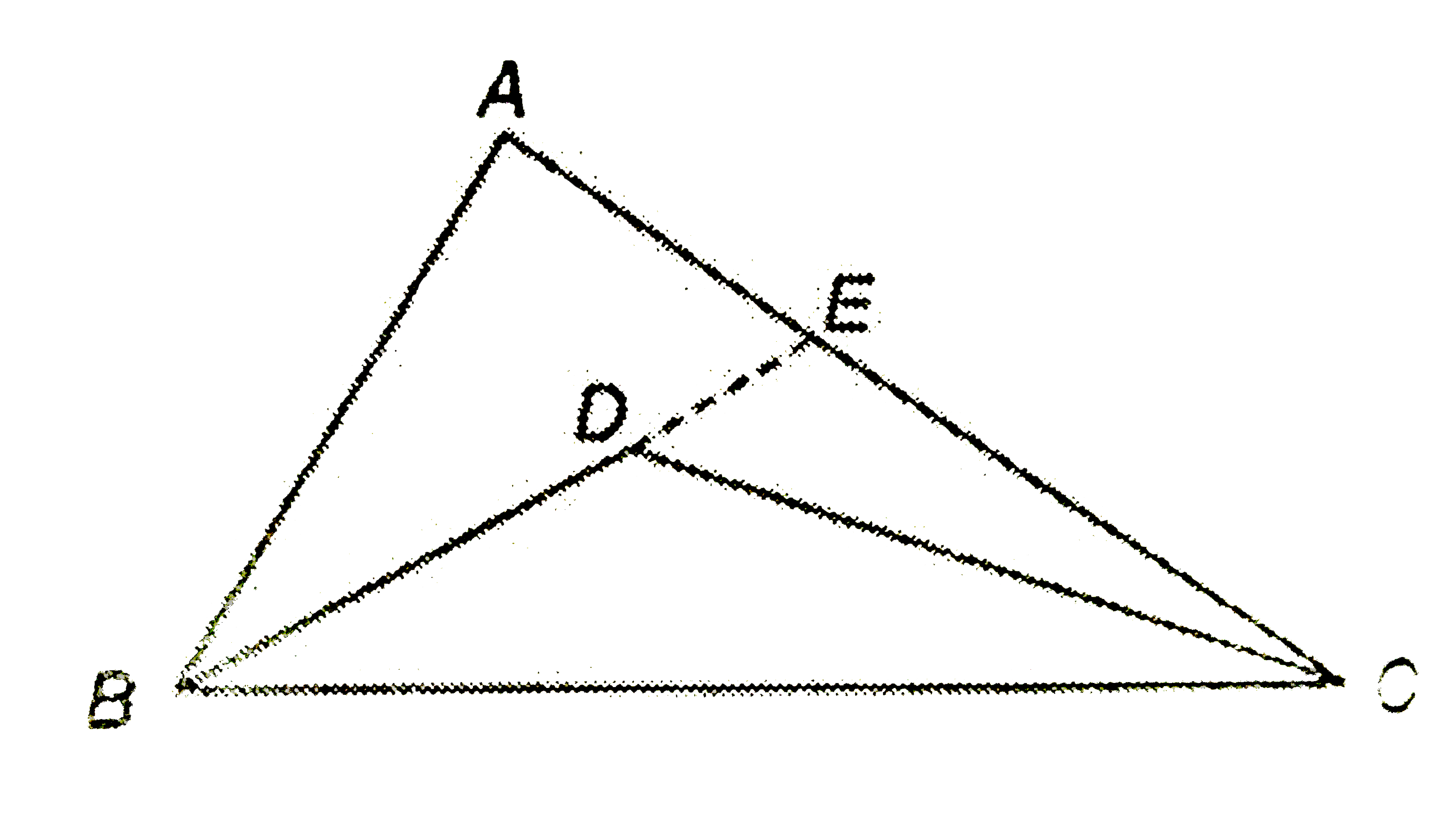
View SolutionIn the adjoining figure, ABC is a triangle and D is any point in its interior. Show that BD+DC<AB+AC.
View SolutionIn trapezium ABCD, side AB is parallel to side DC. Diagonals AC and BD intersect at point P. Prove that triangles APD and BPC are equal in area.
View Solution
