In the figure of question 2, if E is the mid point of median AD, then prove that :
Area(ΔABE)=14Area(ΔABC).
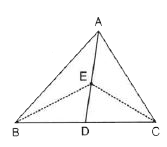
Step by step video & image solution for In the figure of question 2, if E is the mid point of median AD, then prove that : "Area" (DeltaABE)=(1)/(4) "Area" (DeltaABC). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(A)
36 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
Similar Questions
In the given figure, AD is median of ΔABC and E is any point on median AD. Prove that Area (ΔABE) = Area (ΔACE)
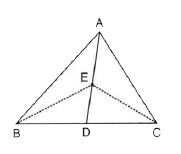
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (BED)=14ar (ABC)
View SolutionIn the given figure, AD//BE//CF.
prove that :
area (ΔAEC)
= area (ΔDBF)
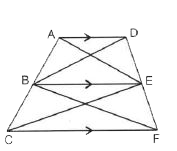
View SolutionIn a ABC, E is the mid-point of median AD. Show that ar (BED)=14ar (ABC)
View SolutionIn the adjoining figure, DE∣∣BC. Prove that area (ΔACD)= area (ΔABE)

View SolutionIn the adjoining figure, BD = DC and AE = ED. Prove that
area of ΔACE=14 area of ΔABC
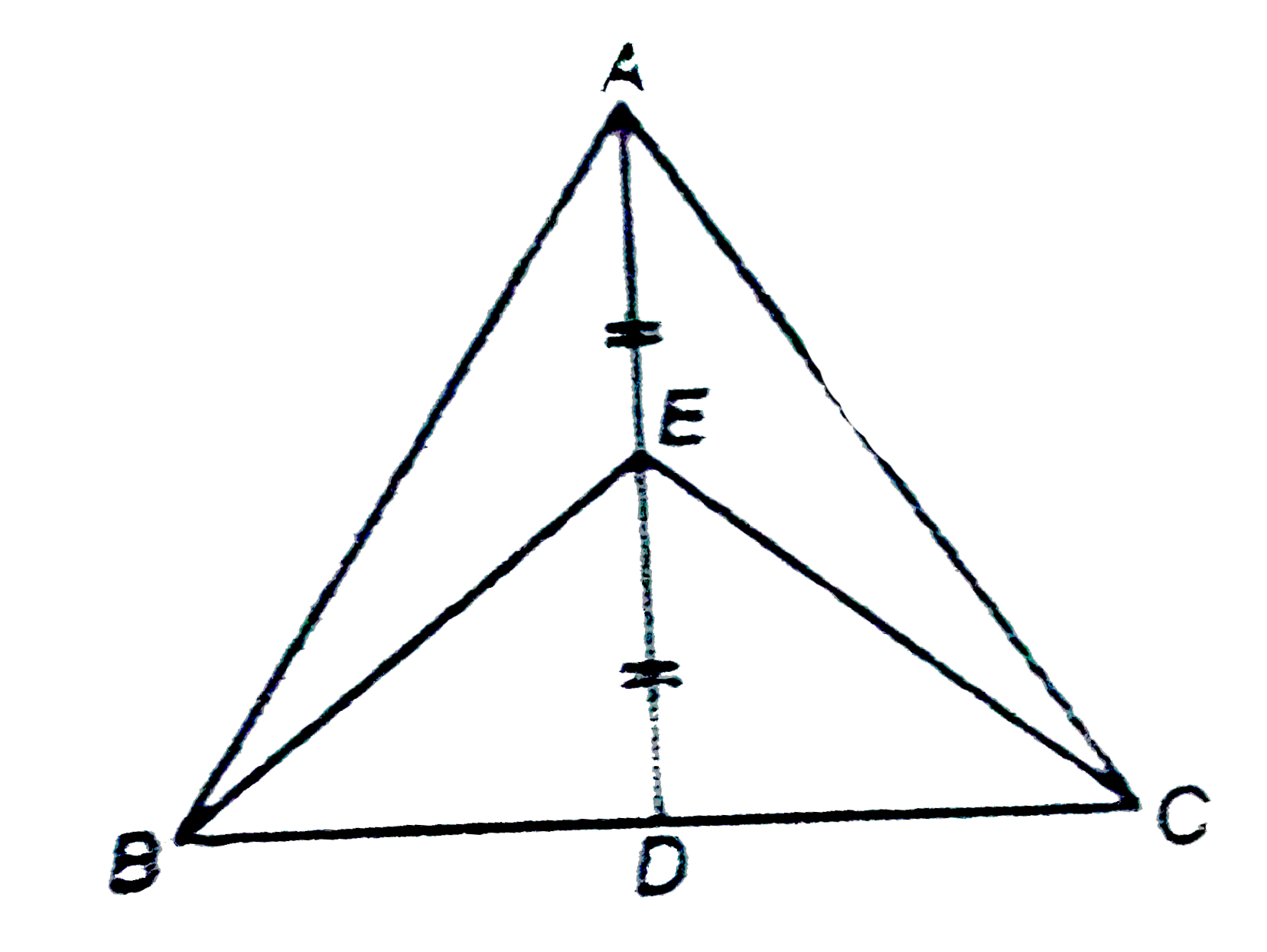
View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View SolutionIn ΔABC, AD divides BC in thr ratio m:n. Show that Area(ΔABD)Area(ΔADC)=mn
View SolutionIn the adjoining figure, AD is the median of ΔABC and X be any point on side AD. Prove that:
area (ΔABX)= area (ΔACX)

View SolutionThe medians of ΔABC intersect at point G. Prove that:
area of ΔAGB=13× area of ΔABC
View Solution
