In the following pairs of triangle (Fig. 12 to 15), the lengths of the sides are indicated along sides. By applying SSS condition, determine which are congruent. State the result in symbolic form.
To determine which pairs of triangles are congruent using the SSS (Side-Side-Side) condition, we will follow these steps:
1. Identify the Triangles:
We have two triangles, Triangle ABC and Triangle DEF.
2. List the Side Lengths:
- For Triangle ABC:
- AB = 4.5 cm
- AC = 4 cm
- BC = 6 cm
- For Triangle DEF:
- DE = 4.5 cm
- DF = 4 cm
- EF = 6 cm
3. Compare the Corresponding Sides:
- Compare AB and DE:
- AB = 4.5 cm and DE = 4.5 cm → AB = DE
- Compare AC and DF:
- AC = 4 cm and DF = 4 cm → AC = DF
- Compare BC and EF:
- BC = 6 cm and EF = 6 cm → BC = EF
4. Apply the SSS Condition:
Since all three pairs of corresponding sides are equal (AB = DE, AC = DF, BC = EF), we can conclude that Triangle ABC is congruent to Triangle DEF by the SSS condition.
5. State the Result in Symbolic Form:
- Triangle ABC ≅ Triangle DEF (using the symbol "≅" to denote congruence).
6. CPCT (Corresponding Parts of Congruent Triangles):
Since the triangles are congruent, we can also state that their corresponding angles are equal:
- Angle A ≅ Angle D
- Angle B ≅ Angle E
- Angle C ≅ Angle F
Final Result:
Triangle ABC ≅ Triangle DEF, and by CPCT:
- Angle A ≅ Angle D
- Angle B ≅ Angle E
- Angle C ≅ Angle F
We have two triangles, Triangle ABC and Triangle DEF.
- For Triangle ABC:
- AB = 4.5 cm
- AC = 4 cm
- BC = 6 cm
- For Triangle DEF:
- DE = 4.5 cm
- DF = 4 cm
- EF = 6 cm
- Compare AB and DE:
- AB = 4.5 cm and DE = 4.5 cm → AB = DE
- Compare AC and DF:
- AC = 4 cm and DF = 4 cm → AC = DF
- Compare BC and EF:
- BC = 6 cm and EF = 6 cm → BC = EF
Since all three pairs of corresponding sides are equal (AB = DE, AC = DF, BC = EF), we can conclude that Triangle ABC is congruent to Triangle DEF by the SSS condition.
- Triangle ABC ≅ Triangle DEF (using the symbol "≅" to denote congruence).
Since the triangles are congruent, we can also state that their corresponding angles are equal:
- Angle A ≅ Angle D
- Angle B ≅ Angle E
- Angle C ≅ Angle F
Triangle ABC ≅ Triangle DEF, and by CPCT:
- Angle A ≅ Angle D
- Angle B ≅ Angle E
- Angle C ≅ Angle F
Topper's Solved these Questions
Similar Questions
In each of the following pairs of triangles the measure of some parts are indicated along. Side. By the application of SAS congruence condition, state which are congruent. State the result in symbolic form.
View SolutionIn the following pairs of triangle (Fig.10), by applying SSS condition, state which are congruent. State the result in symbolic form:
View SolutionFig.33, the measure of some parts are indicated along side. By applying ASA congruence condition, state whether they are congruent. State the answer in symbolic form.
View SolutionIn each of the following pairs of right triangles, the measure of some parts are indicated along side. State by the application of RHS congruence condition which are congruent. State each result in symbolic form.
View SolutionWhich of the following pairs of triangle are congruent by ASA condition?
View SolutionIn fig. 11, the length (in cm) of each side has been indicated along the side. State for each triangle whether it is scalene, isosceles or equilateral:
View SolutionState giving reasons, which of the following are pairs of congruent triangles. Write down the names of triangles with congruent sign in each case, wherever they are congruent.
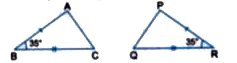
View SolutionState giving reasons, which of the following are pairs of congruent triangles. Write down the names of triangles with congruent sign in each case, wherever they are congruent.
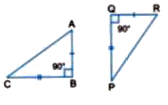
View SolutionState giving reasons, which of the following are pairs of congruent triangles. Write down the names of triangles with congruent sign in each case, wherever they are congruent.

View SolutionState giving reasons, which of the following are pairs of congruent triangles. Write down the names of triangles with congruent sign in each case, wherever they are congruent.
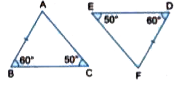
View Solution
