Δ ABC and Δ ABD are on a common base AB, and AC = BD and BC = AD as shown in Fig. 18. Which of the following statements is true? ΔABC≅ΔABD ΔABC≅ΔADB ΔABC≅ΔBAD
To solve the problem, we need to analyze the given information about triangles ABC and ABD.
1. Identify the Given Information:
- We have two triangles: ΔABC and ΔABD.
- They share a common base AB.
- It is given that AC = BD and BC = AD.
2. Understanding Triangle Congruence:
- For two triangles to be congruent, we can use the Side-Side-Side (SSS) or Side-Angle-Side (SAS) criteria.
- In this case, we can use the information provided to check for congruence.
3. Apply the Given Information:
- We know:
- AC = BD (given)
- BC = AD (given)
- AB = AB (common side, equal to itself)
4. Check for Congruence:
- By the SSS criterion, since we have:
- AC = BD
- BC = AD
- AB = AB
- We can conclude that triangles ABC and ABD are congruent.
5. Identify the Correct Statement:
- The options provided are:
- ΔABC ≅ ΔABD
- ΔABC ≅ ΔADB
- ΔABC ≅ ΔBAD
- Based on our analysis, the correct statement is ΔABC ≅ ΔABD.
Conclusion:
The correct answer is ΔABC ≅ ΔABD.
- We have two triangles: ΔABC and ΔABD.
- They share a common base AB.
- It is given that AC = BD and BC = AD.
- For two triangles to be congruent, we can use the Side-Side-Side (SSS) or Side-Angle-Side (SAS) criteria.
- In this case, we can use the information provided to check for congruence.
- We know:
- AC = BD (given)
- BC = AD (given)
- AB = AB (common side, equal to itself)
- By the SSS criterion, since we have:
- AC = BD
- BC = AD
- AB = AB
- We can conclude that triangles ABC and ABD are congruent.
- The options provided are:
- ΔABC ≅ ΔABD
- ΔABC ≅ ΔADB
- ΔABC ≅ ΔBAD
- Based on our analysis, the correct statement is ΔABC ≅ ΔABD.
The correct answer is ΔABC ≅ ΔABD.
Topper's Solved these Questions
Similar Questions
In figure, if ΔABE≅ΔACD, show that ΔADE~ΔABC.

View SolutionIn two triangles ABC and ADC, if AB=AD and BC=CD. Are they congruent?
View SolutionΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC

View SolutionIn Figure altitudes AD and CE of A B C intersect each other at the point P. Show that:(i) ΔAEP~ΔCDP (ii) ΔABD~ΔCBE (iii) ΔAEP~ΔADB(iv) ΔPDC~ΔBEC
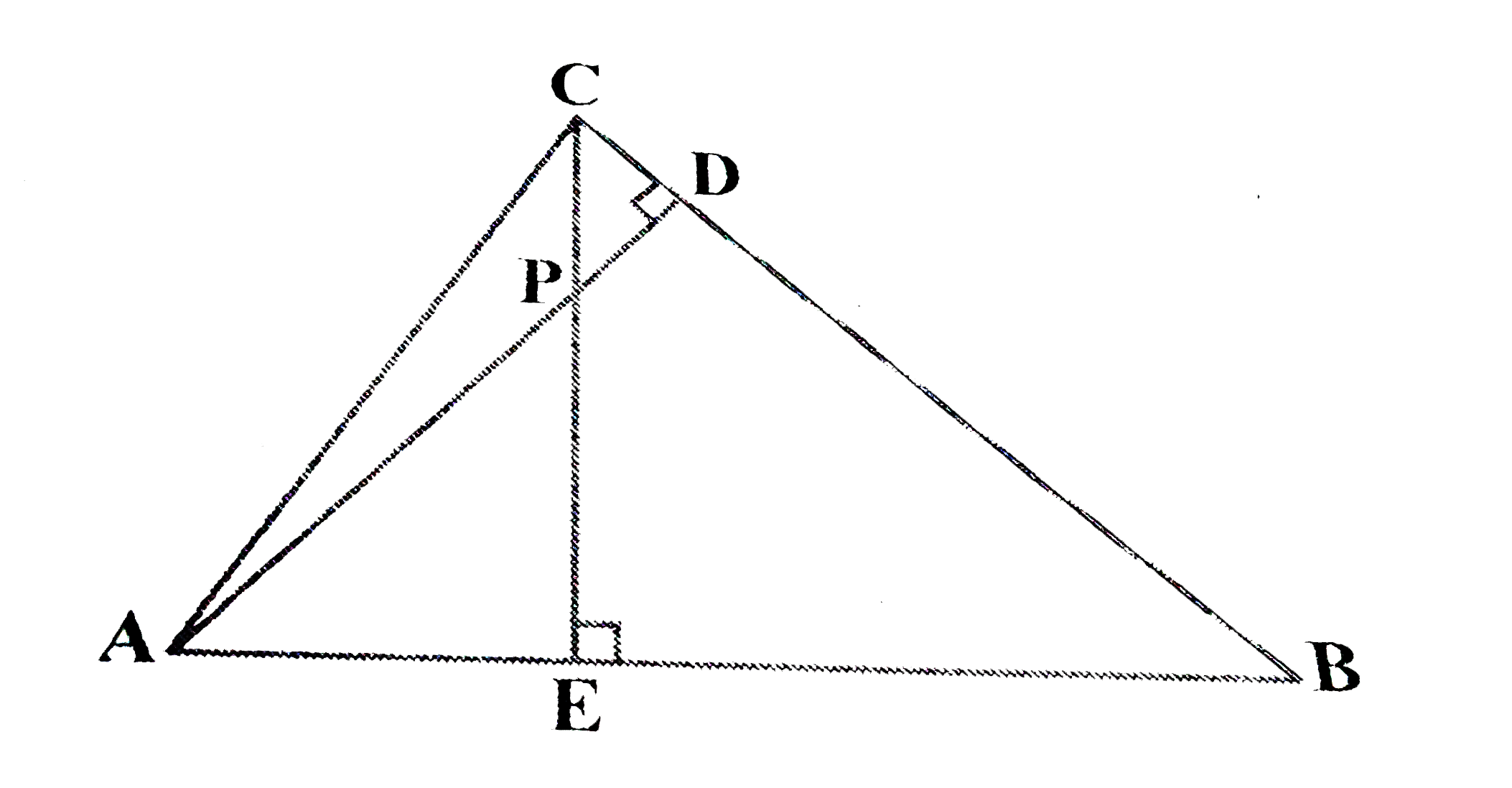
View SolutionIn Figure ABDC and ADBC. Prove that ∠DAB= ∠DCB
View SolutionIn ΔABC, if a=18, b=24 and c=30 and ∠C=900 find sinA, sinB and sinC.
View SolutionIn a ΔABC prove that cos(A+B)+cosC=0.
View SolutionIn Figure, ABC and DBC are two triangles on the same base BC such that AB=AC and DB=DC. Prove that ∠ABD=∠ACD
View SolutionIn Figure, it is given that AB=CD and AD=BC. Prove that ADC ≅CBA.
View SolutionIn a ΔABC, if b=√3, c=1 and ∠A=300, then find a
View Solution
