In the given AB=BC=DCand∠AOB=50∘
∠AOC
The correct Answer is:100∘
To solve the problem, we need to find the measure of angle AOC given that AB = BC = DC and angle AOB = 50°.
1. Identify Given Information:
- We have three equal sides: AB = BC = DC.
- Angle AOB = 50°.
2. Use Properties of Isosceles Triangles:
- Since AB = BC, triangle AOB is isosceles. Therefore, the angles opposite to equal sides are also equal.
- This means angle AOB = angle BOC = angle COD.
3. Set Up the Equal Angles:
- Let angle BOC = angle COD = x.
- We know angle AOB = 50°, so we can write:
- angle AOB = 50°,
- angle BOC = x,
- angle COD = x.
4. Sum of Angles Around Point O:
- The sum of angles around point O must equal 360°:
- angle AOB + angle BOC + angle COD = 360°.
- Substitute the known values:
- 50° + x + x = 360°.
5. Solve for x:
- Combine like terms:
- 50° + 2x = 360°.
- Subtract 50° from both sides:
- 2x = 310°.
- Divide by 2:
- x = 155°.
6. Find Angle AOC:
- Angle AOC is the sum of angle AOB and angle BOC:
- angle AOC = angle AOB + angle BOC = 50° + 155°.
- Therefore, angle AOC = 205°.
Final Answer:
Angle AOC = 205°.
---
- We have three equal sides: AB = BC = DC.
- Angle AOB = 50°.
- Since AB = BC, triangle AOB is isosceles. Therefore, the angles opposite to equal sides are also equal.
- This means angle AOB = angle BOC = angle COD.
- Let angle BOC = angle COD = x.
- We know angle AOB = 50°, so we can write:
- angle AOB = 50°,
- angle BOC = x,
- angle COD = x.
- The sum of angles around point O must equal 360°:
- angle AOB + angle BOC + angle COD = 360°.
- Substitute the known values:
- 50° + x + x = 360°.
- Combine like terms:
- 50° + 2x = 360°.
- Subtract 50° from both sides:
- 2x = 310°.
- Divide by 2:
- x = 155°.
- Angle AOC is the sum of angle AOB and angle BOC:
- angle AOC = angle AOB + angle BOC = 50° + 155°.
- Therefore, angle AOC = 205°.
Angle AOC = 205°.
Topper's Solved these Questions
Similar Questions
In the given AB=BC=DCand∠AOB=50∘
∠AOD
View SolutionIn the given AB=BC=DCand∠AOB=50∘
∠BOD
View SolutionIn the given figure, AB = BC = DC and ∠AOB=50∘

∠AOC =?
View SolutionIn the given arc AB= twice are BC and ∠AOB=80∘ find:
∠BOC
View SolutionIn the given arc AB= twice are BC and ∠AOB=80∘ find:
∠OAC
View SolutionIn the given figure, AC = AE, AB = AD and ∠BAD=∠EAC. Show that : BC = DE.

View SolutionA circle, with centre O, circumscribs a pentagon ABCDE. IF AB−BC=CDand∠BCD=126∘, find:
∠AOC
View SolutionIn the given figure if find, ∠AOC=45∘, find ∠BOD
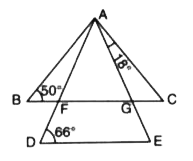
View SolutionIn the following figure , AB = BC and AD = DE.
if ∠B=50∘,∠D=66∘and∠GAC=18∘ find the measure of angles DAE, BAF and AGF.
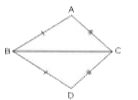
View SolutionIn the given figure, AB = DB and AC = DC. If ∠ABD=58∘,∠DBC=(2x−4)∘,∠ACB=y+15∘and∠DCB=63∘, find the values of x and y.
View Solution
