In the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔABC is right angled isosceles triangle whose hypotenuse AC=4√2 units.
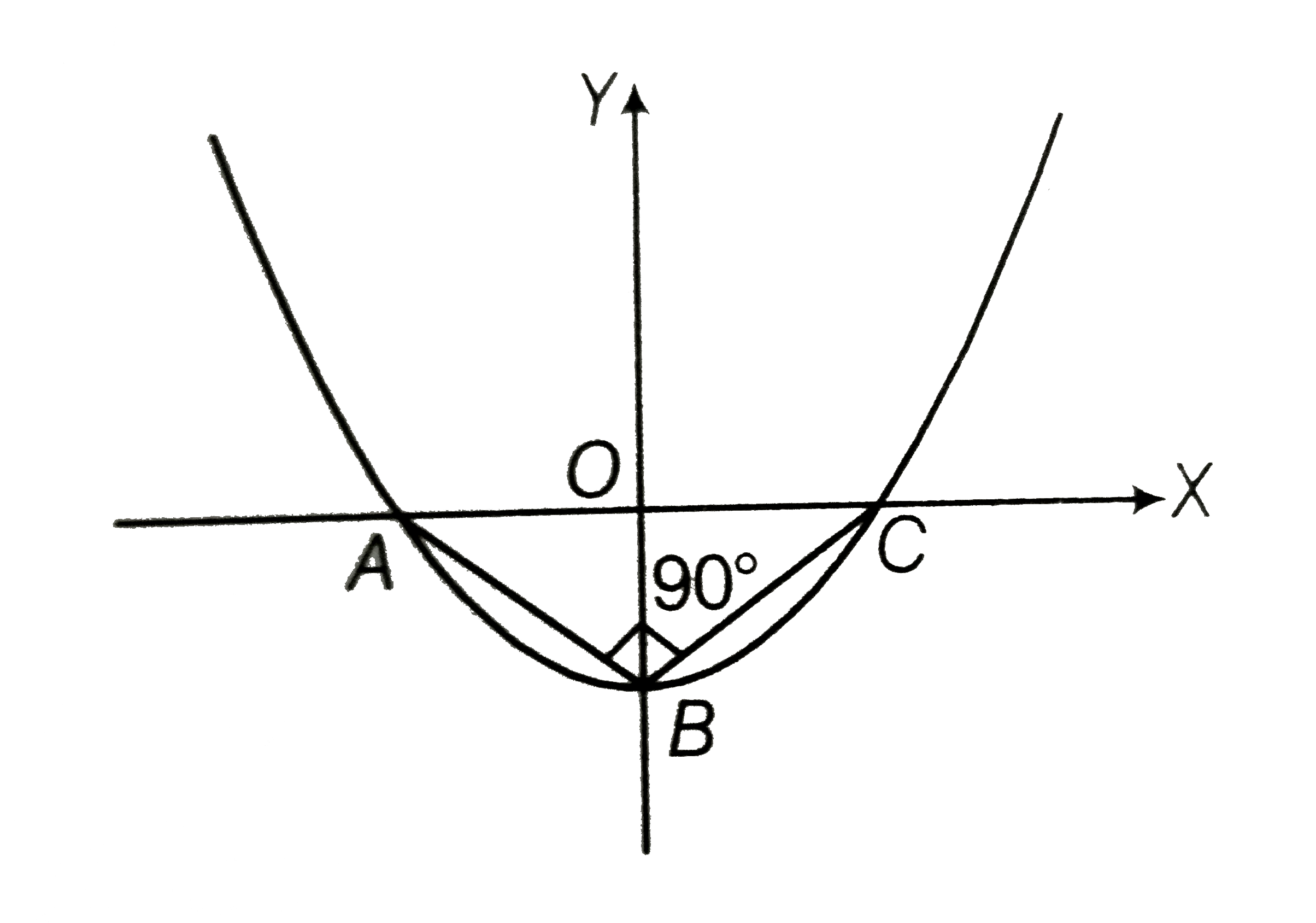
y=f(x) is given by Solution in Punjabi
y=−x2−8
y=x22√2−2√2
y=x2−4
y=x22−√2
The correct Answer is:B
Given that AC=4√2 units
∴AB=BC=AC√2=4 units andd OB=√(BC)2−(OC)2
=√(4)2−(2√2)2[∵OC=AC2]
=2√2 units
∴ Vertices are A=(−2√2,0),
B=−(0,−2√2)
and C=(2√2,0)
Since y=f(x)=ax2+bx+c passes through A,B and C then
0=8a−2√2b+c−2√2=c
and 0=8a+2√2b+c
We get b=0,a=12√20 and c=−2√2
∴y=f(x)=x22√2−2√2
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Single Integer Answer Type Questions)
10 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Matching Type Questions)
2 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - The Straight Lines Exercise 8 : (Questions Asked in Previous 13 years Exams)
1 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam
2 Videos
Similar Questions
The sum of all the real roots of the equation |x−2|2+|x−2|−2=0 is
View SolutionColumn I contain rational algebraic expressions and ColumnII contains possible integers which lie in their range. Match the entries of Column I with one or more entries of the elements of Column II.

View SolutionIf 0<a<b<c and the roots α,β of the equation ax2+bx+c=0 are non-real complex numbers, then
View SolutionSolve the following system of inequalities graphically
x+5y≤25,2x+2y≥2,2x−2y≤0,x≥0,y≥0
View SolutionConsider the line L1:x−12=y−1=z+31,L2:x−41=y+31=z+32 find the angle between them.
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.
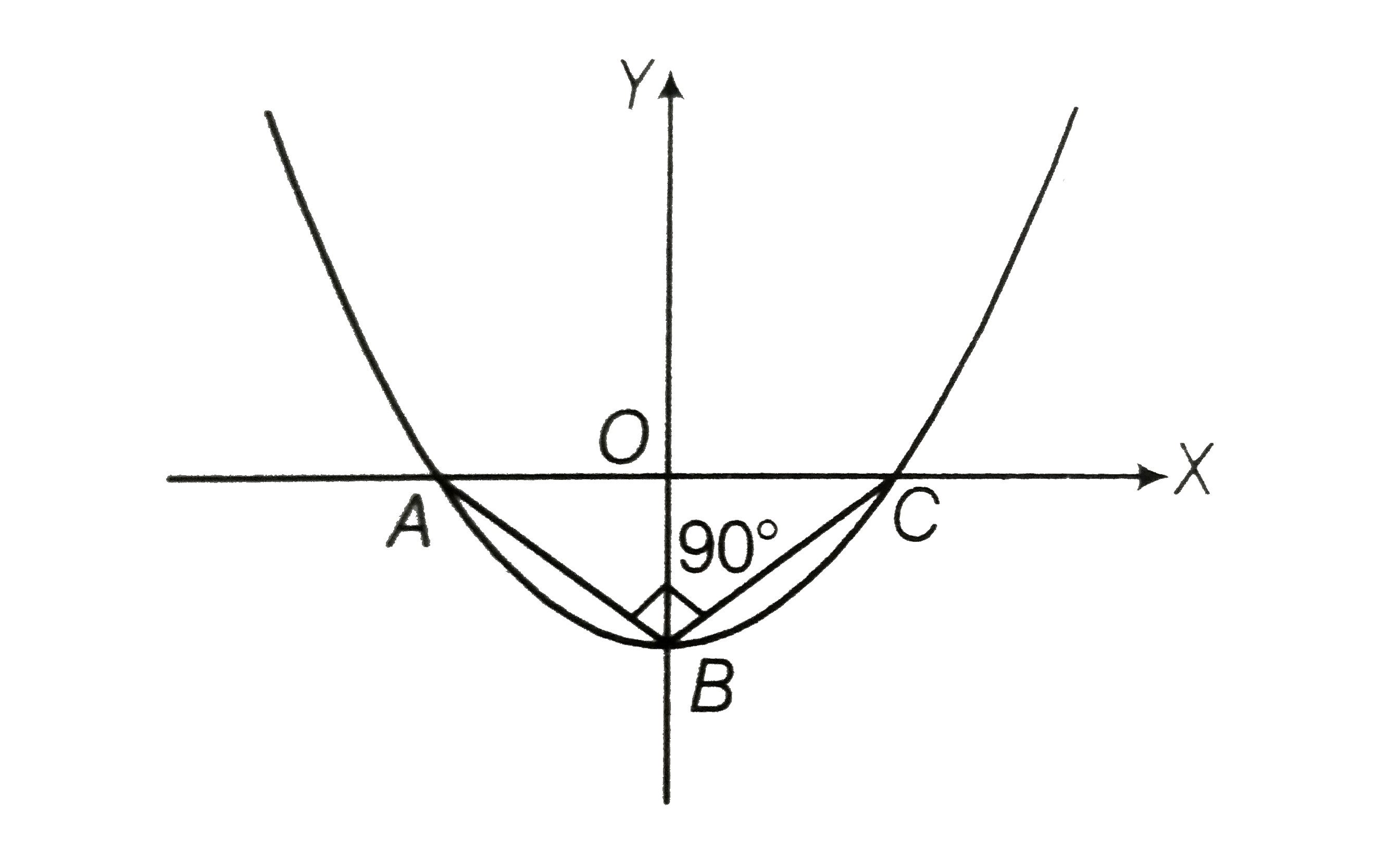
Minimum valueof y=f(x) is
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.
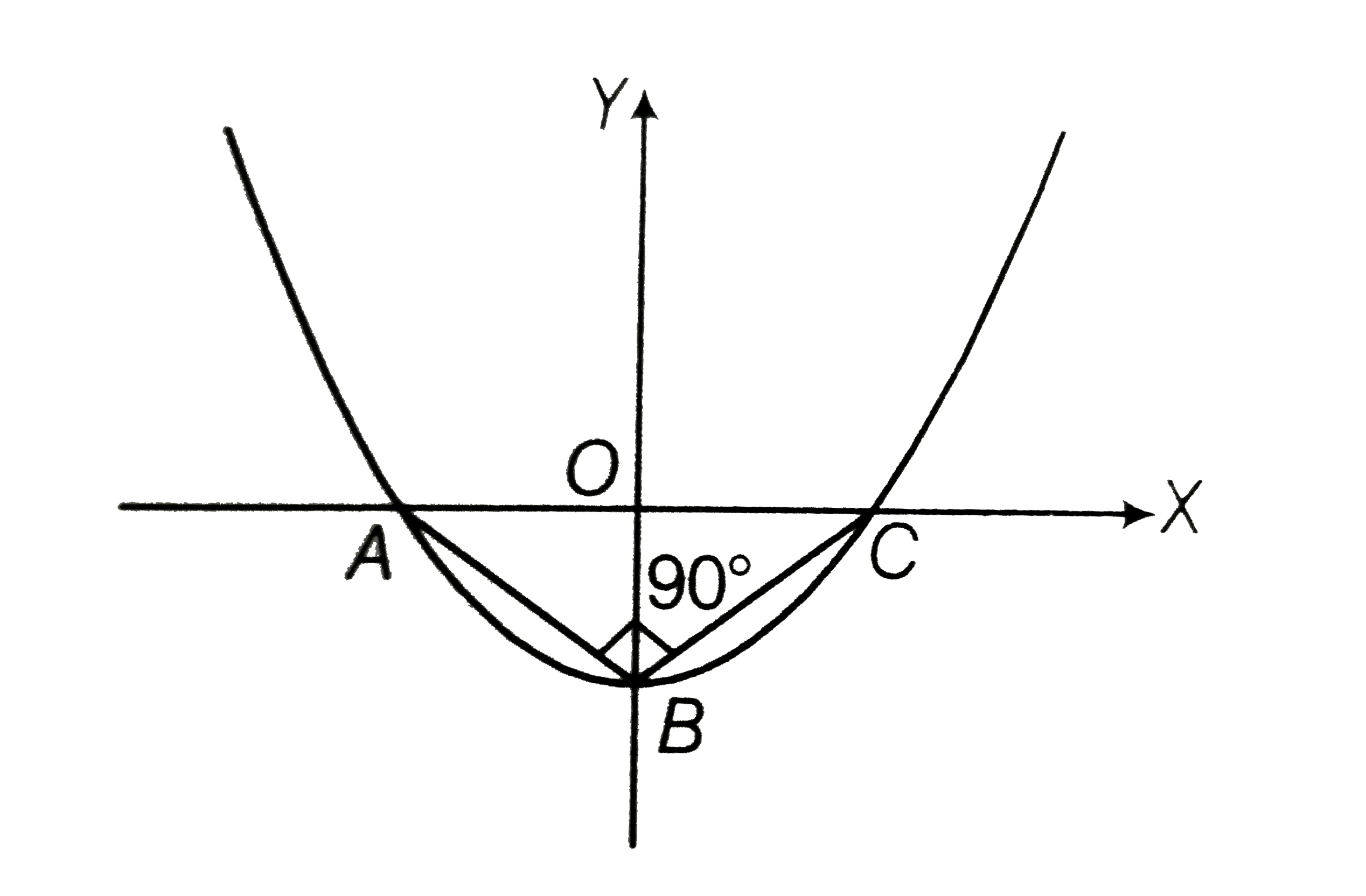
Number of integral value of λ for which λ2 lies between the roots of f(x)=0, is
View Solutionदिये गये चित्र में ΔABC के शीर्ष y=f(x)=ax2+bx+c पर स्थित है ΔABC समकोण समद्विबाहु त्रिभुज है जिसका कर्ण AC=4√2 इकाई है, तब

y=f(x) दिया गया है
View Solutionदिये गये चित्र में ΔABC के शीर्ष y=f(x)=ax2+bx+c पर स्थित है ΔABC समकोण समद्विबाहु त्रिभुज है जिसका कर्ण AC=4√2 इकाई है, तब
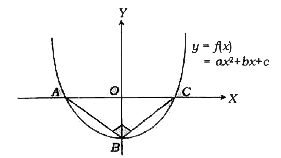
समीकरण y=f(x) का न्यूनतम मान है
View Solution
