In the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.
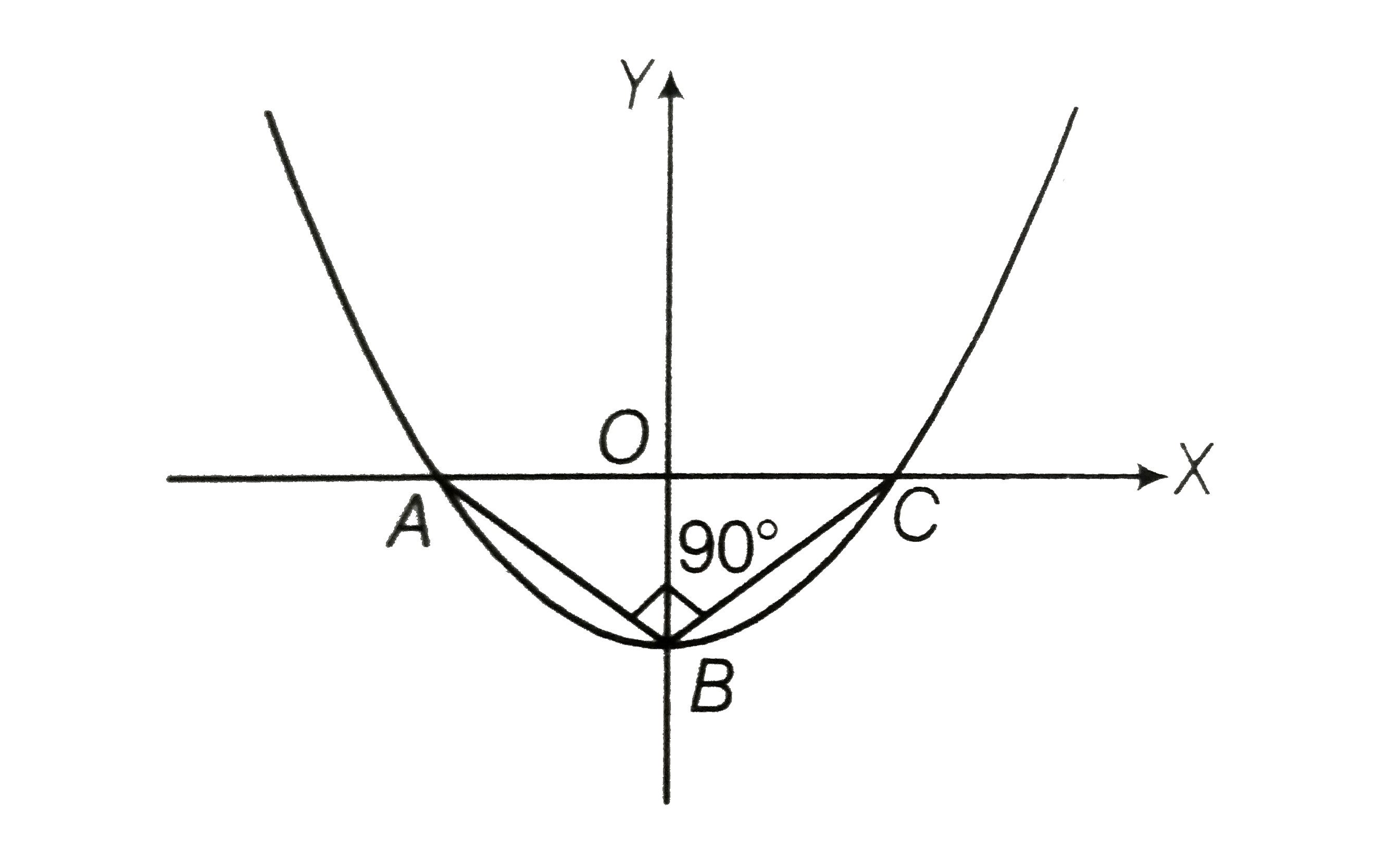
Minimum valueof y=f(x) is Solution in Gujrati
−4√2
−2√2
0
2√2
The correct Answer is:B
Given that AC=4√2 units
∴AB=BC=AC√2=4 units andd OB=√(BC)2−(OC)2
=√(4)2−(2√2)2[∵OC=AC2]
=2√2 units
∴ Vertices are A=(−2√2,0),
B=−(0,−2√2)
and C=(2√2,0)
Minimum value of y=x22√2−2√2 is at x=0
∴(y)min=−2√2
Similar Questions
In the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.
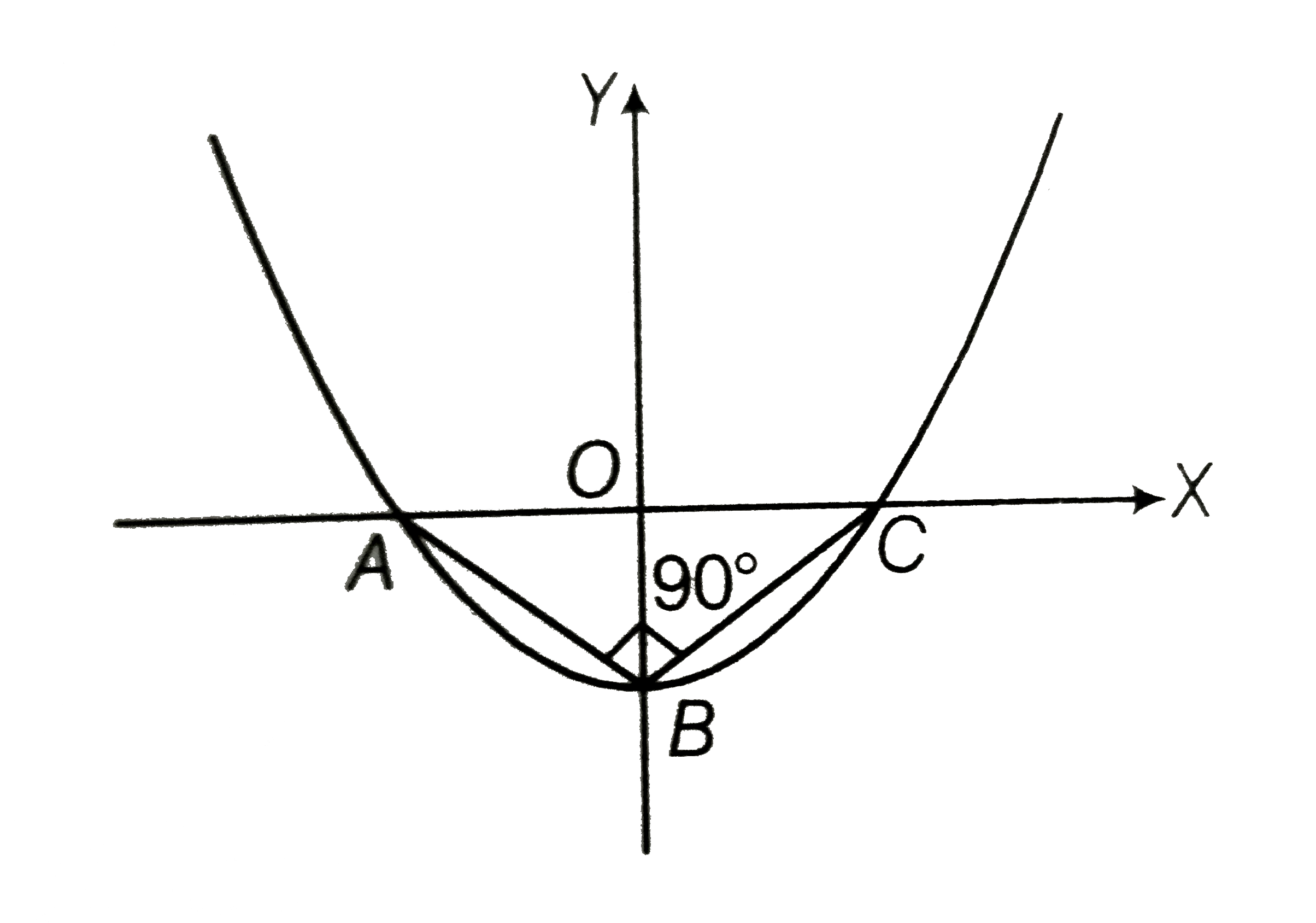
y=f(x) is given by
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.
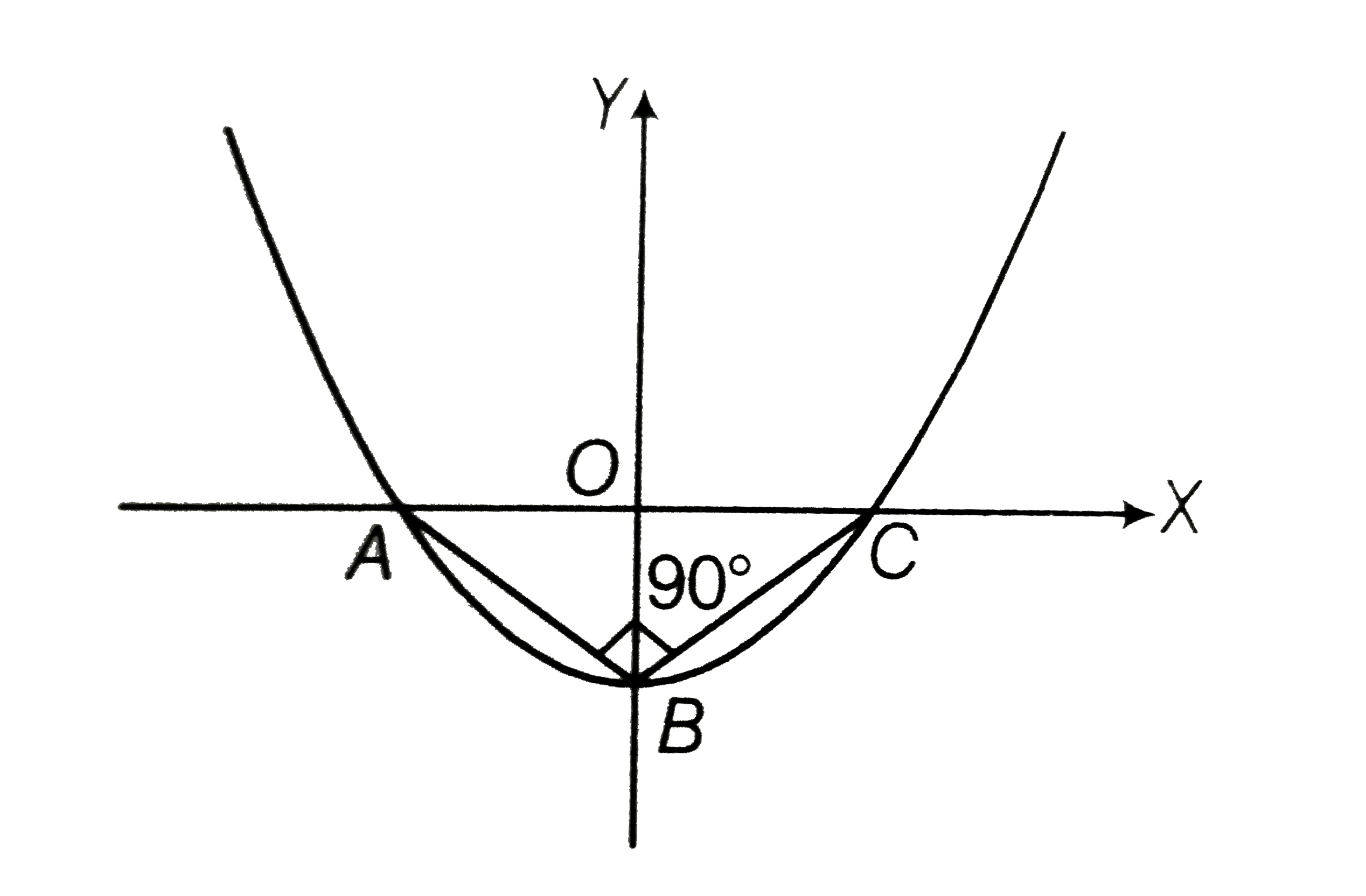
Number of integral value of λ for which λ2 lies between the roots of f(x)=0, is
View Solutionदिये गये चित्र में ΔABC के शीर्ष y=f(x)=ax2+bx+c पर स्थित है ΔABC समकोण समद्विबाहु त्रिभुज है जिसका कर्ण AC=4√2 इकाई है, तब

y=f(x) दिया गया है
View Solutionदिये गये चित्र में ΔABC के शीर्ष y=f(x)=ax2+bx+c पर स्थित है ΔABC समकोण समद्विबाहु त्रिभुज है जिसका कर्ण AC=4√2 इकाई है, तब
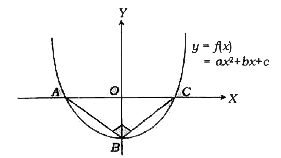
समीकरण y=f(x) का न्यूनतम मान है
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔABC is right angled isosceles triangle whose hypotenuse AC=4√2 units.

y=f(x) is given by
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.

Number of integral value of λ for which λ2 lies between the roots of f(x)=0, is
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.

y=f(x) is given by
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.

Number of integral value of λ for which λ2 lies between the roots of f(x)=0, is
View Solution
