In the given figure, AB and AC are tangents to the circle with centre O such that ∠BAC=40∘. Then , ∠BOC is equal to

A
80∘
B
100∘
C
120∘
D
140∘
Video Solution
Text Solution
ABOC is a cyclic quadrilateral
∴∠BAC+∠BOC=180∘⇒∠BOC=180∘−∠BAC=180∘−40∘=140∘
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Assertion-and-Reason1videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Test Yourself20videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Multiple Choice Questions (Mcq)15videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)30videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself10videos
CONSTRUCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
AB and AC are tangents to the circle with centre O. Then x equals.
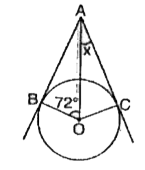 A22∘B18∘C20∘D36∘
A22∘B18∘C20∘D36∘ - Question 2 - Select One
In the given figure, if PA and PB are tangents to the circle with centre O such that ∠APB=54∘, then ∠ OAB equals
A36∘B18∘C27∘D36∘ - Question 3 - Select One
In the given figure, AB and AC are tangents to the circle with centre O. Given that ∠BAC=70∘ and P is a point on the minor are BC, find ∠ BPC.
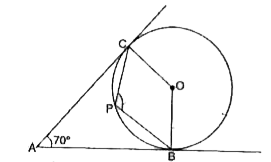 A110∘B140∘C125∘D136∘
A110∘B140∘C125∘D136∘
In the given figure,AB and BC are two chords of the circle with Centre O ,where ∠BAO=50∘,∠BCO=35∘,then ∠AOC is equal to
View SolutionIn the given figure , if TP and TQ are the two tangents to a circle with centre O so that ∠POQ=110∘ , then ∠PTQ is equal to
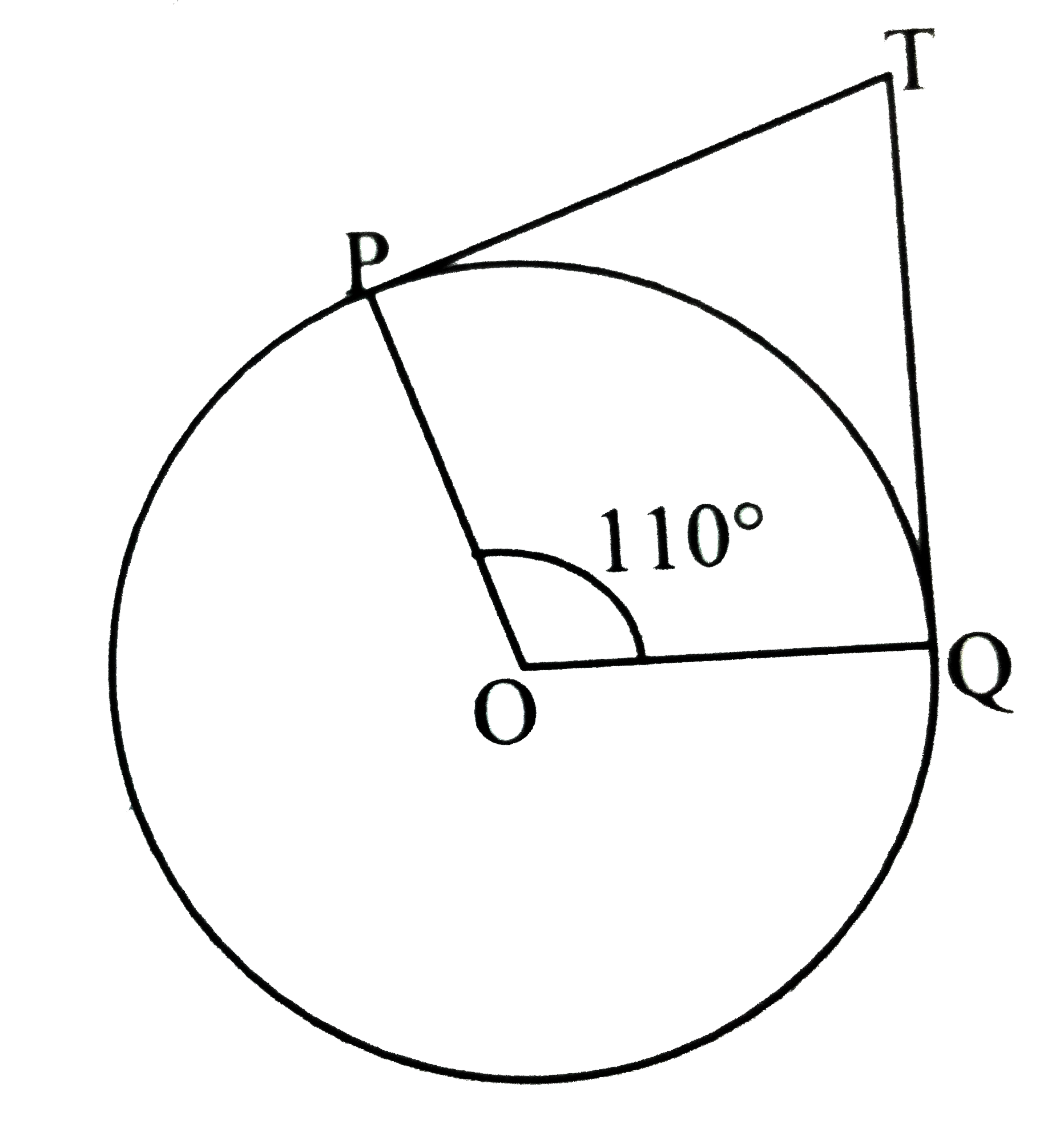 View Solution
View SolutionIn the given figure, AB is a tangent to a circle with centre O. Prove ∠BPQ=∠PRQ.
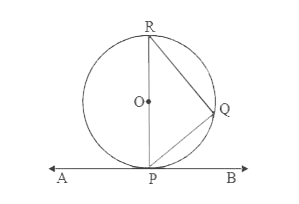 View Solution
View SolutionIn Figure, two tangents ABandAC are drawn to a circle with centre O such that ∠BAC=1200. Prove that OA=2AB
View SolutionIn the given figure , AB is a tangent to the circle with centre O and ∠BPQ=40∘ . Find PQ : AQ.
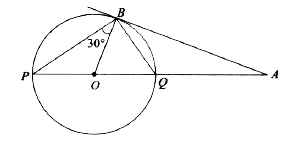 View Solution
View Solution