In the given figure, PQ is a tangent to a circle with centre O. A is the point of contact. If ∠PAB=67∘, then the measure of ∠AQB is

73∘
64∘
53∘
44∘
∠BAC=90∘ [angle in a semicircle]
∠PAB+∠BAC+∠CAQ=180∘⇒∠CAQ=180∘−(90∘+67∘)=23∘.
∠ACB=∠PAB=67∘ [angle in alternate segments]
∠ACB+∠ACQ=180∘ [linear pair]
⇒∠ACQ=180∘−67∘=113∘.
Now, ∠CAQ+∠ACQ+∠AQC=180∘ [in ΔACQ]
⇒∠AQC=180∘−(23∘+113∘)=44∘⇒∠AQB=44∘.
Topper's Solved these Questions
- CIRCLESBook:RS AGGARWALChapter:CIRCLESExercise:Assertion-and-Reason
Explore 1 Video
- CIRCLESBook:RS AGGARWALChapter:CIRCLESExercise:Test Yourself
Explore 20 Videos
- CIRCLESBook:RS AGGARWALChapter:CIRCLESExercise:Multiple Choice Questions (Mcq)
Explore 15 Videos
- ARITHMETIC PROGRESSIONBook:RS AGGARWALChapter:ARITHMETIC PROGRESSIONExercise:Multiple Choice Questions (Mcq)
Explore 30 Videos
- CONSTRUCTIONSBook:RS AGGARWALChapter:CONSTRUCTIONSExercise:Test Yourself
Explore 10 Videos
Similar Questions
Knowledge Check
In figure , APB is a tangent to a circle with centre O at point, If ∠QPB=50∘ , then the measure of ∠POQ is
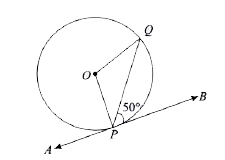 A100∘B120∘C140∘D150∘
A100∘B120∘C140∘D150∘In the given figure , AB is a tangent to the circle with centre O and ∠BPQ=40∘ . Find PQ : AQ.
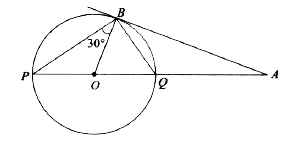 A1:2B1:3C2:1D3:1
A1:2B1:3C2:1D3:1
In figure-3, PQ is tangent to the circle with centre at O, at the point B. if ∠AOB=100∘, then ∠ABP is equal to
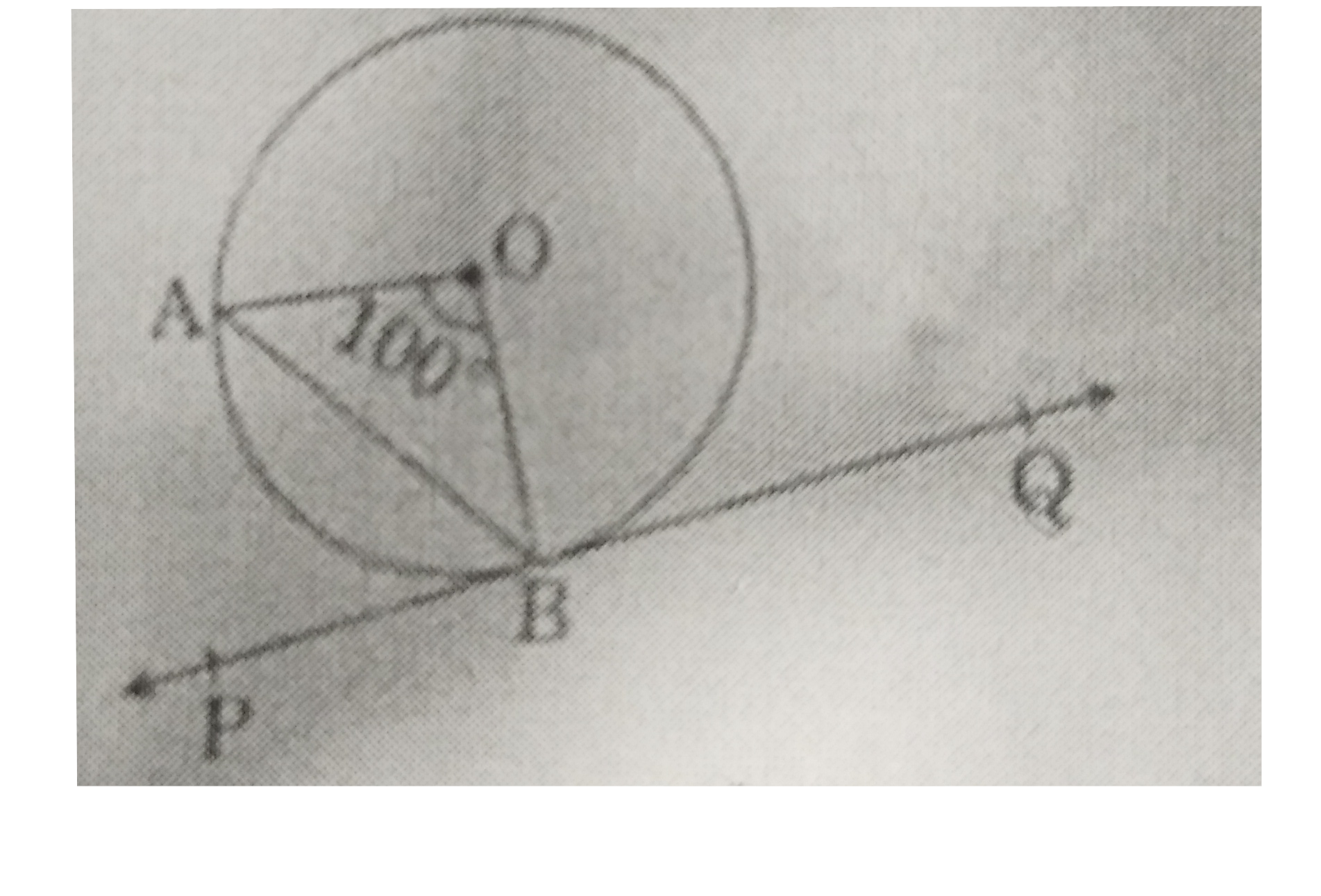
View SolutionIn figure PQ is tangent to the circle with centre at O at the point B , if ∠AOB=100∘, then ∠ABP is equal to

View SolutionIn the figure, PQ is tangent to a circle with centre O. OQ=12, PQ=6. Find the area of the shaded portion

View SolutionIn the given figure, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT=60∘ find ∠PRQ
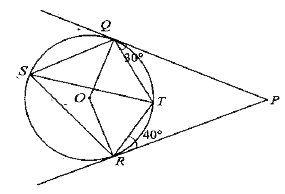
View SolutionIn the figures, PQ and PR are tangents to the circle with centre O. Find RSQ , RTQ , and RˆPQ
View SolutionIn the figure, PA and PB are tangents to the circle with centre O such that ∠APB=50∘, and the measure of ∠OAB is …………
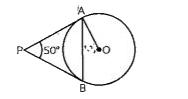
View Solution