In the given figure, O is the centre of the circle. AB is the tangent to the circle at the point P. If ∠PAO=30∘ then ∠CPB+∠ACP is equal to

A
60∘
B
90∘
C
120∘
D
150∘
Video Solution
Text Solution
∠DPC=90∘ [angle in semicircle]
and ∠DPA=∠DCP [angles in alternate segments]
Now, ∠CPB+∠DPA+∠DPC=180∘
⇒∠CPB+∠DPA=90∘⇒∠CPB+∠DCP=90∘
⇒∠CPB+∠ACP=90∘
|
Topper's Solved these Questions
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Assertion-and-Reason
1 Video
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Test Yourself
20 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Multiple Choice Questions (Mcq)
15 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos
Similar Questions
Knowledge Check
In the given figure , O is the centre of the circle . AP and AQ are tangents to the circle .∠PRQ=
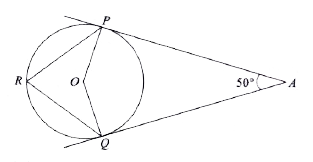 A55∘B45∘C75∘D65∘
A55∘B45∘C75∘D65∘In the given figure, O is the centre of the circle. AB is tangent. AB=12cmandOB=13cm. Find OA:
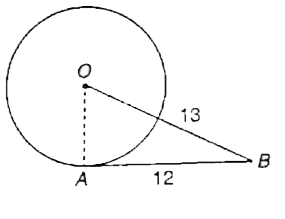 A6.5 cmB6 cmC5 cmDnone of these
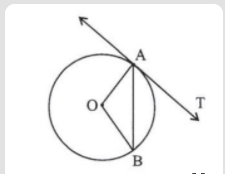
A6.5 cmB6 cmC5 cmDnone of theseIn the given figure, O is the centre of a circle , AB is a chord and AT is the tangent at A. If ∠AOB=100∘ then ∠BAT is equal to
A40∘B50∘C90∘D100∘
In the figure,O is the centre of the circle PQ is the tangent at point P then what is the measure of ∠OPQ ?Why ?

View SolutionIn the figure , point P is the centre of the circle and AB is the diameter . The co-ordinates of A are
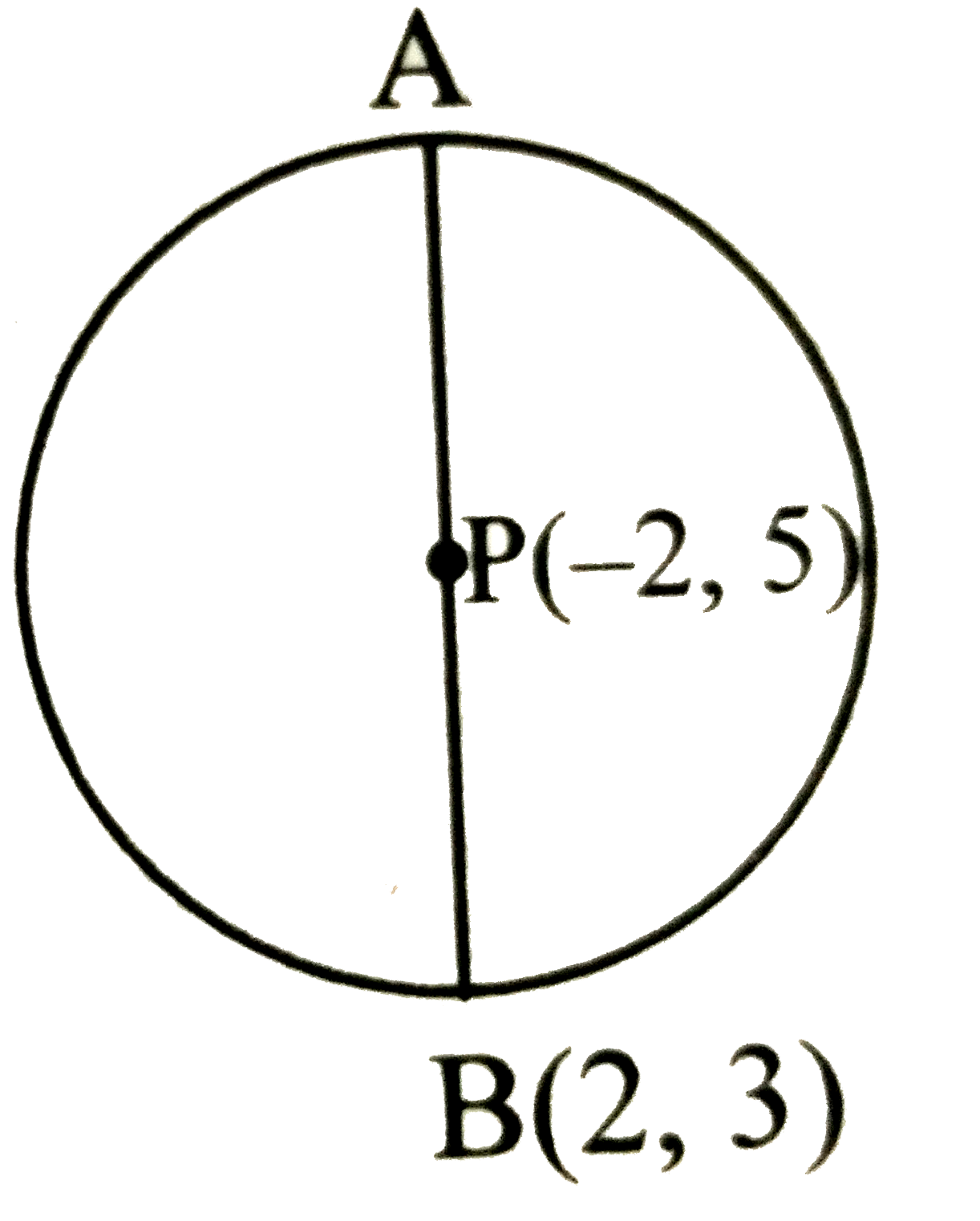
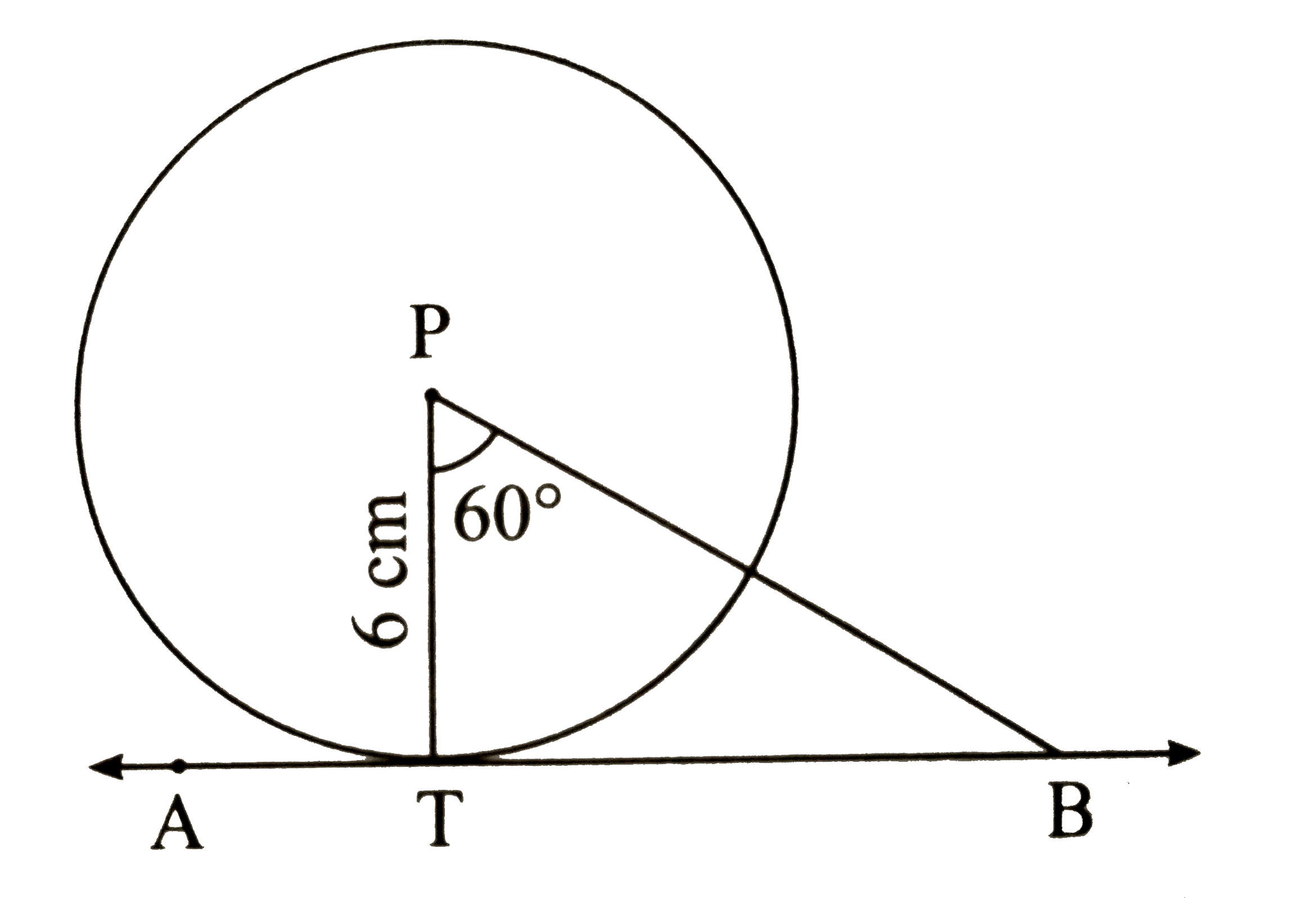
View SolutionIn the figure, point P is the centre of the circle and line AB is the tangent to the circle at the point T. The radius of the circle is 6 cm . Find PB, if ∠TPB=60∘
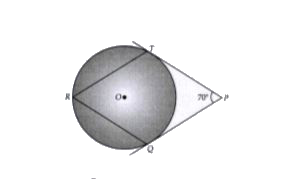
View SolutionIn figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ=70∘, find ∠TRQ.
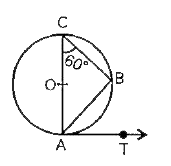
View SolutionIn the figure, O is the centre of a circle and AT is a tangent at point A. The measure of ∠BAT is:
View Solution