In the given figure, ABCD is a parallelogram BC is produced to point X. prove that :
area(ΔABX)=area( .ACXD)
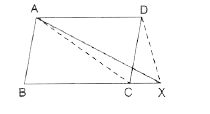
Step by step video & image solution for In the given figure, ABCD is a parallelogram BC is produced to point X. prove that : "area" (DeltaABX)= "area" (quad.ACXD) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(B)
16 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
Similar Questions
In the given figure ABCD is a parallelogram. Prove that AB = 2BC.

View SolutionIn the given figure, ABCD is a parallelogram. Find the area of ΔAED

View SolutionIn the figure, the area of parallelogram ABCD is

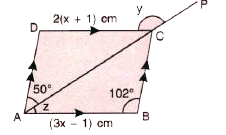
View SolutionIn the given figure, ABCD is a parallelogram. Find the values of x, y and z
View SolutionIn the adjoning figure, ABCD is a parallelogram. Prove that : area of ΔBPC= area of ΔDPQ

View SolutionIn the given figure, ABCD is a parallelogram whose area is 60cm2. Find the area of ΔACB
View SolutionA point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar(ΔADF)=ar(ABFC).
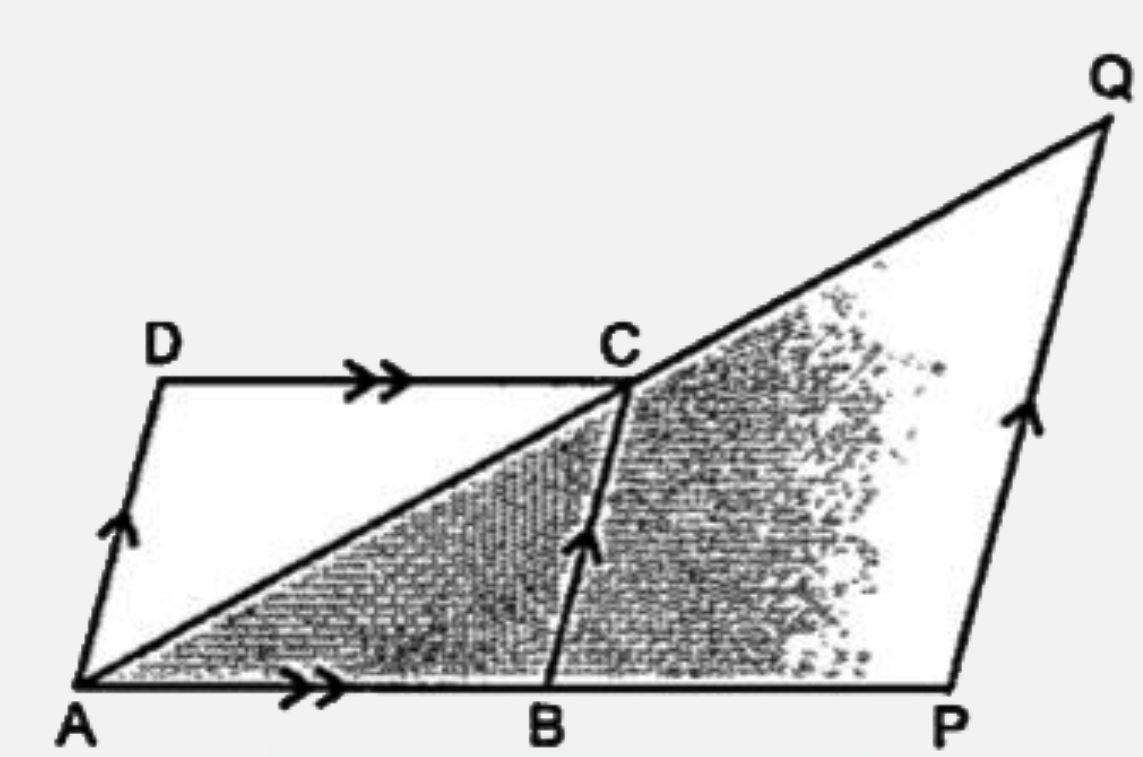
View SolutionIn the given figure, ABCD is a parallelogram. AB is produced to P, such that AB=BPandPQ is drawn parallel to BC to meet AC produced at Q. Given AB=8cm,AD=5cm,AC=10cm.
Prove that point C is mid-point of AQ.
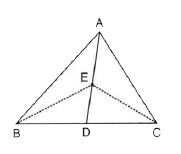
View SolutionIn the given figure, AD is median of ΔABC and E is any point on median AD. Prove that Area (ΔABE) = Area (ΔACE)
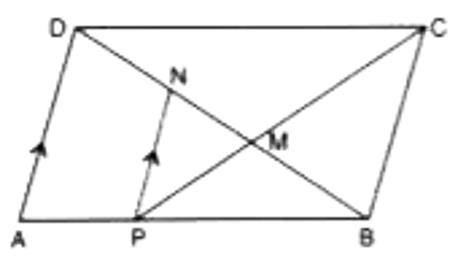
View SolutionIn the given figure, ABCD is a parallelogram and AP:PB=3:5. Calculate:
(i)area (ΔPBN): area (trapezium APND)
(ii) PN:BCand area (ΔPMN): area (ΔBMC)
View Solution
