A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar(ΔADF)=ar(ABFC).
To prove that the area of triangle ADF is equal to the area of quadrilateral ABFC, we will follow these steps:
1. Identify the Parallelogram and the Triangles:
We have a parallelogram ABCD with point E on side BC. Lines AE and DC are extended to meet at point F.
2. Use the Property of Diagonals:
The diagonal AC divides the parallelogram ABCD into two congruent triangles:
Area of △ABC=Area of △ADC
Let's denote this area as S. Therefore, we can write:
Area of △ABC=SandArea of △ADC=S
(Equation 1)
3. Relate Triangle ABF to Triangle ABC:
Triangles ABF and ABC share the same base AB and are between the same parallel lines (AB and DC). Thus, we can say:
Area of △ABF=Area of △ABC
Therefore, we have:
Area of △ABF=S(Equation 2)
4. Compare the Areas:
From Equations 1 and 2, we can conclude:
Area of △ADC=Area of △ABF
5. Add Area of Triangle ACF:
Now, we add the area of triangle ACF to both sides:
Area of △ADC+Area of △ACF=Area of △ABF+Area of △ACF
This gives us:
Area of △ADF=Area of △ABF+Area of △ACF
6. Recognize the Quadrilateral:
The right-hand side can be recognized as the area of quadrilateral ABFC:
Area of △ADF=Area of ABFC
7. Conclusion:
Thus, we have proved that:
Area of △ADF=Area of ABFC
We have a parallelogram ABCD with point E on side BC. Lines AE and DC are extended to meet at point F.
The diagonal AC divides the parallelogram ABCD into two congruent triangles:
Area of △ABC=Area of △ADC
Let's denote this area as S. Therefore, we can write:
Area of △ABC=SandArea of △ADC=S
(Equation 1)
Triangles ABF and ABC share the same base AB and are between the same parallel lines (AB and DC). Thus, we can say:
Area of △ABF=Area of △ABC
Therefore, we have:
Area of △ABF=S(Equation 2)
From Equations 1 and 2, we can conclude:
Area of △ADC=Area of △ABF
Now, we add the area of triangle ACF to both sides:
Area of △ADC+Area of △ACF=Area of △ABF+Area of △ACF
This gives us:
Area of △ADF=Area of △ABF+Area of △ACF
The right-hand side can be recognized as the area of quadrilateral ABFC:
Area of △ADF=Area of ABFC
Thus, we have proved that:
Area of △ADF=Area of ABFC
Topper's Solved these Questions
Similar Questions
Any point D is taken on the side BC of a ΔABC and AD is produced to E such that AD = DE , prove that area of ΔBCE= area of ΔABC,
View SolutionA circle intersects the side AD of a parallelogram ABCD at P and BC produced at Q. Prove that square PDQC is cyclic .
View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE~ΔCFB .
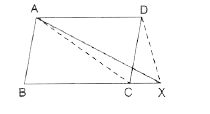
View SolutionIn the given figure, ABCD is a parallelogram BC is produced to point X. prove that :
area(ΔABX)=area( .ACXD)
View SolutionP is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that :
DL:DP=AL:DC
View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE~ΔCFB.
View SolutionP is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that :
DP:PL=DC:BL.
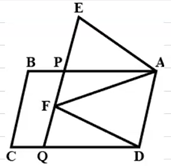
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
View SolutionIf E is a point on side AD produced of a parallelogram ABCD and BE intersects CD at F , Prove that △ABE~△CFB .
View SolutionP is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
View Solution