In the given figure, ∠ACB=90∘andCD⊥AB. Prove that CD2=BD⋅AD

Video Solution
Text Solution
GIVEN AΔABC in which ∠ACB=90∘andCD⊥AB.
TO RPOOVE CD2=BD⋅AD.
PROOF In right ΔADC, we get have ∠1+∠2=90∘
In right ΔACB, we have
∠1+∠3=90∘
∴∠1+∠2=∠1+∠3⇒∠=2∠3.
In ΔABCandΔCDB, we have
∠2=∠3
and∠ADC=∠CDB=90∘
∴ΔADC~ΔCDB=90∘
∴ADCD=CDBD
Hence, CD2=BD⋅AD.
|
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:SOLVED EXAMPLE
Explore 4 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:EXERCISE 7 A
Explore 1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
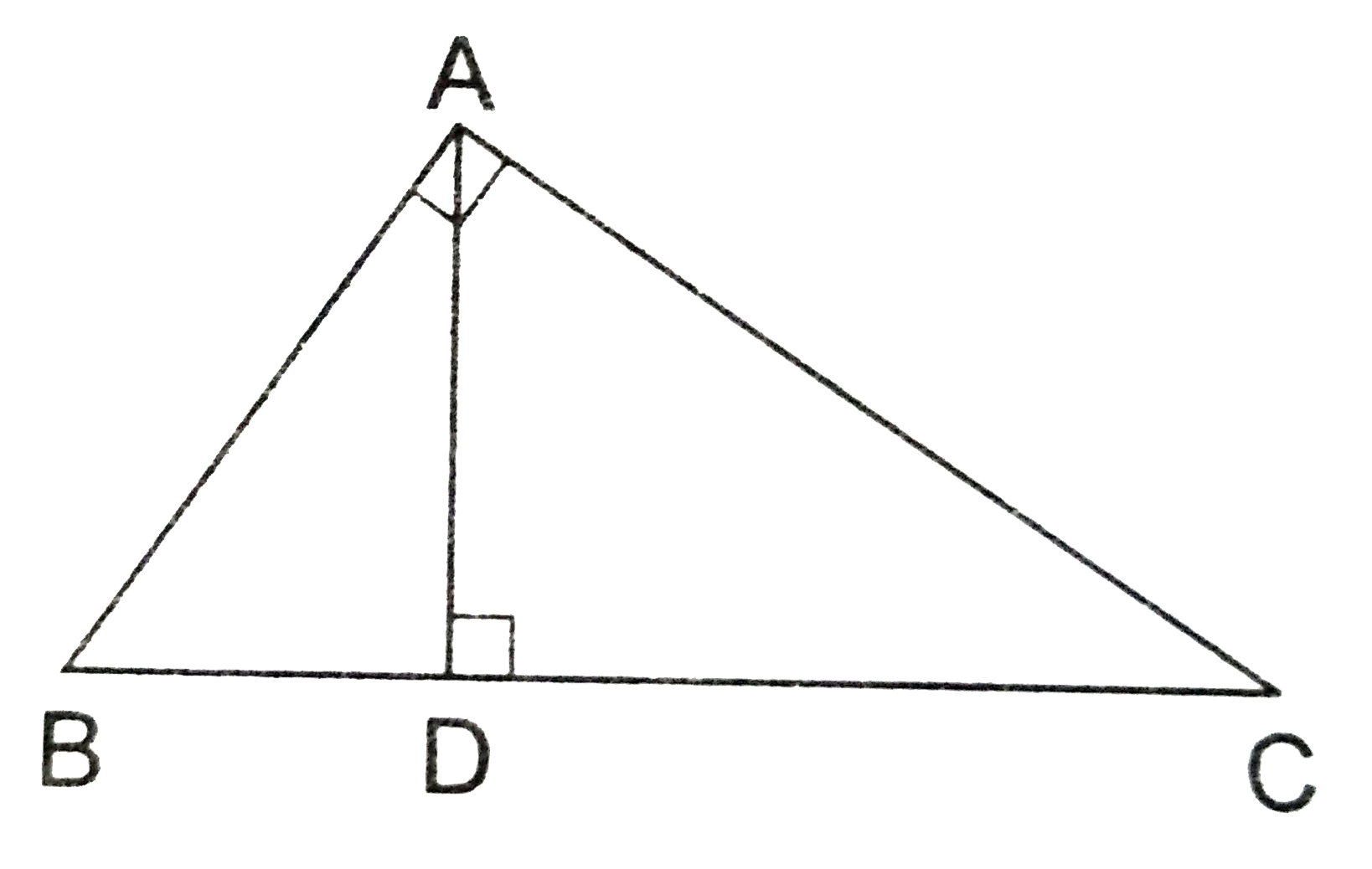
In the given figure, ∠BAC=90∘andAD⊥BC.then,
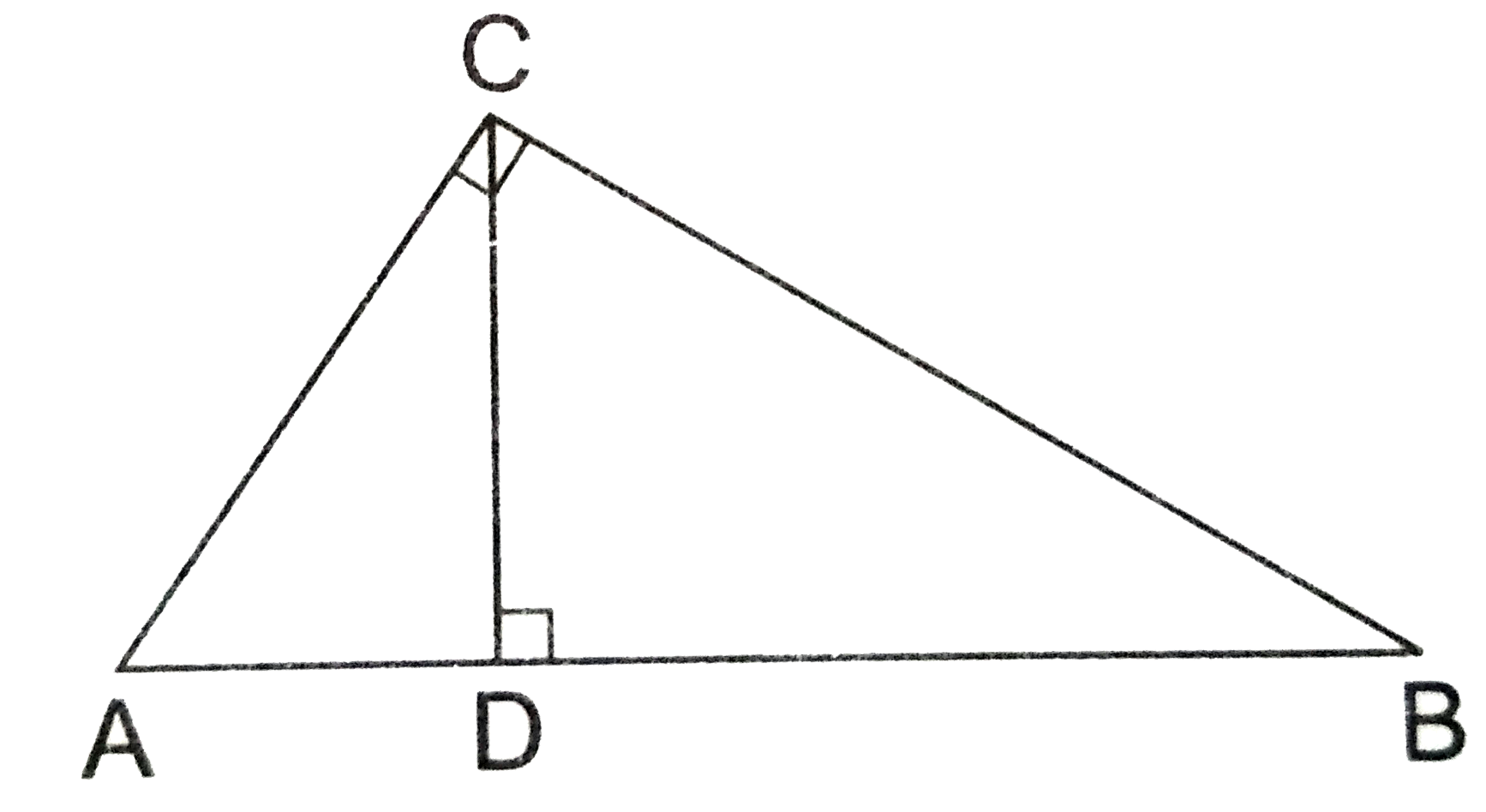
View SolutionIn the given figure ∠ABC=90∘andCD⊥AB. Prove that BC2AC2=BDAD
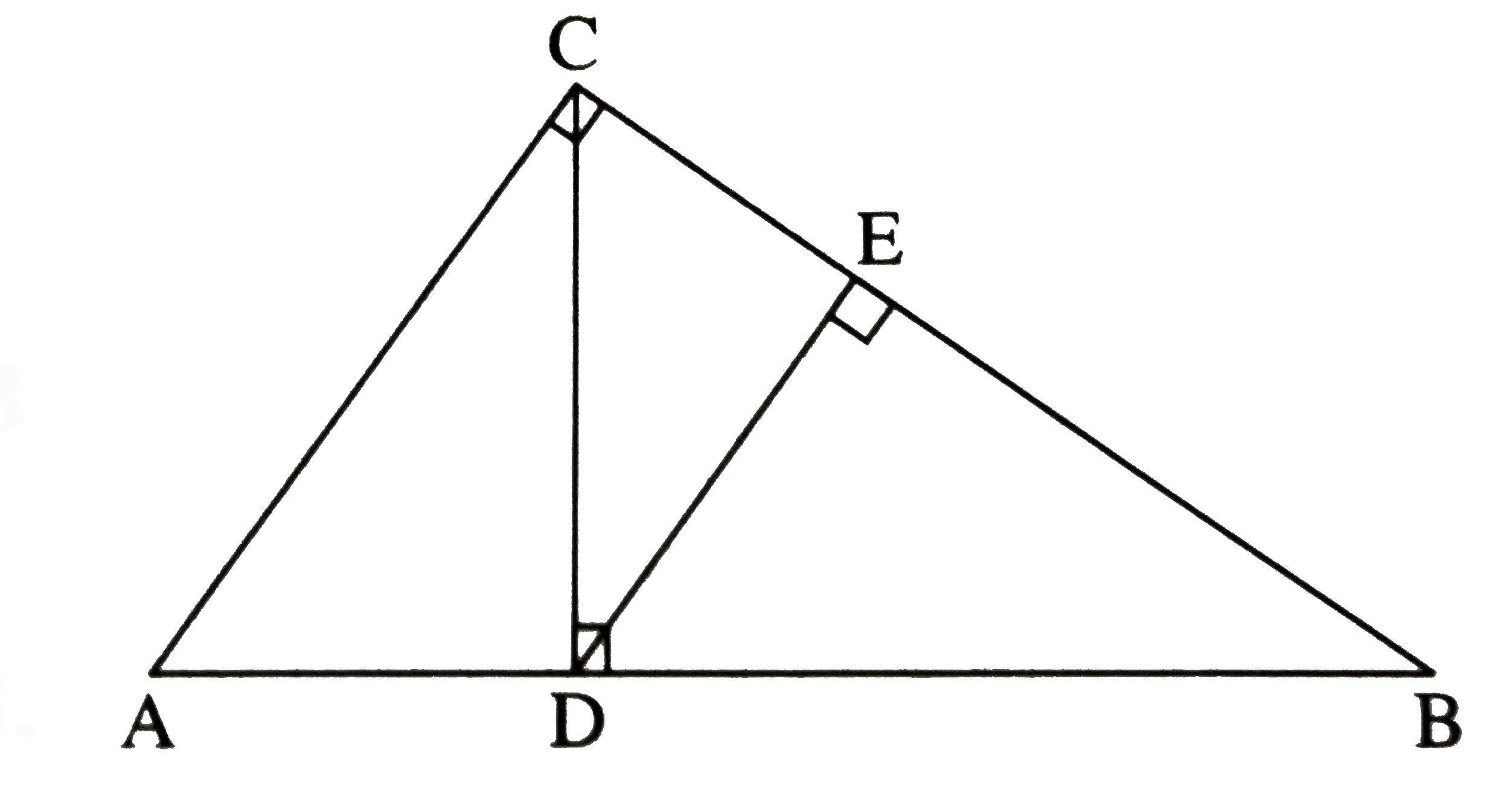
View SolutionIn △ ABC ,
∠ACB=90∘ ,
CD⊥AB and
DE⊥CB
Prove that CD2×AC=AD×AB×DE .
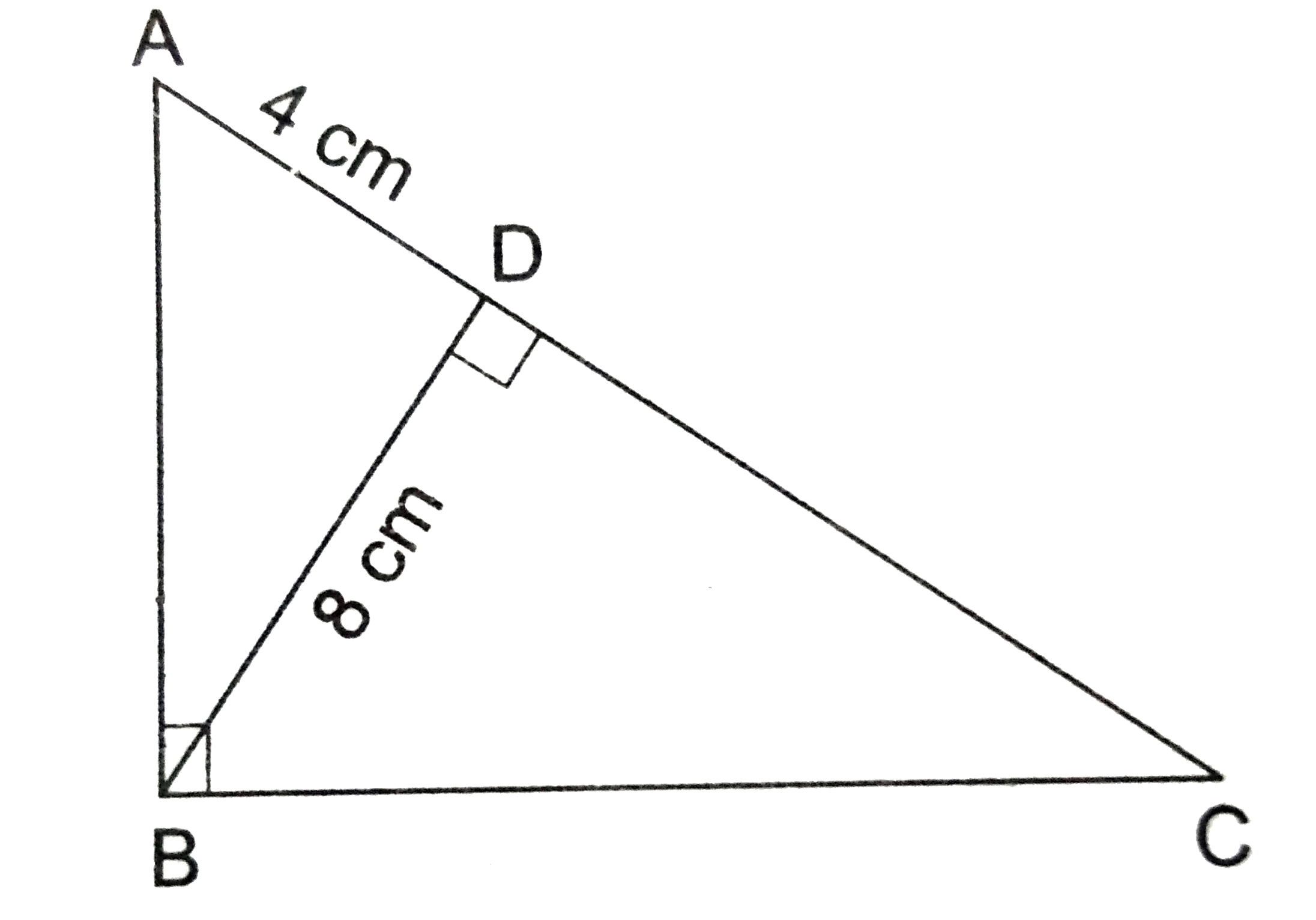
View SolutionIn the given figure, ∠ABC=90∘andBD⊥AC. If BD=8cm,AD=4cm find CD.
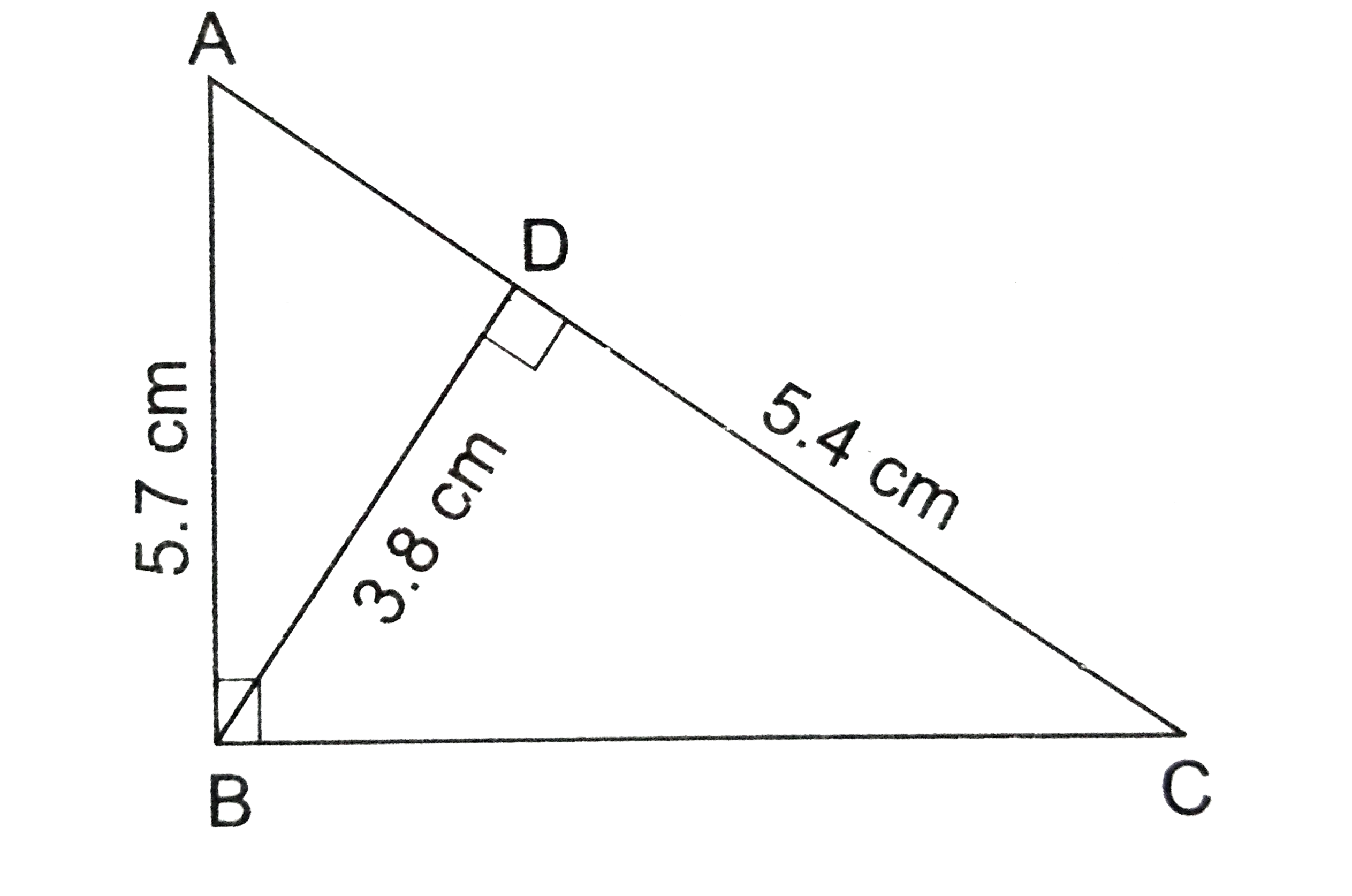
View SolutionIn the given figure, ∠ABC=90∘andBD⊥AC. If AB=5.7cm,BD=3.8cmandCD=5.4cm, find BC.
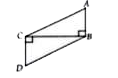
View SolutionIn the given figure, Ab = CD and ∠ABC=∠DCB=90∘. Prove that AC = DB.
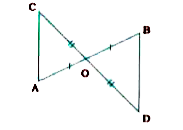
View SolutionIn the given figure AB and CD bisect each other at O. Prove that AC = BD.
View SolutionIn the given figure, AB = CD and AD = CB. Prove that ΔABD≅ΔCDB.

View SolutionIn figure∠ACB=90∘and CD⊥AB. Prove that BC2AC2=BDAD.
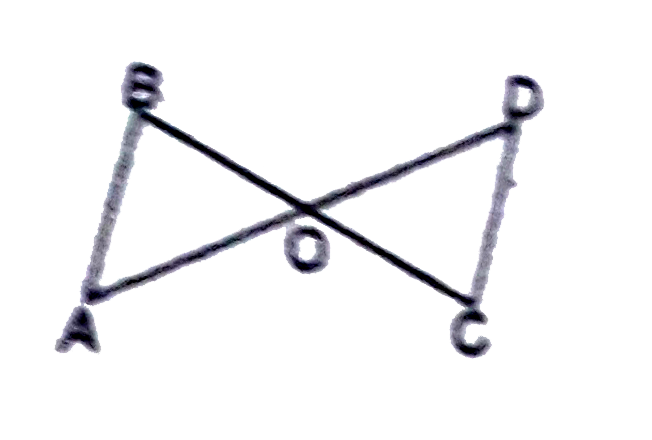
View SolutionIn the given figure △AOB~△DOC, prove that AB||CD.
View Solution