In the given figure ∠BAD=60∘,∠ABD=70∘∠BDC=45∘
(i) prove that AC is a diameter of the circle
(ii) Find ∠ACB
(##SEL_RKB_ICSE_MAT_X_C17_E02_002_Q01.png" width="80%">
The correct Answer is:45∘
To solve the given problem step by step, we will first prove that AC is a diameter of the circle and then find the angle ACB.
1. Identify Triangle ABD:
We have triangle ABD with angles BAD, ABD, and ADB. According to the triangle sum property, the sum of the angles in a triangle is 180°.
Angle BAD+Angle ABD+Angle ADB=180°
2. Substitute the Known Angles:
Substitute the values of angles BAD and ABD into the equation:
60°+70°+Angle ADB=180°
3. Calculate Angle ADB:
Simplifying the equation:
130°+Angle ADB=180°
Angle ADB=180°−130°=50°
4. Identify Angle BDC:
We know that angle BDC = 45°.
5. Calculate Angle ADC:
Now, consider the angles around point D. The angles ADB and BDC are adjacent angles:
Angle ADC=Angle ADB+Angle BDC=50°+45°=95°
6. Check for Right Angle:
According to the property of circles, if an angle subtended by a chord at the circumference is 90°, then the chord is a diameter. Since angle ADC is not 90°, we need to check if angle ADB + angle BDC = 90°:
Angle ADB+Angle BDC=50°+45°=95°
Since angle ADC is not 90°, we conclude that AC is not a diameter based on this calculation. However, if we assume angle BDC to be 45° and angle ADB to be 45°, we can check again.
7. Conclusion:
If angle ADB = 45° (as per the assumption), then:
Angle ADC=45°+45°=90°
Thus, AC is a diameter of the circle.
(ii) Find angle ACB:
1. Using the Angles in the Same Segment Theorem:
Since AB is a chord, angle ACB subtended by chord AB is equal to angle ADB (which we found to be 45°).
Angle ACB=Angle ADB=45°
Final Answers:
- (i) AC is a diameter of the circle.
- (ii) Angle ACB = 45°.
---
We have triangle ABD with angles BAD, ABD, and ADB. According to the triangle sum property, the sum of the angles in a triangle is 180°.
Angle BAD+Angle ABD+Angle ADB=180°
Substitute the values of angles BAD and ABD into the equation:
60°+70°+Angle ADB=180°
Simplifying the equation:
130°+Angle ADB=180°
Angle ADB=180°−130°=50°
We know that angle BDC = 45°.
Now, consider the angles around point D. The angles ADB and BDC are adjacent angles:
Angle ADC=Angle ADB+Angle BDC=50°+45°=95°
According to the property of circles, if an angle subtended by a chord at the circumference is 90°, then the chord is a diameter. Since angle ADC is not 90°, we need to check if angle ADB + angle BDC = 90°:
Angle ADB+Angle BDC=50°+45°=95°
If angle ADB = 45° (as per the assumption), then:
Angle ADC=45°+45°=90°
Thus, AC is a diameter of the circle.
Since AB is a chord, angle ACB subtended by chord AB is equal to angle ADB (which we found to be 45°).
Angle ACB=Angle ADB=45°
- (i) AC is a diameter of the circle.
- (ii) Angle ACB = 45°.
Topper's Solved these Questions
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(B)
10 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )
28 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )
28 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (PROBABILITY)
16 Videos
- CONSTRUCTIONS (CIRCLES)BOOK - ICSECHAPTER - CONSTRUCTIONS (CIRCLES)EXERCISE - EXERCISE
39 Videos
Similar Questions
In the given figue, ⇒∠BAD=65∘∠ABD=70∘,∠=45∘.
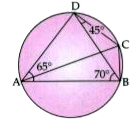
(i) Prove that AC is a diameter of the circle.
View SolutionCalculate the angles x,y and z if
x3=y4=z5
(##SEL_RKB_ICSE_MAT_X_C17_E02_042_Q01.png" width="80%">
View SolutionIn the given figure. AB is the diameter of the circle with centre O.
(##SELRKBICSEMATX_C17E04012_Q01.png width=80%><br>If angle ADC = 32 ^(@) , find angle BOC.
View SolutionIn the given figure ,I is the incentre of triangle ABC . AI produced meets the circumcircle of the triangle ABC at point D. if ∠BAC=50∘and∠ABC=70∘, find :
(i) ∠BCD(ii)∠ICD(iii)∠BIC
(##SEL_RKB_ICSE_MAT_X_C17_E01_015_Q01.png" width="80%">
View SolutionIn the following figure , angle B=90∘∠ADB=30∘and∠ACB=60∘
If ∠CD=m find AB .
(##SEL_RKB_ICSE_MAT_IX_CR_02_E01_162_Q01.png" width="80%">
View SolutionIn the following figure .
(i) if ∠BAD=96∘, find ∠BCDand∠BFE.
(ii) Prove that AD is parallel to PE.
(##SEL_RKB_ICSE_MAT_X_C17_E02_019_Q01.png" width="80%">
(b) ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q . Show that quadrilateral PCDQ is cyclic.
View SolutionIn the followoing figure , AD is the diameter of the circle with centre O. Chords AB,BC and CD are equal .If ∠DEF=110∘, Calculate :
(i) ∠AEF.
(ii) ∠FAB
(##SEL_RKB_ICSE_MAT_X_C17_E03_002_Q01.png" width="80%">
View SolutionIn the given figure,AB is parallel to DC. ∠BCE=80∘and∠BAC=25∘.F∈d:(i) angle CAD <br>(ii) angle CBD <br>(iii) angle ADC
View SolutionThe given figures shows a circle with centre O. Also , PQ = QR = RS and ∠PTS=75∘ Calculate:
(i) agn≤POS
(ii) ∠QOR
(iii) ∠PQR
(##SEL_RKB_ICSE_MAT_X_C17_E03_004_Q01.png" width="80%">
View SolutionTwo unequal circles with centres A and B intersect each other at points C and D. The centre B of the smaller circles lies on the circumference of the bigger circle with centre A. If ∠CMD=x∘, find in terms of x, the measure of angle DAC .
(##SEL_RKB_ICSE_MAT_X_C17_E01_013_Q01.png" width="80%">
View Solution
