In the given figure,AB is parallel to DC. ∠BCE=80∘and∠BAC=25∘.F∈d:(i) angle CAD <br>(ii) angle CBD <br>(iii) angle ADC
The correct Answer is:14cm
To solve the problem step by step, we will use the properties of parallel lines and angles in cyclic quadrilaterals.
Given:
- AB is parallel to DC
- ∠BCE = 80°
- ∠BAC = 25°
To find:
(i) ∠CAD
(ii) ∠CBD
(iii) ∠ADC
Step 1: Find ∠CAD
Since AB is parallel to DC, we can use the property of alternate interior angles. The exterior angle ∠BCE is equal to the interior opposite angle ∠BAD.
Thus, we have:
∠BAD=∠BCE=80°
Now, we can find ∠CAD using the relationship:
∠CAD=∠BAD−∠BAC
Substituting the known values:
∠CAD=80°−25°=55°
Step 2: Find ∠CBD
Since angles CAD and CBD subtend the same arc AC in the cyclic quadrilateral ABCD, they are equal:
∠CBD=∠CAD=55°
Step 3: Find ∠ADC
In the isosceles trapezium ABCD, the angles ∠ADC and ∠BCD are equal because they are angles on the same segment. We can find ∠ADC using the fact that the sum of angles in a triangle is 180°.
We know:
∠BCD=∠BCE=80°
Thus,
∠ADC+∠BCD=180°
Substituting the known value:
∠ADC+80°=180°
Solving for ∠ADC:
∠ADC=180°−80°=100°
Final Answers:
(i) ∠CAD = 55°
(ii) ∠CBD = 55°
(iii) ∠ADC = 100°
- AB is parallel to DC
- ∠BCE = 80°
- ∠BAC = 25°
(i) ∠CAD
(ii) ∠CBD
(iii) ∠ADC
∠BAD=∠BCE=80°
∠CAD=∠BAD−∠BAC
Substituting the known values:
∠CAD=80°−25°=55°
∠CBD=∠CAD=55°
∠BCD=∠BCE=80°
Thus,
∠ADC+∠BCD=180°
Substituting the known value:
∠ADC+80°=180°
Solving for ∠ADC:
∠ADC=180°−80°=100°
(i) ∠CAD = 55°
(ii) ∠CBD = 55°
(iii) ∠ADC = 100°
Topper's Solved these Questions
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(B)
10 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (PROBABILITY)
16 Videos
- CONSTRUCTIONS (CIRCLES)BOOK - ICSECHAPTER - CONSTRUCTIONS (CIRCLES)EXERCISE - EXERCISE
39 Videos
Similar Questions
In the given figure, find ∠ABC.

View SolutionIn the given figure, find ∠AOB.

View SolutionIn the given arc AB= twice are BC and ∠AOB=80∘ find:
∠OAC
View SolutionIn the given arc AB= twice are BC and ∠AOB=80∘ find:
∠BOC
View SolutionIn the given below AB is parallel to CD and CA = CE .
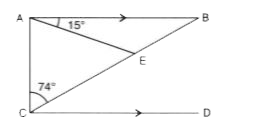
If angle ACE = 74∘and∠EAB=15∘ find the angles AEB and BCD.
View SolutionIn the given figure ,I is the incentre of triangle ABC . AI produced meets the circumcircle of the triangle ABC at point D. if ∠BAC=50∘and∠ABC=70∘, find :
(i) ∠BCD(ii)∠ICD(iii)∠BIC
(##SEL_RKB_ICSE_MAT_X_C17_E01_015_Q01.png" width="80%">
View SolutionIn the given figure, find ∠ADB, if ∠DCB=100∘ and ∠DBA=70∘.

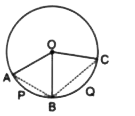
View SolutionIn the given figure , arc APB : arc BQC = 2: 3 and ∠AOC=150∘, Find :
(i) ∠AOB
(ii) ∠BOC
(iii) ∠OBA
(iv) ∠OCB
(v) ∠ABC
View SolutionIn the given figure, ABCD is a trapezium with angle C=120∘,DC=28 cm and BC=40 cm. Find :
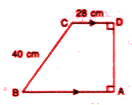
(i) AB
View SolutionIn the given figure, find ∠D and ∠B.

View Solution