In the given figure, , seg PQ seg RQ. Prove that .
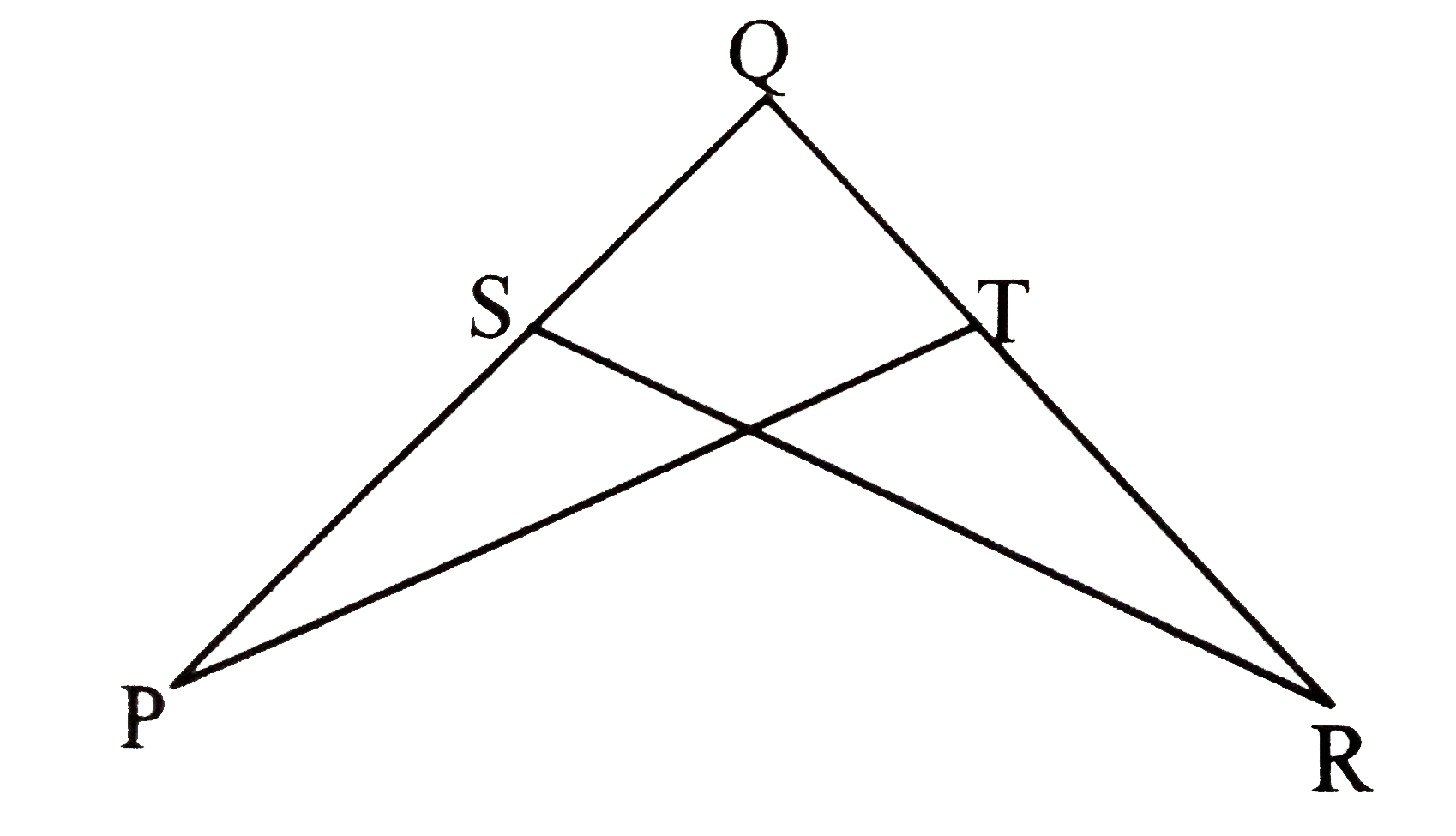
Step by step video & image solution for In the given figure, angleP~=angleR , seg PQ ~= seg RQ. Prove that DeltaPQT~=DeltaRQS . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHALLENGING QUESTIONS BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - QUADRILATERALS
16 Videos
- CHALLENGING QUESTIONS BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - SURFACE AREA AND VOLUME
25 Videos
- CHALLENGING QUESTIONS BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - PARALLES LINES
11 Videos
- BOARD QUESTION PAPER: MARCH 2019BOOK - TARGET PUBLICATIONCHAPTER - BOARD QUESTION PAPER: MARCH 2019EXERCISE - (Solve the following questions (Any one):
4 Videos
- CIRCLEBOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Chapter Assessment
9 Videos
Similar Questions
In the given figure, ∠PQR=90∘, seg QN⊥segPR,PN=9,NR=16.Find QN.
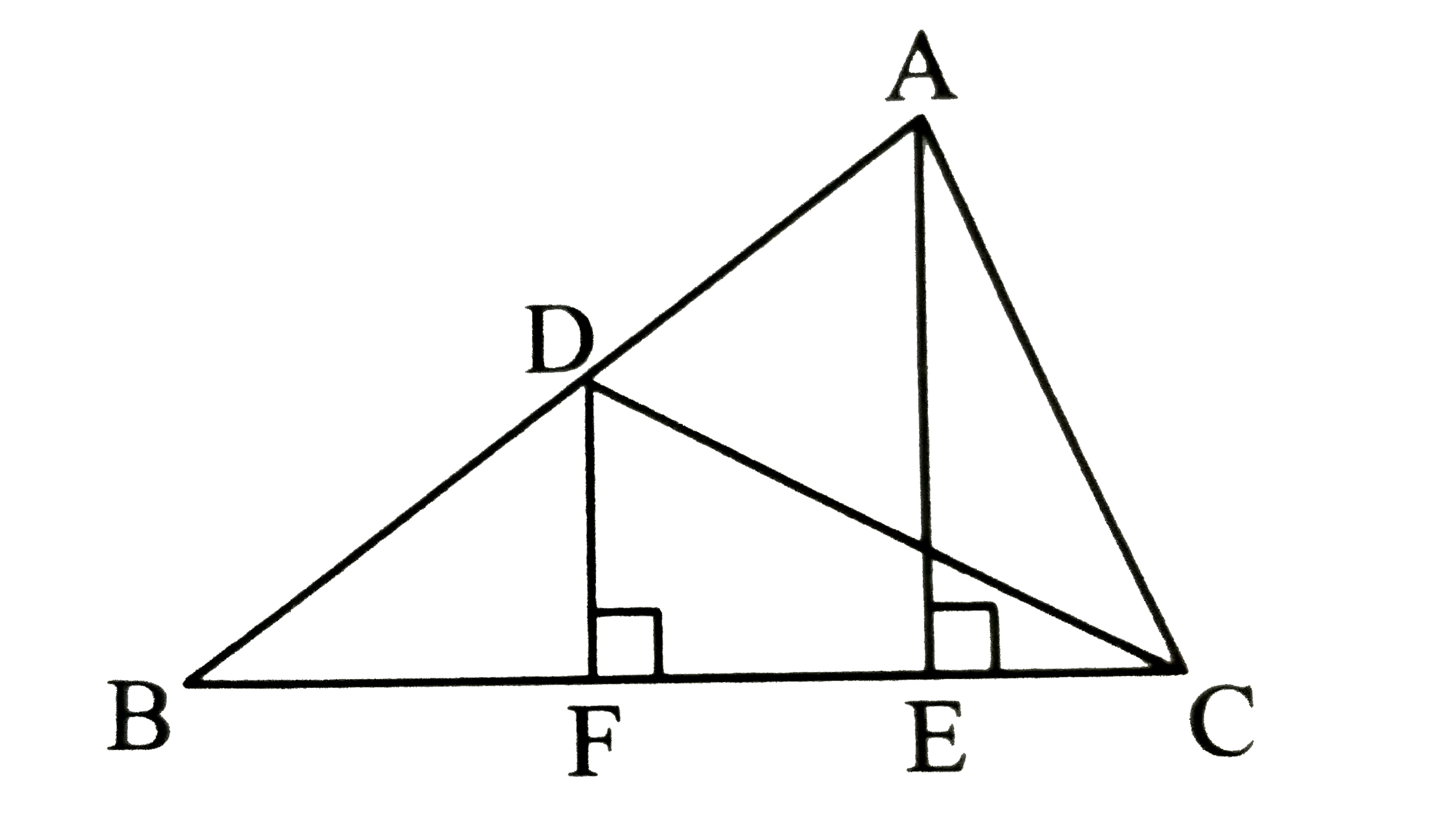
View SolutionIn the given figure, seg AE⊥ seg BC and seg DF ⊥seg BC. Find
i.A(ΔABC)A(ΔDBC)
ii. A(ΔDBF)A(ΔDFC)
iii. A(ΔAEC)A(ΔDBF)
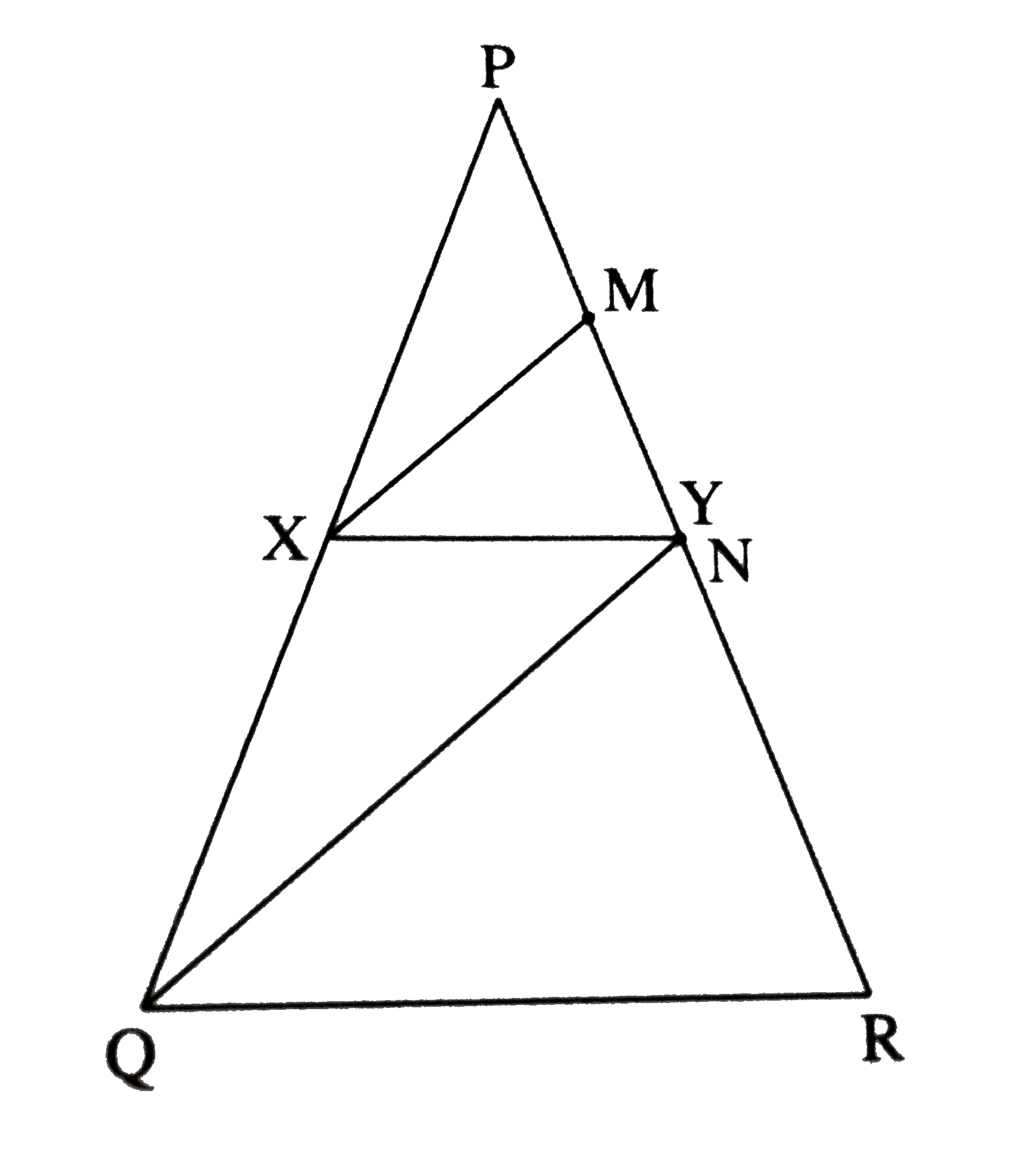
View SolutionIn ΔPQR, set XY∣∣ sides QR, M and N are midpoints of seg PY and seg PR respectively. Prove that:
(i) ΔPXM~ΔPQN (ii) segXM∣∣secQN.
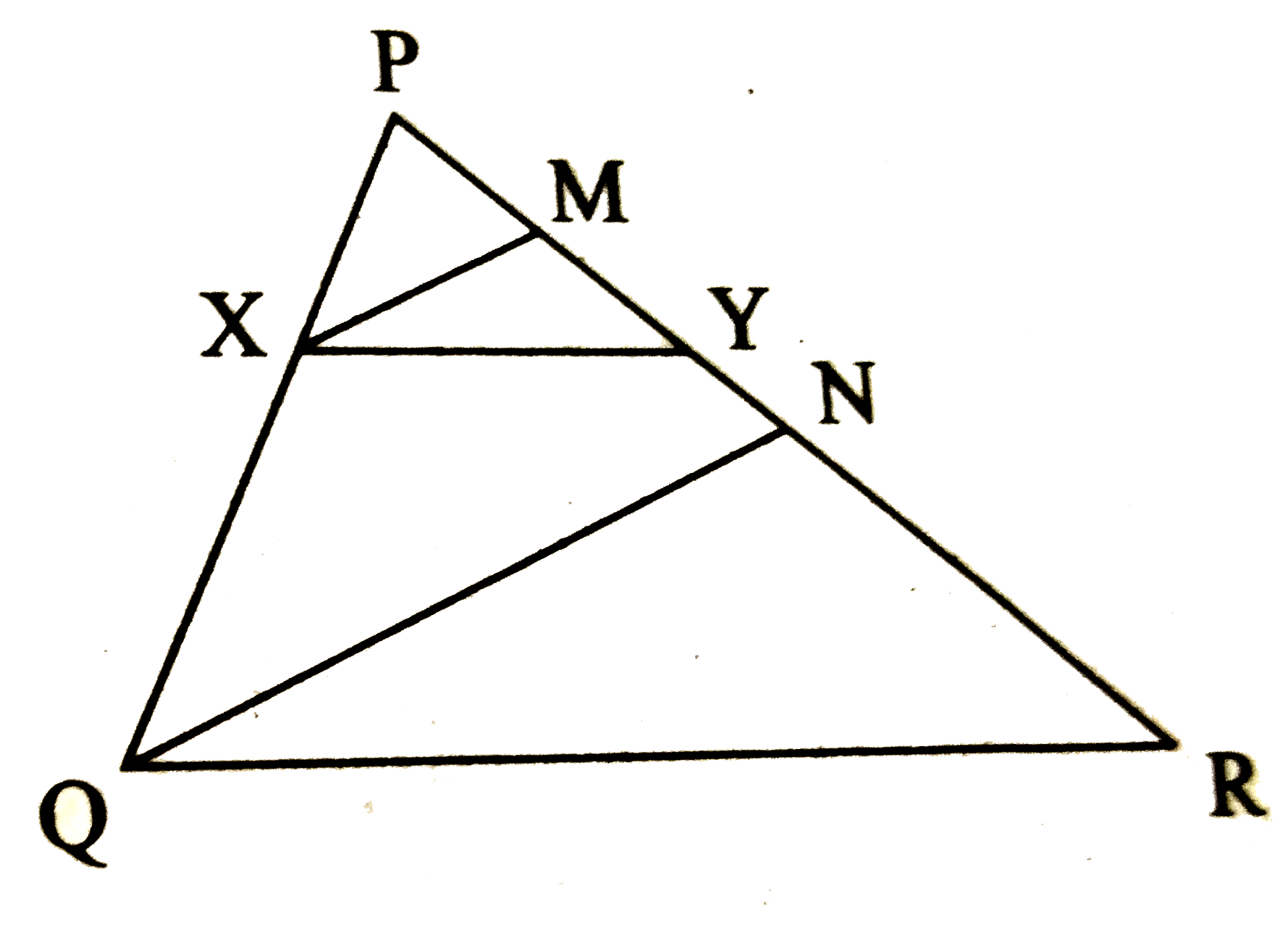
View SolutionIn ΔPQR, seg XY∣∣ side QR. M and N are the midpoints of seg PY and side PR respectively, P−M−Y−N−R.
Prove that (i)ΔPXM~ΔPQN
(ii) seg XM∣∣ seg QN.
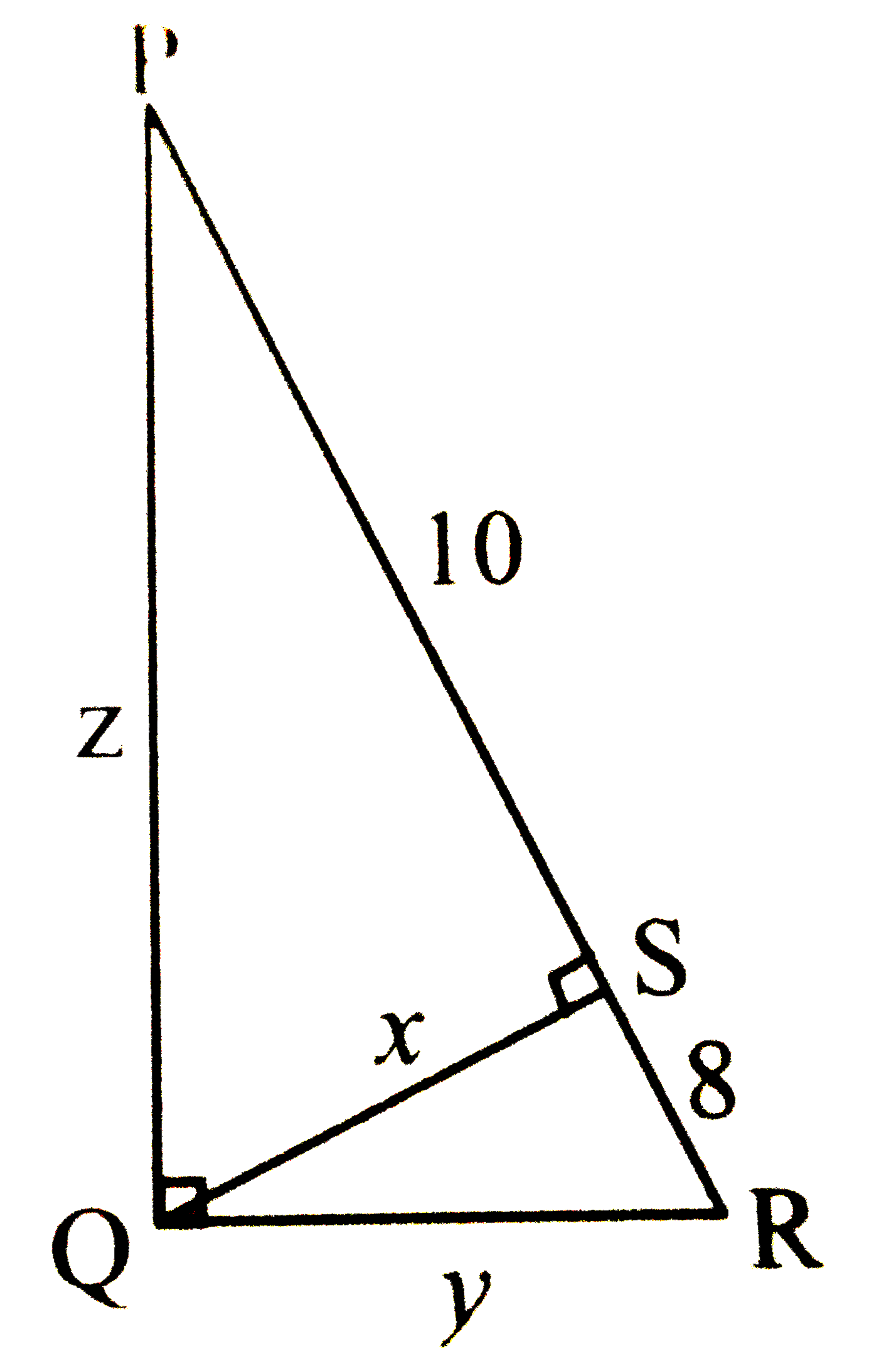
View SolutionSee the given figre. In ΔPQR,∠PQR=90∘, seg QS⊥ seg PR, then find x,y,z.
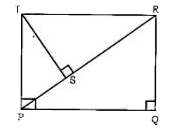
View SolutionIn the figure, RQ⊥PQ, PQ⊥PT and ST⊥PR. Prove that: ST × QR = PS × PQ
View SolutionIn the adjoining figure, seg PA , seg QB, seg RC and seg SD are perpendicular to line AD. AB = 60, BC = 70, CD = 80, PS = 280, then find PQ, QR and RS.

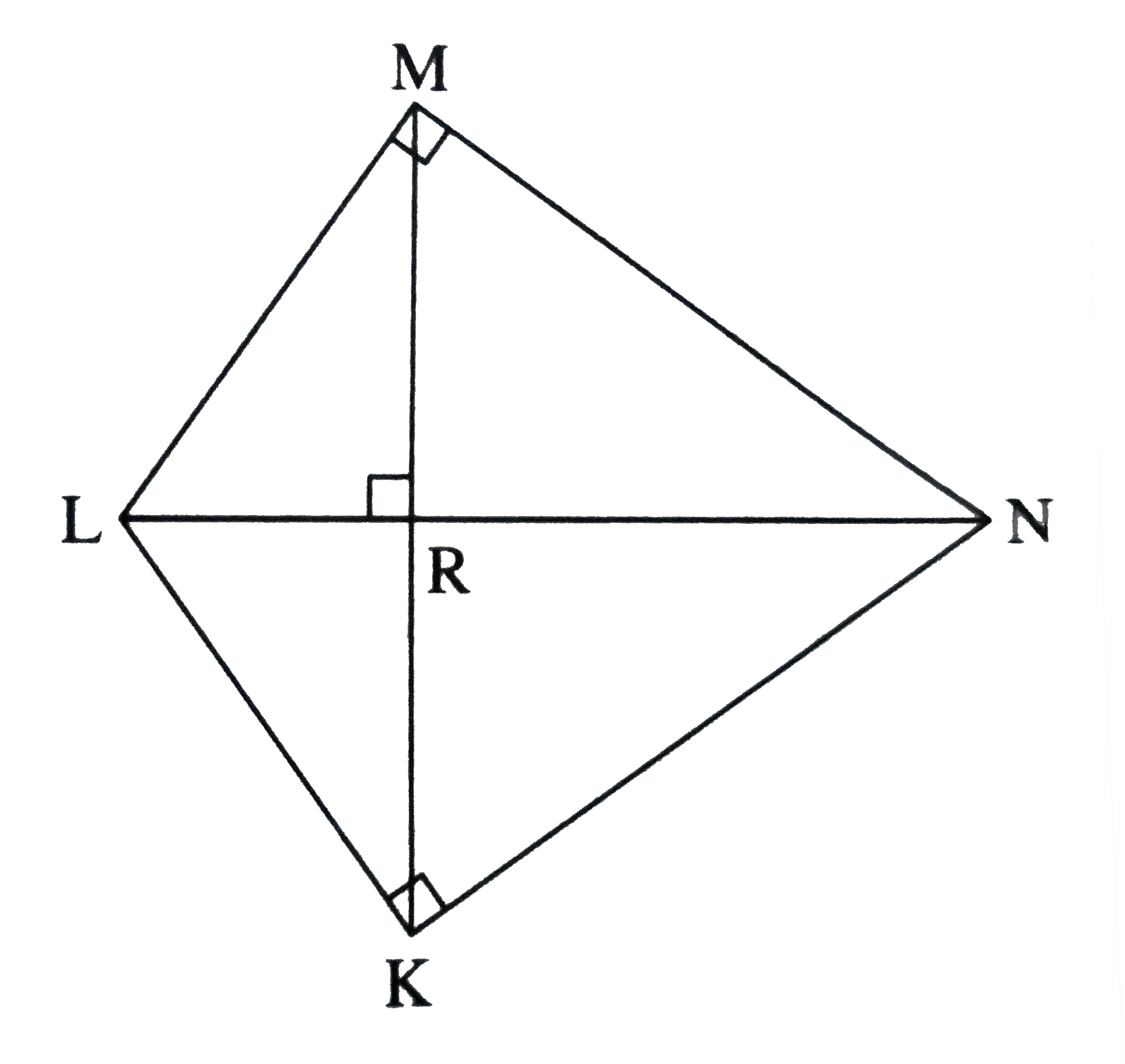
View SolutionIn the figure , ∠LMN=∠LKN=90∘
seg MK ⊥ seg LN .
Complete the following activtiy
to prove R is the midpoint of seg MK .
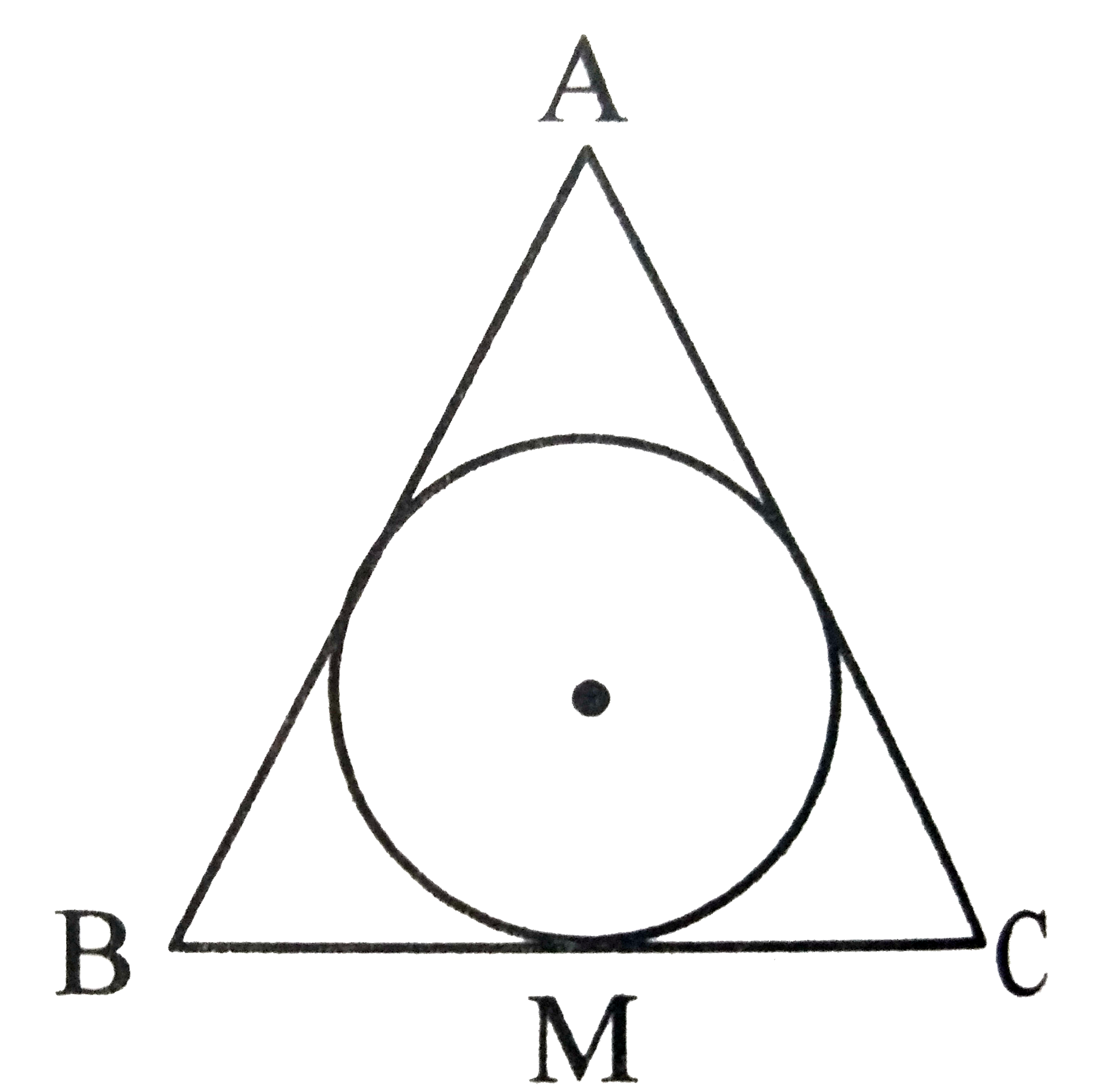
View SolutionIn the adjoining figure, the circle is the incircle of isosceles ΔABC, where seg AB=seg AC. Prove that M bisects BC.
View SolutionSee the given figure. In ΔABC, seg AD⊥ seg BC. Prove that: AB2+CD2=BD2+AC2
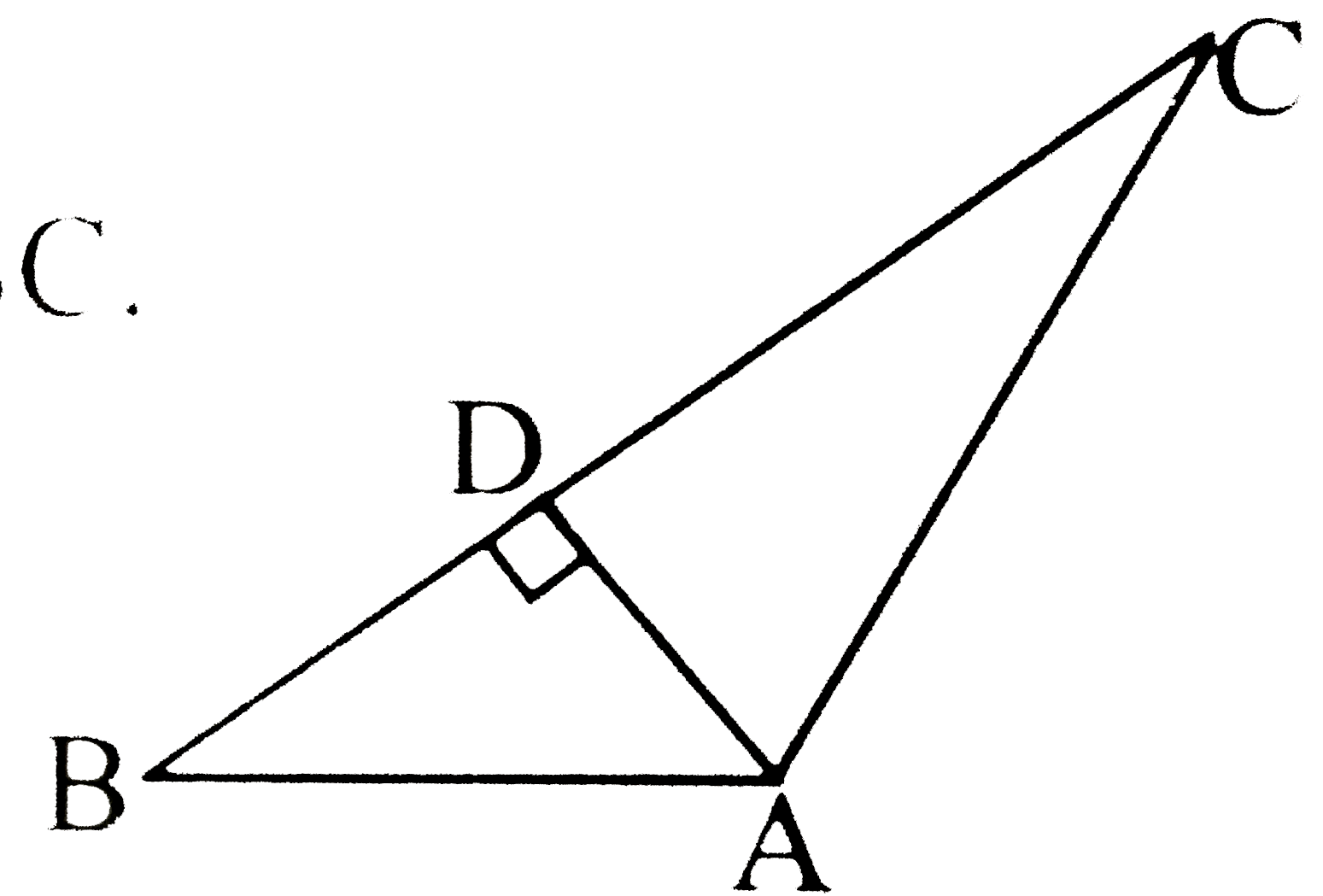
View Solution
