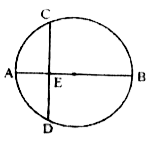
In the given figure, CD is the diameter of a circle with centre O and CD is perpendicular to chord AB. If AB = 12 cm and CE=3cm then radius of the circle is
The correct Answer is:7.5 cm
Let OA = OC = r cm . Then, OE =(r−3) cm and AE =12AB=6 cm.
Use OA2=OE2+AE2.
Similar Questions
Knowledge Check
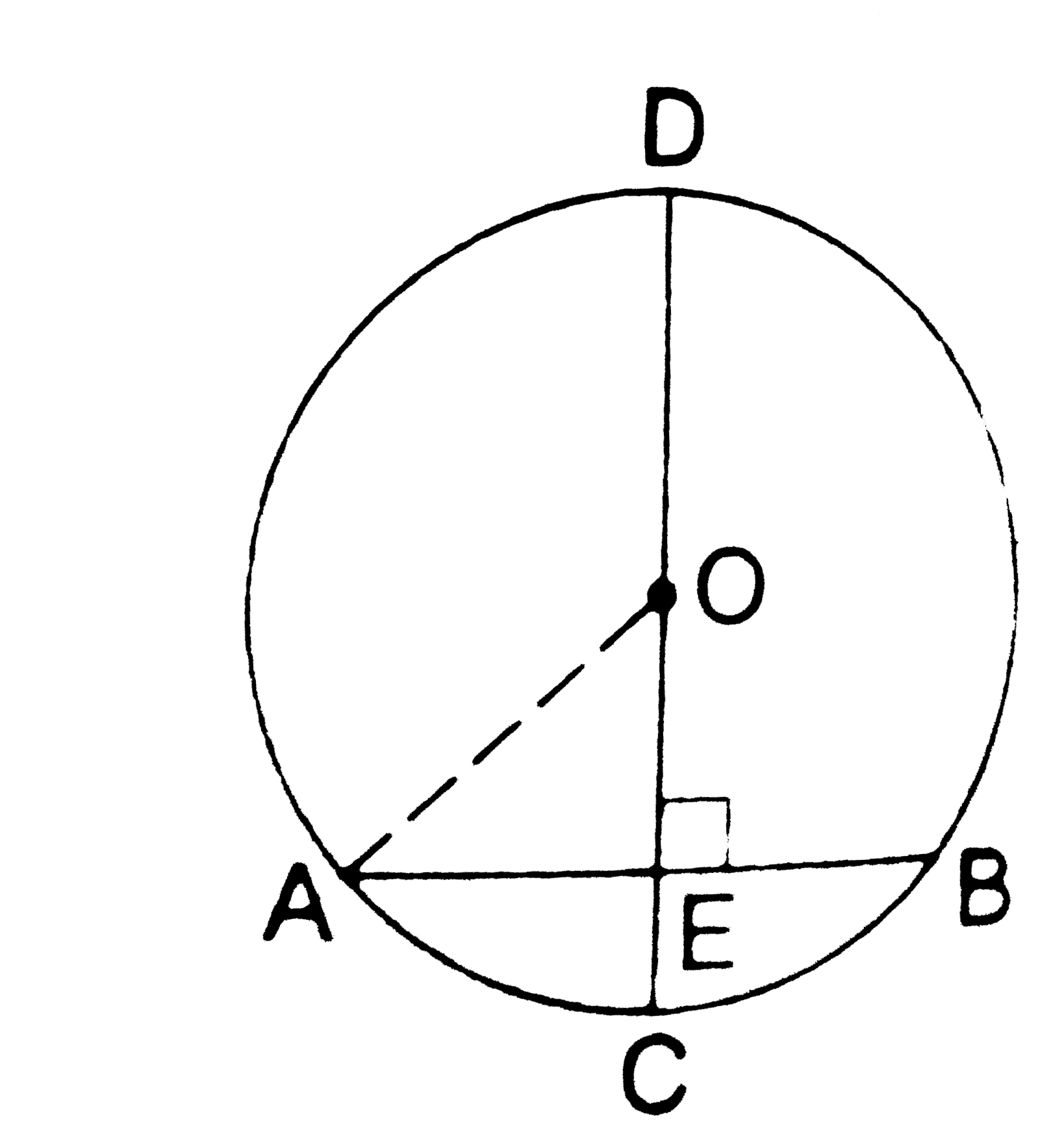
In the given figure, O is the centre of a circle of radius 13 cm and AB is a chord perpendicular to OD. If CD = 8 cm, then what is the length (in cm) of AB?
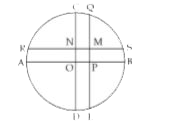
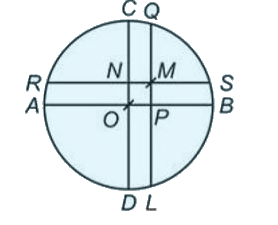
AA)6 cmBB)12 cmCC)24 cmDD)28cmIn the given figure, CD and AB are diameters of circle and AB and CD are perpendicular to each other. LQ and SR are perpendiculars to AB and CD respectively. Radius of circle is 5 cm, PB: PA = 2:3 and CN:ND = 2:3. What is the length (in cm) of SM?
A[(5√3)−3]B[(4√3)−2]C[(2√5)−1]D[(2√6)−1]In the given figure, O is the centre of the circle. AB is tangent. AB=12cmandOB=13cm. Find OA:
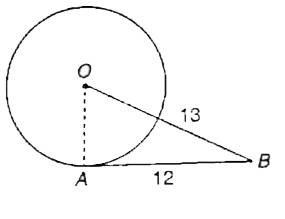A6.5 cmB6 cmC5 cmDnone of these
In the given figure, AB and CD are two diameters of a circle (with centre 0) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
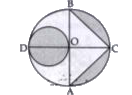
View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
View SolutionIn the given figure, CD and AB are diameters of circle and AB and CD are perpendicular to each other. LQ and SR are perpendiculars to AB and CD respectively. Radius of circle is 5 cm, PB: PA = 2:3 and CN:ND = 2:3. What is the length (in cm) of SM?
View SolutionIn the given figure, CD and AB are diameters of circle and AB and CD are perpendicular to each other .LQ and SR are perpendiculars to AB and CD respectively . Radius of circle is 5 cm , PB : PA = 2 : 3 and CN : ND = 2 : 3 . What is the length (in cm) of SM ?
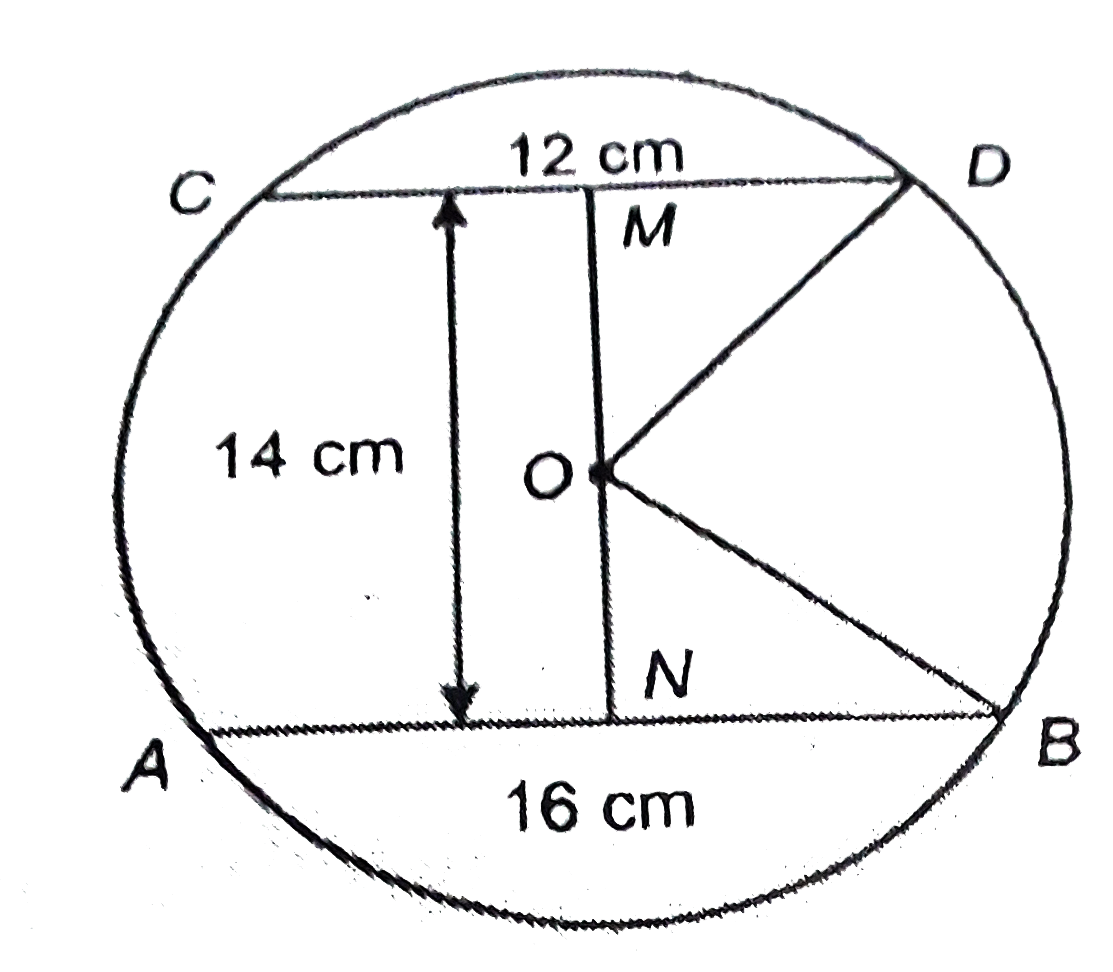
View SolutionIn the adjoining figure ,AB and CD are two parallel chords of a circle with centre O , whose length are 16 cm and 12 cm respectively. Find the radius of the circle if the distance between them is 14 cm.
View Solution