In the given figure, CD || LA and DE || AC. Find the length of CL if BE = 4 cm and EC = 2 cm
The correct Answer is:3 cm
To solve the problem step by step, we will use the properties of similar triangles and Thales' theorem.
1. Identify the Triangles and Parallel Lines:
- We have two sets of parallel lines: CD || LA and DE || AC. This indicates that we can use Thales' theorem in both triangles ABL and ABC.
2. Apply Thales' Theorem in Triangle ABL:
- According to Thales' theorem, if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
- For triangle ABL, we can write the proportion:
BDDA=BCCL(Equation 1)
3. Apply Thales' Theorem in Triangle ABC:
- Similarly, for triangle ABC, we can apply Thales' theorem:
BDDA=BEEC(Equation 2)
4. Set the Two Equations Equal:
- Since both equations equal BDDA, we can set them equal to each other:
BCCL=BEEC
5. Substitute Known Values:
- We know that BE=4cm and EC=2cm. Therefore, we can substitute these values into the equation:
BCCL=42
- Simplifying gives:
BCCL=2
6. Express BC in Terms of CL:
- From the previous step, we can express BC as:
BC=2⋅CL
7. Substitute BC Back into the Equation:
- Now we can substitute BC back into the equation we derived from Thales' theorem:
BE+ECCL=42
- Since BC=BE+EC, we have:
4+2CL=2
8. Solve for CL:
- This simplifies to:
6CL=2
- Cross-multiplying gives:
6=2⋅CL
- Dividing both sides by 2 results in:
CL=3cm
Final Answer:
The length of CL is 3 cm.
- We have two sets of parallel lines: CD || LA and DE || AC. This indicates that we can use Thales' theorem in both triangles ABL and ABC.
- According to Thales' theorem, if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
- For triangle ABL, we can write the proportion:
BDDA=BCCL(Equation 1)
- Similarly, for triangle ABC, we can apply Thales' theorem:
BDDA=BEEC(Equation 2)
- Since both equations equal BDDA, we can set them equal to each other:
BCCL=BEEC
- We know that BE=4cm and EC=2cm. Therefore, we can substitute these values into the equation:
BCCL=42
- Simplifying gives:
BCCL=2
- From the previous step, we can express BC as:
BC=2⋅CL
- Now we can substitute BC back into the equation we derived from Thales' theorem:
BE+ECCL=42
- Since BC=BE+EC, we have:
4+2CL=2
- This simplifies to:
6CL=2
- Cross-multiplying gives:
6=2⋅CL
- Dividing both sides by 2 results in:
CL=3cm
The length of CL is 3 cm.
Topper's Solved these Questions
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (D)
8 Videos
- MATRICESBOOK - ICSECHAPTER - MATRICESEXERCISE - Exercise 9D
25 Videos
- MIXED PRACTICE BOOK - ICSECHAPTER - MIXED PRACTICE EXERCISE - SET B
52 Videos
Similar Questions
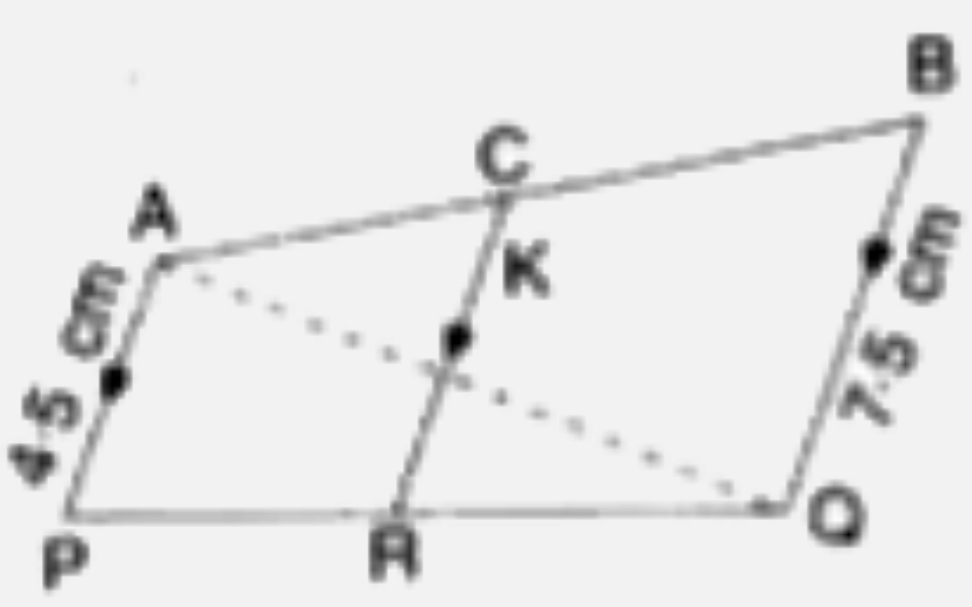
In the given figure, if AC=3cm and CB=6cm, find the length of CR.
View SolutionIn the given figure, DE // BC and AE : EC = 5 : 4. Find :
DE : BC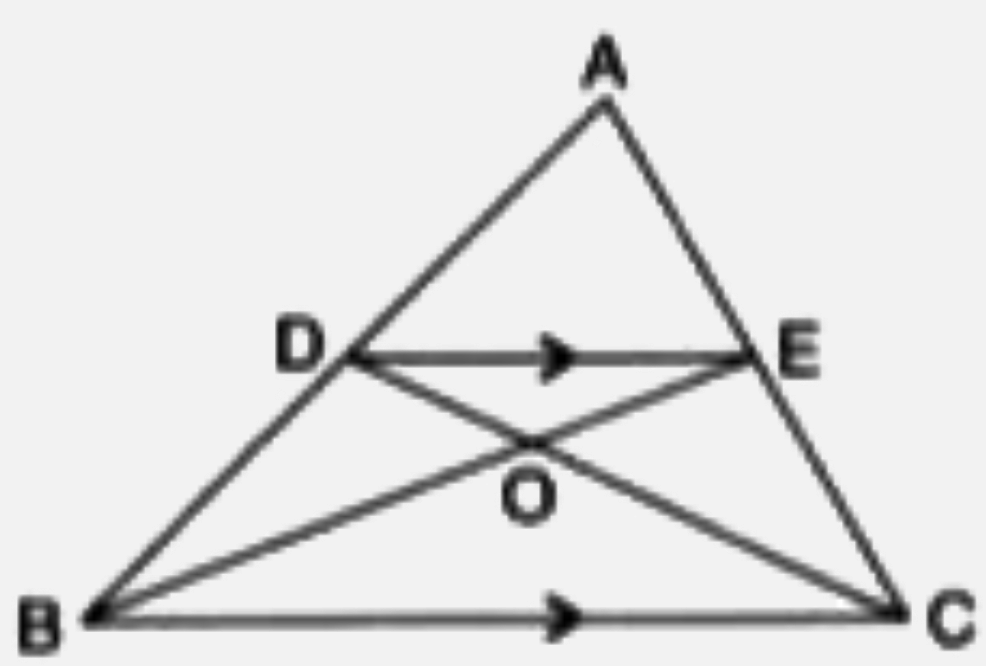
View SolutionIn the given figure, DE // BC and AE : EC = 5 : 4. Find :
DO : DC

View SolutionIn the given figure, AB and DE are perpendiculars to BC
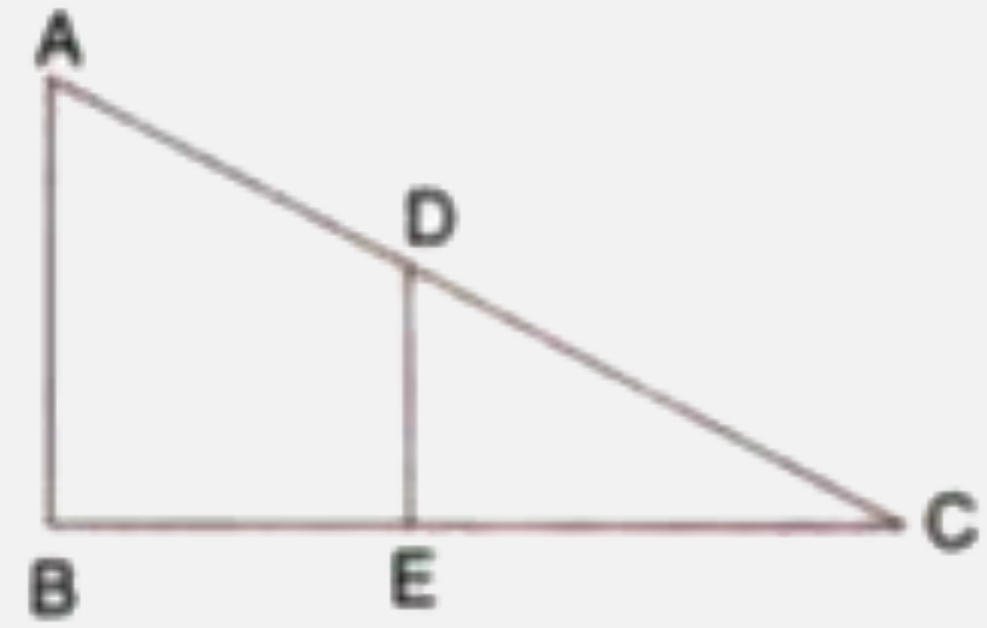
If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
View SolutionIn the given figure, AB and DE are perpendicular to BC. If AB = 6cm, DE = 4cm and AC = 15cm.

(iii) Find the ratio of the area of ΔABC : area of ΔDEC.
View SolutionIn the given figure, AB and DE are perpendiculars to BC. If AB = 9 cm, DE = 3 cm and AC = 24 cm, calculate AD.

View SolutionIn the given figure, AB and DE are perpendicular to BC.

(iI) If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
View SolutionIn the given figure, AB∣∣CD,AB=7cm,BD=25cmandCD=17cm, find the length of side BC.

View SolutionIn the given figure DE||AC and DC||AP. Prove that BEEC=BCCP

View SolutionIn the given figure, if AB=AC, rove that BE=EC.
View Solution
