In the given figure, D and E are the points on the base BC of ΔABC such that BD=CE,AD=AE and ∠ADE=∠AED, prove that ΔADB≅ΔAEC.
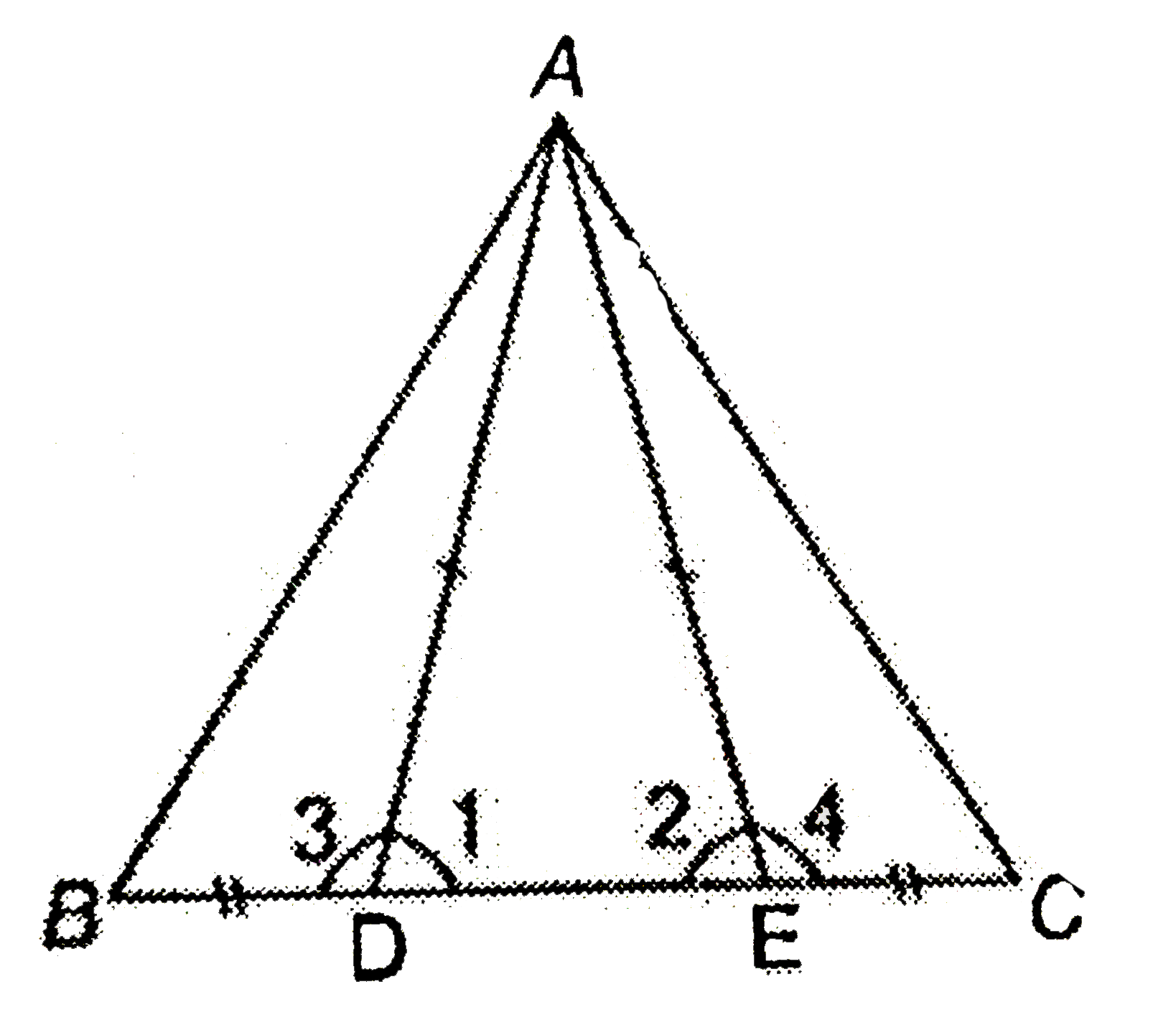
Since ∠1=∠2 (given)
⇒ 180−∠3=180−∠4 (L.P.A.)
⇒ ∠3=∠4
Now, in ΔADB and ΔAEC,
∵⎧⎪⎨⎪⎩BD=CE(given)∠3=∠4(proved above)AD=AE(given)
∴ΔADB≅ΔAEC (SAS) Hence Proved.
Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 7a
35 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
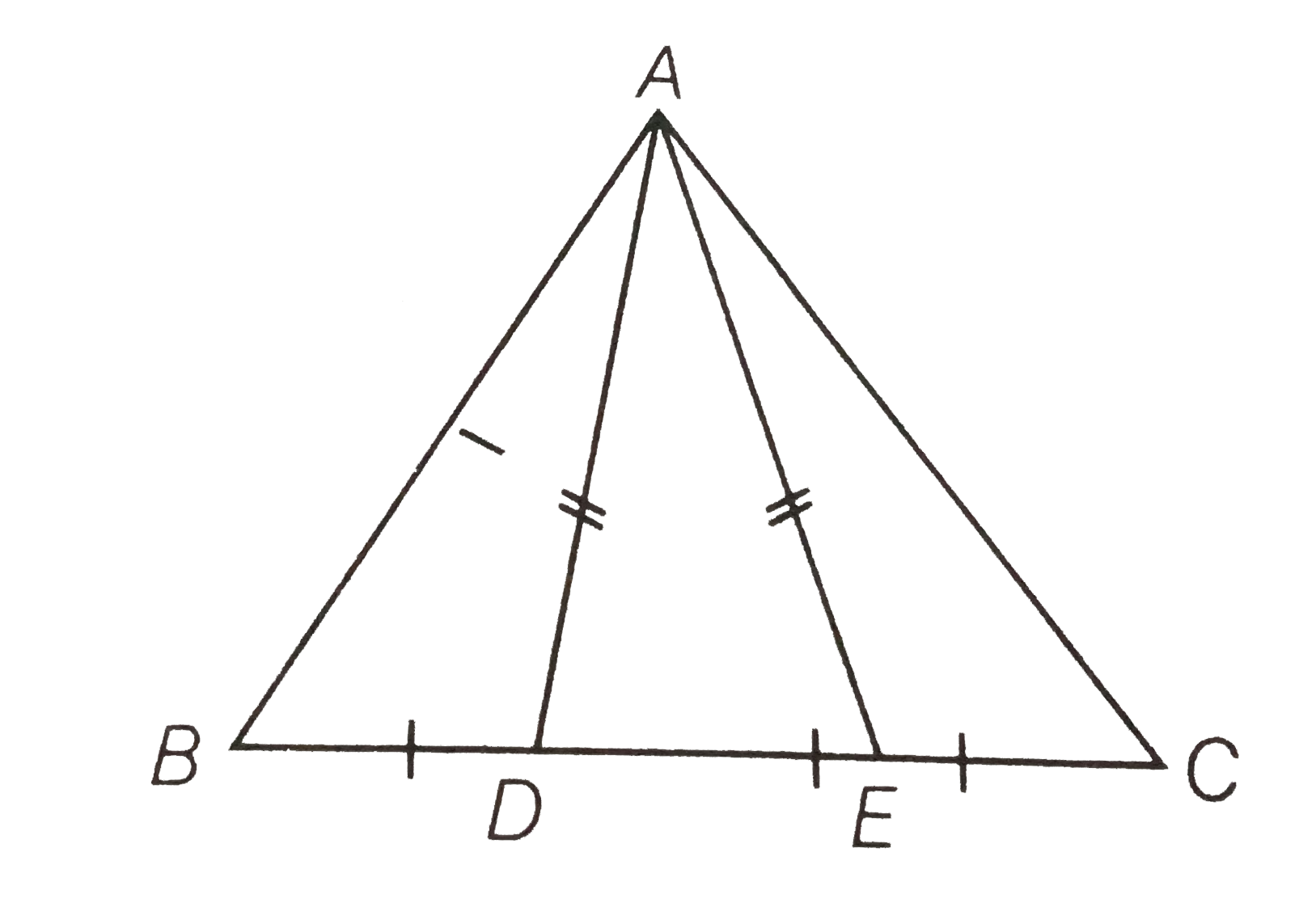
In figure ,D and E are Points on side BC of a ΔABC such that BD=CE and AD=AE. Show that ΔABD≅ΔACE.
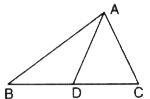
View SolutionIn the given figures, AB > AC and D is any point on BC.
Prove that : AB >AD.
View SolutionIn the given figure, AB and DE are perpendicular to BC.
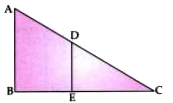
(i) Prove that ΔABC~ΔDEC
View Solutionif D and E are points on the sides AB and AC of a ΔABC. Such that AB=12 cm, AD=8 cm, AE=12 cm, AC= 18 cm. show that DE||BC.
View SolutionIn the given figure, DE // BC.

Prove that ΔADEandΔABC are similar
View SolutionIn the adjoining figure, AD=DC and DB bisects ∠ADC. Prove that ΔADB≅ΔCDB.

View SolutionIn the given figure, AD and CE are medians and DF∣∣CE. Prove that : FB=14AB.
View SolutionIn the given figure, AD and CE are medians and DF||CE. Prove that : Fb=14AB.
View SolutionIn the given figure, AD is altitude and AE is bisector of angle BAC of ΔABC. Show that ΔDAE=12(∠B−∠C)

View SolutionIn the given figure, AC=AE,AB=AD and ∠BAD=∠EAC. Prove that BC=DE.
View Solution
