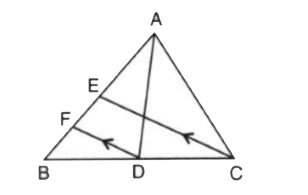
In the given figure, AD and CE are medians and DF∣∣CE. Prove that : FB=14AB.
The correct Answer is:FB=14AB
Step by step video & image solution for In the given figure, AD and CE are medians and DF||CE. Prove that : FB=(1)/(4)AB. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MID-POINT THEOREMEXERCISE - 4 MARKS QUESTION15videos
MID-POINT THEOREM
- BOOK - ICSECHAPTER - MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)EXERCISE - EXERCISE 12(B)23videos
MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)
- BOOK - ICSECHAPTER - PYTHAGORAS THEORAMEXERCISE - QUESTIONS9videos
PYTHAGORAS THEORAM
Similar Questions
In the given figure, AD and CE are medians and DF||CE. Prove that : Fb=14AB.
 View Solution
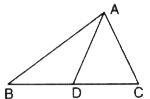
View SolutionIn the given figures, AB > AC and D is any point on BC.
Prove that : AB >AD.
 View Solution
View SolutionIn the given figure, DE||ACandDF||AE.
Prove that BFFE=BEEC
 View Solution
View SolutionIn the given figure, DE||ACandDF||AE.
Prove that BFFE=BEEC
 View Solution
View SolutionIn the given figure D is mid-point of AB. DE//BC and DF //AC . Prove that : DE = BF
 View Solution
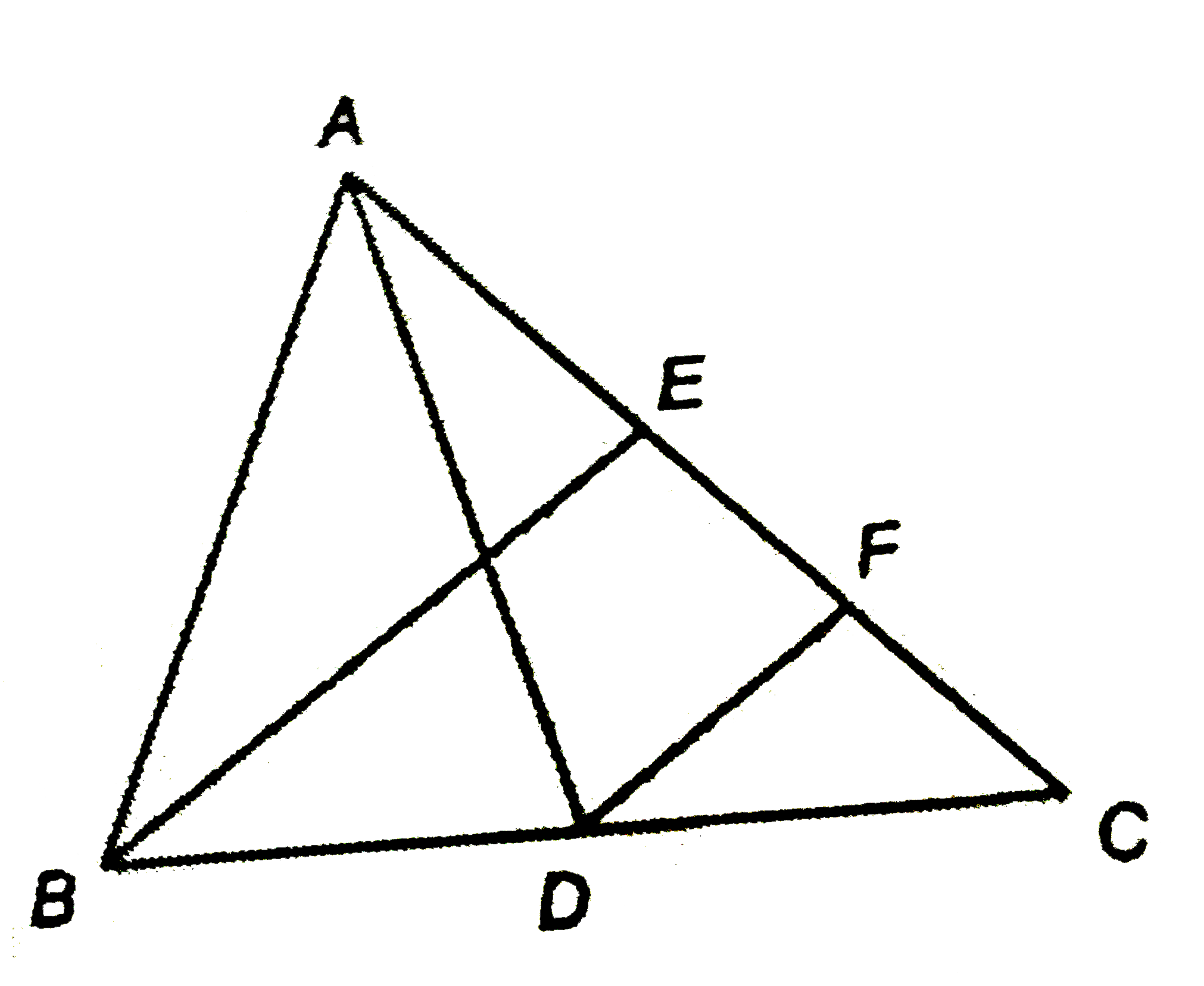
View SolutionIn the adjoining figure. AD and BE are two medians of ΔABC. IfDF||BE,then prove thatCF=14AC.
 View Solution
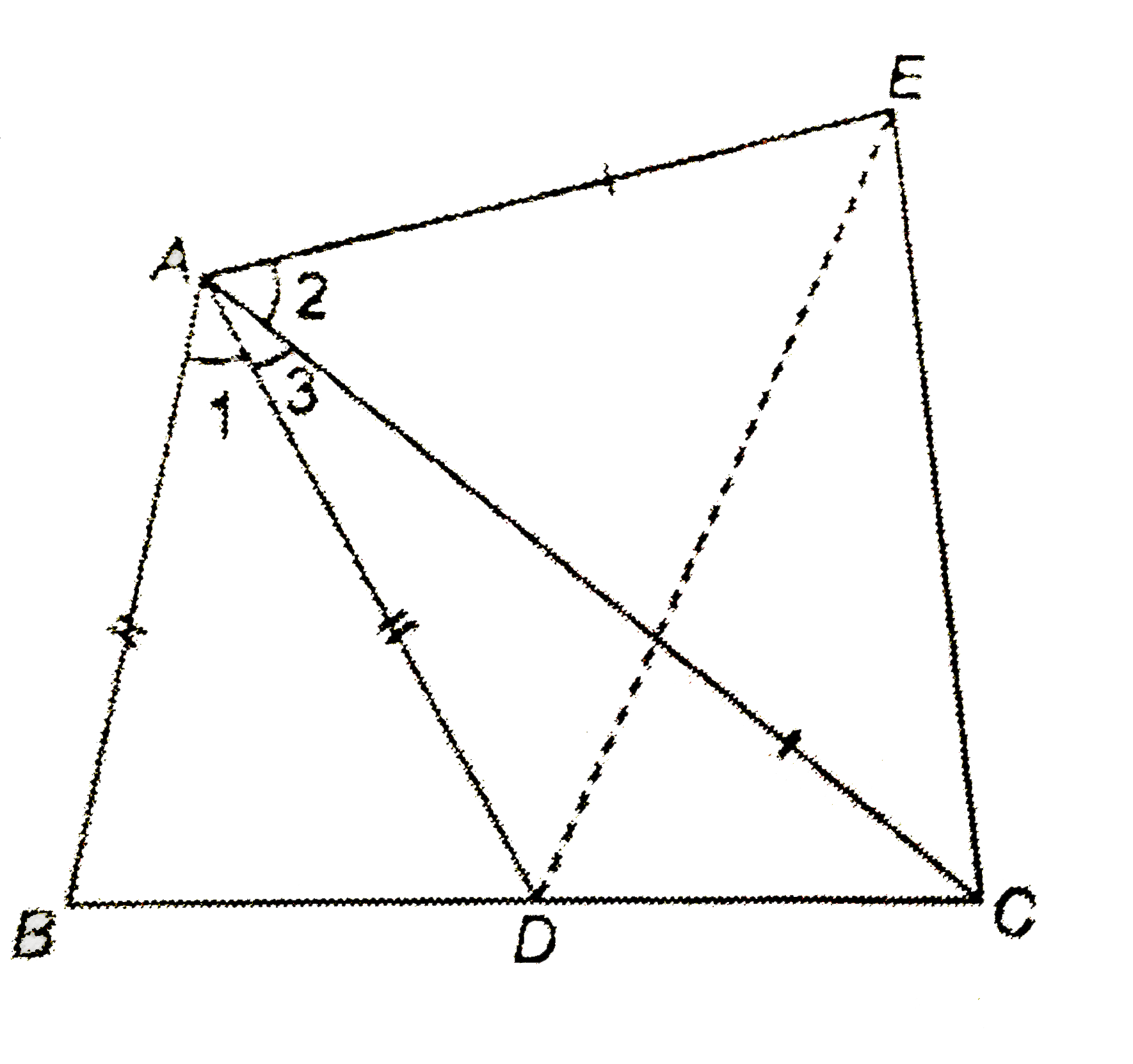
View SolutionIn the given figure, AC=AE,AB=AD and ∠BAD=∠EAC. Prove that BC=DE.
 View Solution
View SolutionIn the given figure, if DE||AQ and DF||AR. Prove that EF||QR.
 View Solution
View SolutionIn the given figure AD and CE are two altitude of △ABC. Prove that. △AEF~△CDF
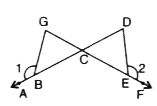
View SolutionIn the given figure , BC = CE and ∠1=∠2.
Prove that :
ΔGCB=ΔDCB .
 View Solution
View Solution

