In the given figure (not drawn to scale), L, M and N are the mid-points of the sides QR, RP and PQ respectively of a ΔPQR. OM intersects the line LN at U and RN intersects the line LM at V, then UV = kQR. Find the value of k.
4
14
2
12
The correct Answer is:B
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018 SET B EXERCISE - Everyday mathematics10videos
IMO QUESTION PAPER 2018 SET B
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018 SET B EXERCISE - Achievers Section5videos
IMO QUESTION PAPER 2018 SET B
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018 SET AEXERCISE - ACHIEVERS SECTION5videos
IMO QUESTION PAPER 2018 SET A
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 1EXERCISE - Achievers Section5videos
IMO QUESTION PAPER 2020 SET 1
Similar Questions
In A PQR, if PQ=PQ and L, M and N are the mid-points of the sides PQ, PR and RP respectively. Prove that LN=MN
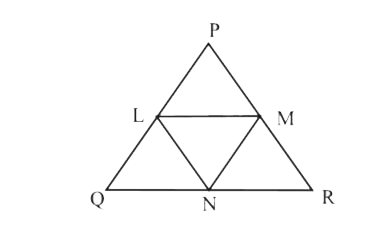
View SolutionIn the given figure L, M and N are mid point of the sides PQ, PR and QR respectively of ΔPQR. If PQ = 4.4 cm, QR = 5.6 cm and PR = 4.8 cm then find the perimeter of ΔLMN.
View Solution
Knowledge Check
- Question 1 - Select One
In a square PQRS, X and Y are mid points of sides PS and QR respectively. XY and QS intersect a t O. Find the area of ΔXOS, if PQ = 8 cm.
A6 cm2B12 cm2C4 cm2D8 cm2
M and N are mid- point on sides QR and PQ respectively of △PQR, right-anggled at Q. Prove that :
PM2+RN2=5MN2.View SolutionLet ABC be a triangle with circumcenre O. The points P and Q are interior points of the sides Let K, L and M be the mid points of the segments BP, CQ and PQ respectively, and let τ be the circle passing through K, L and M. Suppose that the line PQ is tangent to the circle τ. Prove that OP=OQ.
View SolutionIn the given figure, the two lines AB and CD intersect at a point O such that ∠BOC=125∘. Find the values of x, y, and z.
View SolutionIn ΔPQR,Pq=PR and S is the mid-point of PQ. A line drawn from S parallel to QR, intersects the line PR at T. Prove that PS = PT.
View SolutionIn ΔPQR,Pq=PR and S is the mid-point of PQ. A line drawn from S parallel to QR, intersects the line PR at T. Prove that PS = PT.
View Solution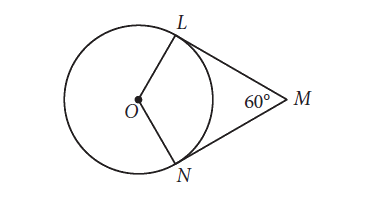
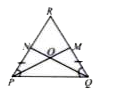
In the figure above, point O is the center of the circle, line segments LM and MN are tangent to the circle at points L and N, respectively, and the segments intersect at point M as shown. If the circumference of the circle is 96, what is the length of minor arc ⌢LN ?View SolutionIn the figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR such that QM = PN. Prove that OP=OQ, where O is the point of intersection of PM and QN.
View Solution