Let ABC be a triangle with circumcenre O. The points P and Q are interior points of the sides Let K, L and M be the mid points of the segments BP, CQ and PQ respectively, and let τ be the circle passing through K, L and M. Suppose that the line PQ is tangent to the circle τ. Prove that OP=OQ.
Step by step video & image solution for Let ABC be a triangle with circumcenre O. The points P and Q are interior points of the sides Let K, L and M be the mid points of the segments BP, CQ and PQ respectively, and let tau be the circle passing through K, L and M. Suppose that the line PQ is tangent to the circle tau. Prove that OP=OQ. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Let □PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=
A3¯¯¯¯¯¯¯¯MNB4¯¯¯¯¯¯¯¯MNC2¯¯¯¯¯¯¯¯MND2¯¯¯¯¯¯¯¯NMLet P be an interior point of a triangle ABC , Let Q and R be the reflections of P in AB and AC , respectively if Q .A , R are collinear then ∠A equals -
A30∘B60∘C90∘D120∘Let P be the point (1,0) and Q a point on the locus y2=8x. The locus of mid-point of PQ is :
AP1 lies on C2andQ1 lies on C1BPQ≥min{PP1,QQ1}Cpoint P0 on C1 such that P0Q0≤PQ for all pairs of points (P,Q) is (13,109)Dpoint Q0 on C2 such that P0Q0≤PQ for all pairs of points (P,Q) is (109,13)
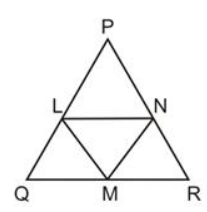
In ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.

View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
View SolutionPoint O is the centre of a circle . Line a and line b are parallel tangents to the circle at P and Q. Prove that segment PQ is a diameter of the circle.

View SolutionIn Figure, lIIm and M is the mid-point of the line segment AB. Prove that M is also the mid-point of any line segment CD having its end-points on l and m respectively.
View SolutionLet P and Q be the points on the line joining A(−2,5) and B(3, 1) such that AP=PQ=QB. Then, the mid-point of PQ is
View Solution