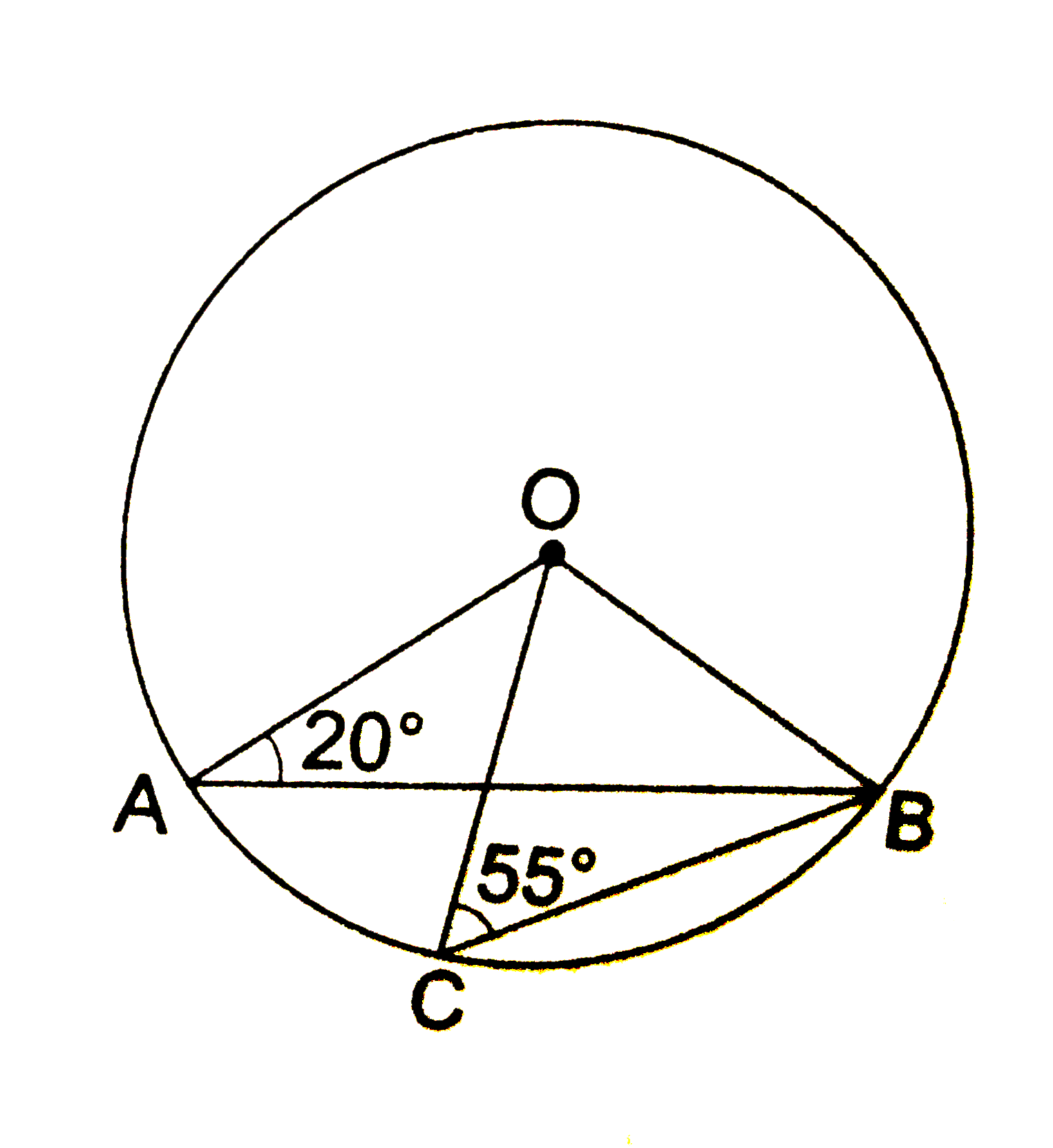
In the given figure, O is the centre of a circle in which ∠OAB=20∘ and ∠OCB=55∘. Find (i)∠BOC,(ii)∠AOC.
Video Solution
Text Solution
The correct Answer is:(i)∠BOC=70∘ (ii)∠AOC=70∘
OB=OC⇒∠OBC=∠OCB=55∘
∴∠BOC=180∘−(∠OCB+∠OBC)
=[180∘−(55∘+55∘)]=70∘
OA=OB⇒∠OBA=∠OAB=20∘
⇒∠OAB=180∘−(∠OAB+∠OBA)
⇒∠AOB=180∘−(20∘+20∘)=140∘
∴∠AOC=∠AOB−∠BOC=140∘=70∘=70∘
|
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12C
26 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)
5 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
In the given figure, O is the centre of the circle. The value of x is
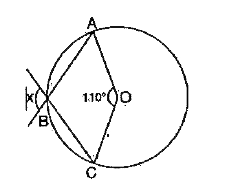 A75∘B55∘C125∘D110∘
A75∘B55∘C125∘D110∘In the given figure, O is the centre of circle. ∠AOC=120∘. Find ∠BAC :
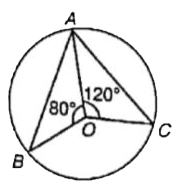 A120∘B80∘C100∘Dnone of the above
A120∘B80∘C100∘Dnone of the aboveIn the given figure, O is the centre of the circle. ∠AOB=70∘, find ∠OCD :
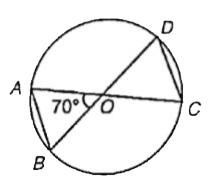 A70∘B55∘C65∘D110∘
A70∘B55∘C65∘D110∘
In the given figure,O is the centre of the circle ∠OAB=30∘ and ∠OCB=40∘. Calculate ∠AOC
View SolutionIn the given figure, O is the centre of the circle∠AOB=90∘ Find m∠APB
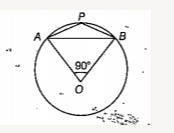
View SolutionIn the given figure, if O is centre of circle, then ∠PQR=
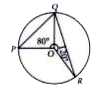
View SolutionIn the given figure, O is the centre of the circle and ∠ACB=25∘ Find ∠AOB
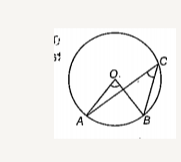
View SolutionIn the given figure, O is the centre of circle, ∠AOB=100∘. Find ∠BCD :
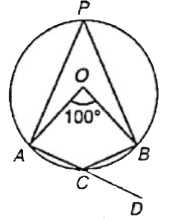
View Solution
